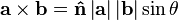理解点线拓扑关系的计算原理

前序

由于业务需要，我学习了判断点与点、点与线、线与线的关系的算法、理论，这里汇总下，主要内容有：

1. 点与点的关系
2. 点与线的关系
3. 线与线的关系

 

点与点

点与点关系相对最简单，使用勾股定理即可：

这是怎样计算两个已知坐标点之间的距离：

 

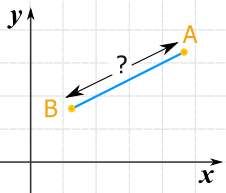
把两点名为 A 和 B

 

 

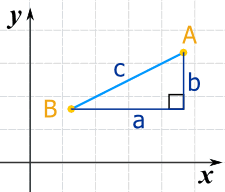
我们用从 A 画的垂直线和从 B 画的水平线，形成一个直角三角形。

勾股定理告诉我们：

a² + b² = c²

 

 

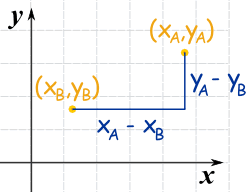
标出 A 和 B的坐标。

x_A 代表 A 的 x坐标
y_A 代表 A 的 y坐标

水平距离 a 是 (x_A − x_B)

垂直距离 b 是 (y_A − y_B)

 

我们现在可以解 c (两点之间的距离）：

开始：		c2 = a2 + b2
代进 a 和 b 的式：		c2 = (xA − xB)2 + (yA − yB)2
结果：

 

 

点与线的关系

这里分为：

点到线的最短距离，也叫点线距离或垂线长度， 这个不是今天的重点，细节移步到此。

点在线的方位：在左侧还是右侧？

这里不得不先讲个东西：点乘， 也被称为“点积”、“标量积“、”内积“

对于向量a和向量b：                                                 

a和b的点积公式为：

其中一维向量a和向量b的行列数相同。

点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影，有公式：

 

推导过程如下，首先看一下向量组成：

 

 

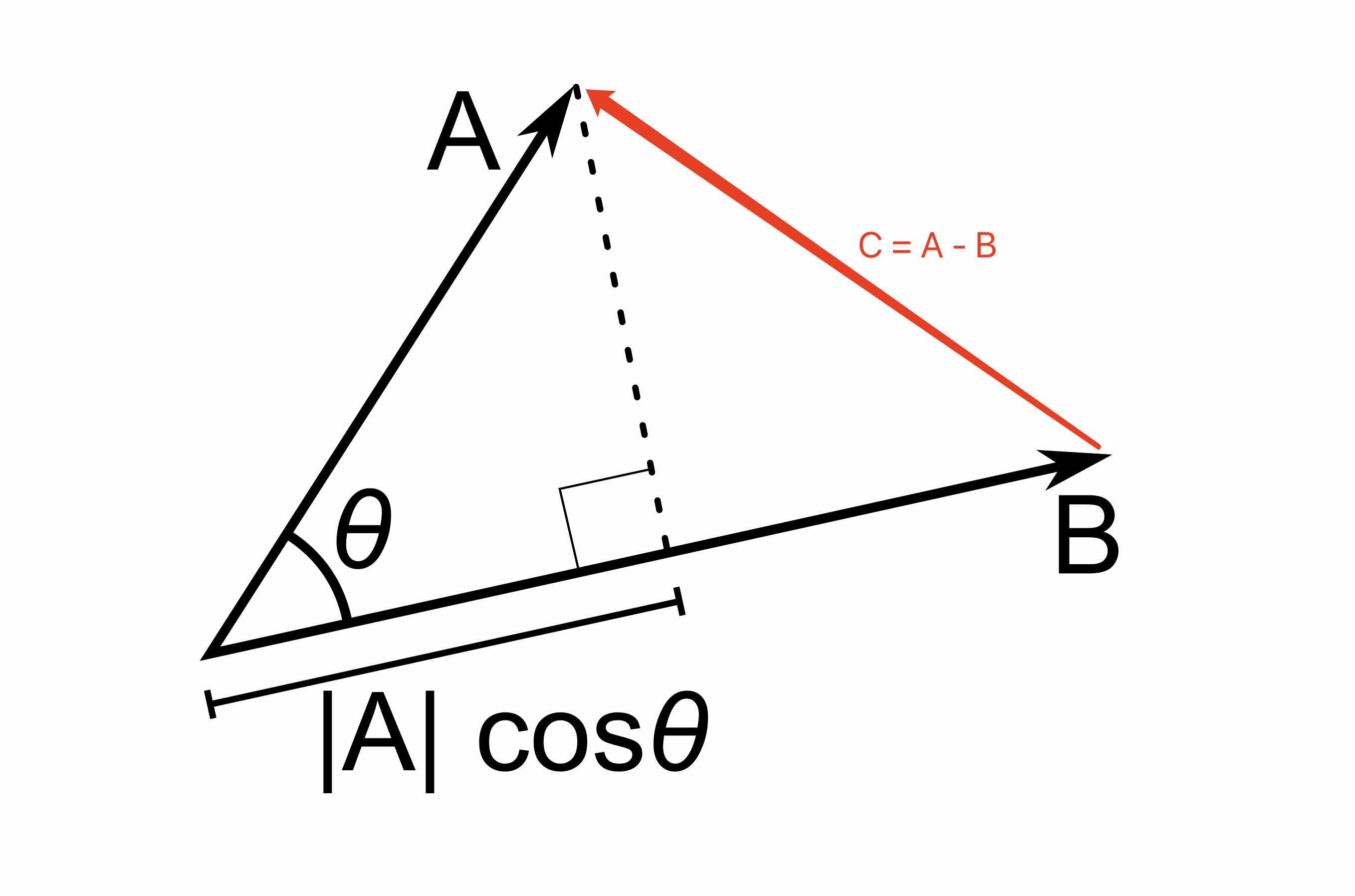
定义向量：

 

 

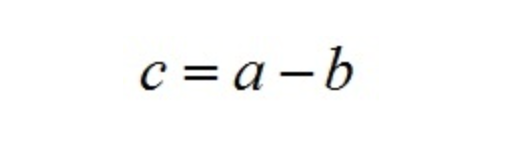
根据三角形余弦定理有：

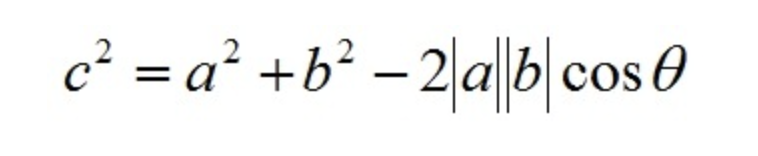
根据关系c=a-b（a、b、c均为向量）有：

即：

 

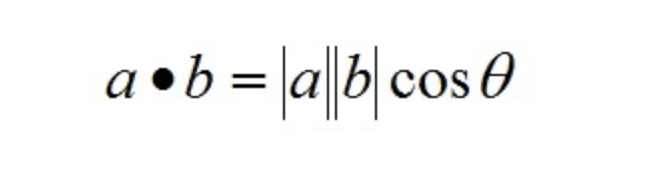
向量a，b的长度都是可以计算的已知量，从而有a和b间的夹角θ：

 

 

根据这个公式就可以计算向量a和向量b之间的夹角。从而就可以进一步判断这两个向量是否是同一方向，是否正交(也就是垂直)等方向关系，具体对应关系为：

     a·b>0    方向基本相同，夹角在0°到90°之间

     a·b=0    正交，相互垂直  

     a·b<0    方向基本相反，夹角在90°到180°之间 

这样就能判断点在直线哪边。

 

线与线的关系

常用问题：

线与线是否相交？

判断两条线段是否相交有两步：
①快速排斥计算
②跨立计算

快速排斥
给出线条AB、CD，如果以AB、CD为对角线的矩形不相交，那么AB、CD也必不可能相交；如果矩形相交，那么需要再通过跨立计算进行判断。对于矩形不相交，有下面两种情况：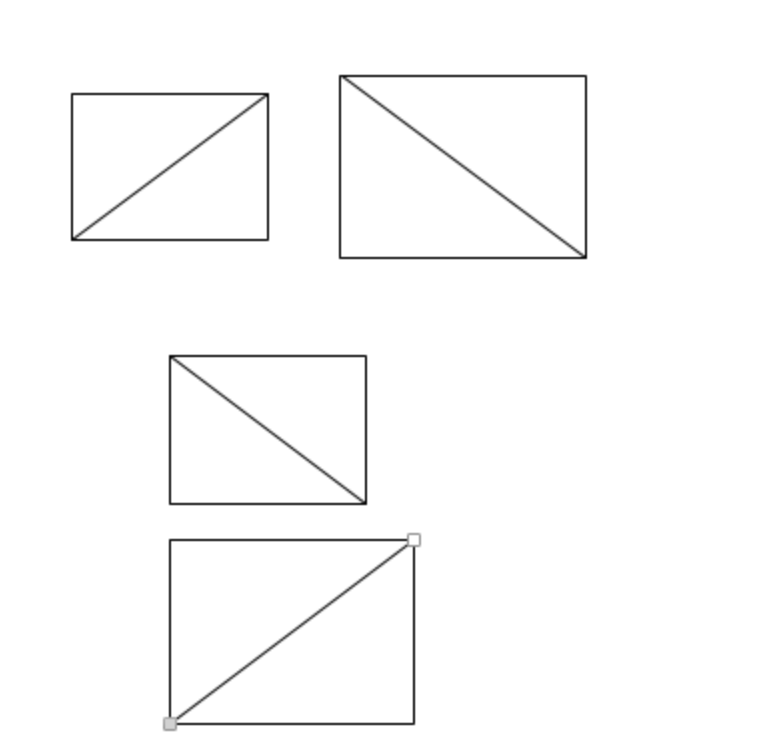

对于上面两种情况，可以分成四类来讨论：
①AB两坐标中最大的x值 小于 CD两坐标中最小x值
②CD两坐标中最大的x值 小于 AB两坐标中最小x值
③AB两坐标中最大的y值 小于 CD两坐标中最小y值
④CD两坐标中最大的y值 小于 AB两坐标中最小y值

只要满足了以上四种的其中一种，就可以认为AB与CD不相交。

跨立计算：

首先，这里需要用到向量叉乘的算法：其中AB与CD是三维空间上的向量，与xOy平面平行。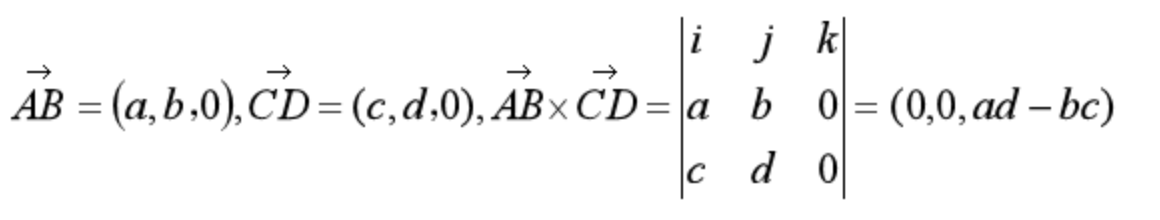

其次，如下图。AB与CD相交必然有A、B在线段CD两边，C、D在线段AB两边。
根据上面的公式和右手螺旋法则：

左边是“左手法则”， 右边是“右手法则”, 用手表示为下图：

 

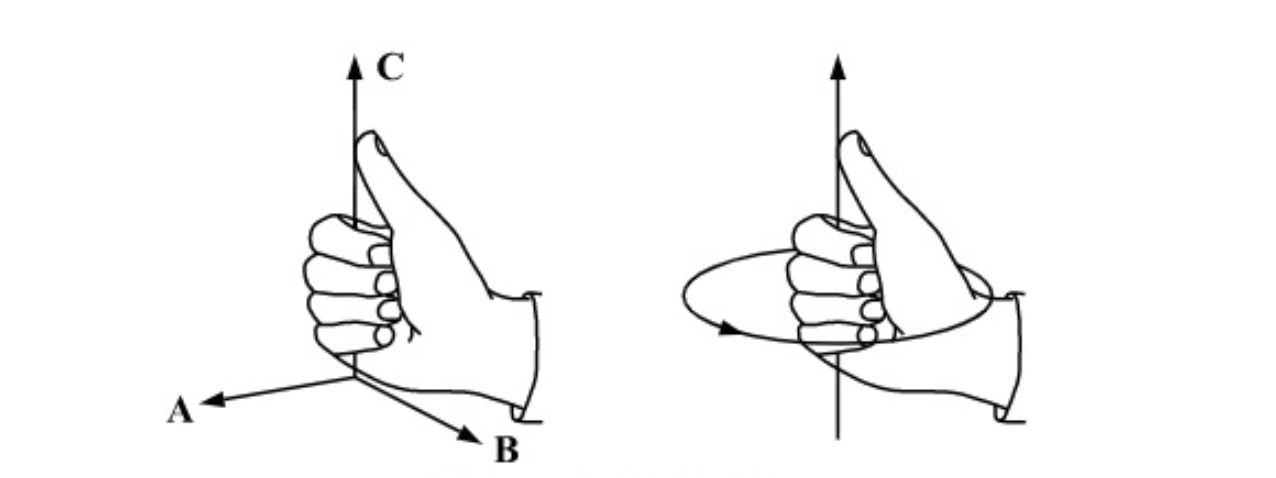
如果相交，AB X AC的z坐标值z1与AB X AD的z坐标值z2必然异号；同样的，DC X DA的z坐标值z3与DC X DB的z坐标值z4也必然异号。

两个向量a和b的叉积写作a × b（有时也被写成a ∧ b，避免和字母x混淆）。叉积可以被定义为：

在这里θ表示a和b之间的角度（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。而n是一个与a和b均垂直的单位矢量。

特别的，如果B在CD上时，求得的z坐标值是0。所以只要同时满足z1 X z2 ≤ 0，z3 X z4 ≤ 0，就能保证必然相交。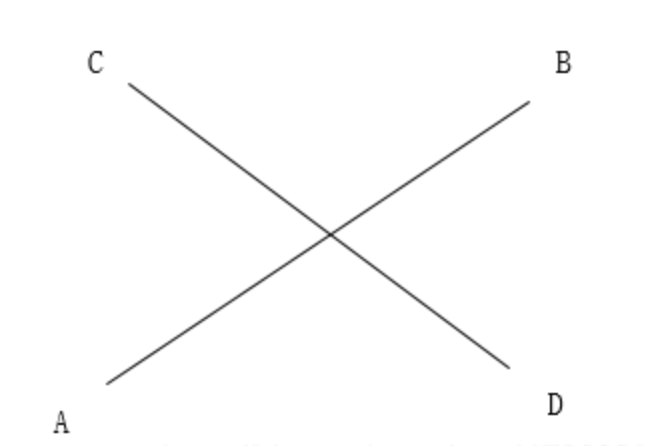

参考代码（Go）

type Point struct {
	X float64
	Y float64
}

type Segment struct {
	A Point
	B Point
}


// IsSegmentsIntersect 2个线段是否相交
func IsSegmentsIntersect(line1 Segment, line2 Segment, containsEnds bool) bool {
   //判断矩形相交
   if math.Min(line1.A.X, line1.B.X) > math.Max(line2.A.X, line2.B.X) ||
      math.Max(line1.A.X, line1.B.X) < math.Min(line2.A.X, line2.B.X) ||
      math.Min(line1.A.Y, line1.B.Y) > math.Max(line2.A.Y, line2.B.Y) ||
      math.Max(line1.A.Y, line1.B.Y) < math.Min(line2.A.Y, line2.B.Y) {
      return false
   }
   //判断点的位置：如果任意线段的2个端点在另一条线的两侧，则两线相交
   a1 := IsPointOnLine(line1.A, line2)
   b1 := IsPointOnLine(line1.B, line2)
   a2 := IsPointOnLine(line2.A, line1)
   b2 := IsPointOnLine(line2.B, line1)

   // a*b < 0表示2个端点在另一条线的两端
   x1 := a1 * b1
   x2 := a2 * b2
   if containsEnds && (x1 == 0 || x2 == 0) {
      return true
   }
   isCross := a1*b1 < 0 && a2*b2 < 0
   return isCross
}
// IsPointOnLine 判断点是否在线段上, 返回值 > 0 在右侧, = 0 在线上, < 0 在左侧
func IsPointOnLine(p Point, s Segment) float64 {
	return (s.B.Y-p.Y)*(s.A.X-p.X) - (s.A.Y-p.Y)*(s.B.X-p.X)
}