玩透二叉树(Binary-Tree)及前序（先序）、中序、后序【递归和非递归】遍历
基础预热：
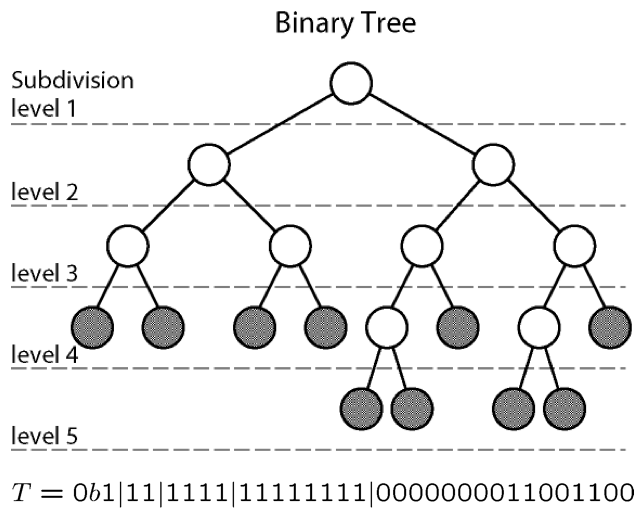
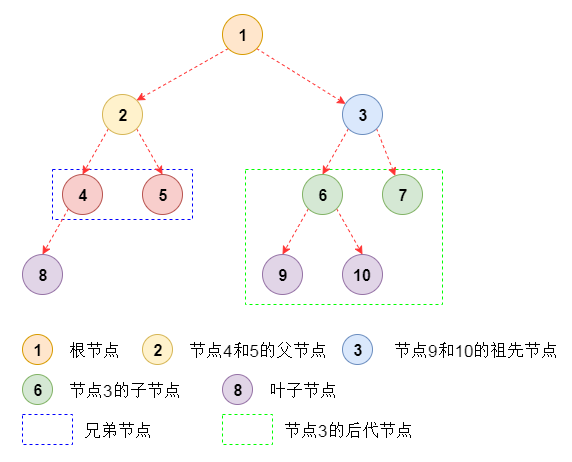
结点的度（Degree）：结点的子树个数；
树的度：树的所有结点中最大的度数；
叶结点（Leaf）：度为0的结点；
父结点（Parent）：有子树的结点是其子树的根节点的父结点；
子结点/孩子结点（Child）：若A结点是B结点的父结点，则称B结点是A结点的子结点；
兄弟结点（Sibling）：具有同一个父结点的各结点彼此是兄弟结点；
路径和路径长度：从结点n1到nk的路径为一个结点序列n1，n2，…，nk。ni是ni+1的父结点。路径所包含边的个数为路径的长度；
祖先结点（Ancestor）：沿树根到某一结点路径上的所有结点都是这个结点的祖先结点；
子孙结点（Descendant）：某一结点的子树中的所有结点是这个结点的子孙；
结点的层次（Level）：规定根结点在1层，其他任一结点的层数是其父结点的层数加1；
树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度；
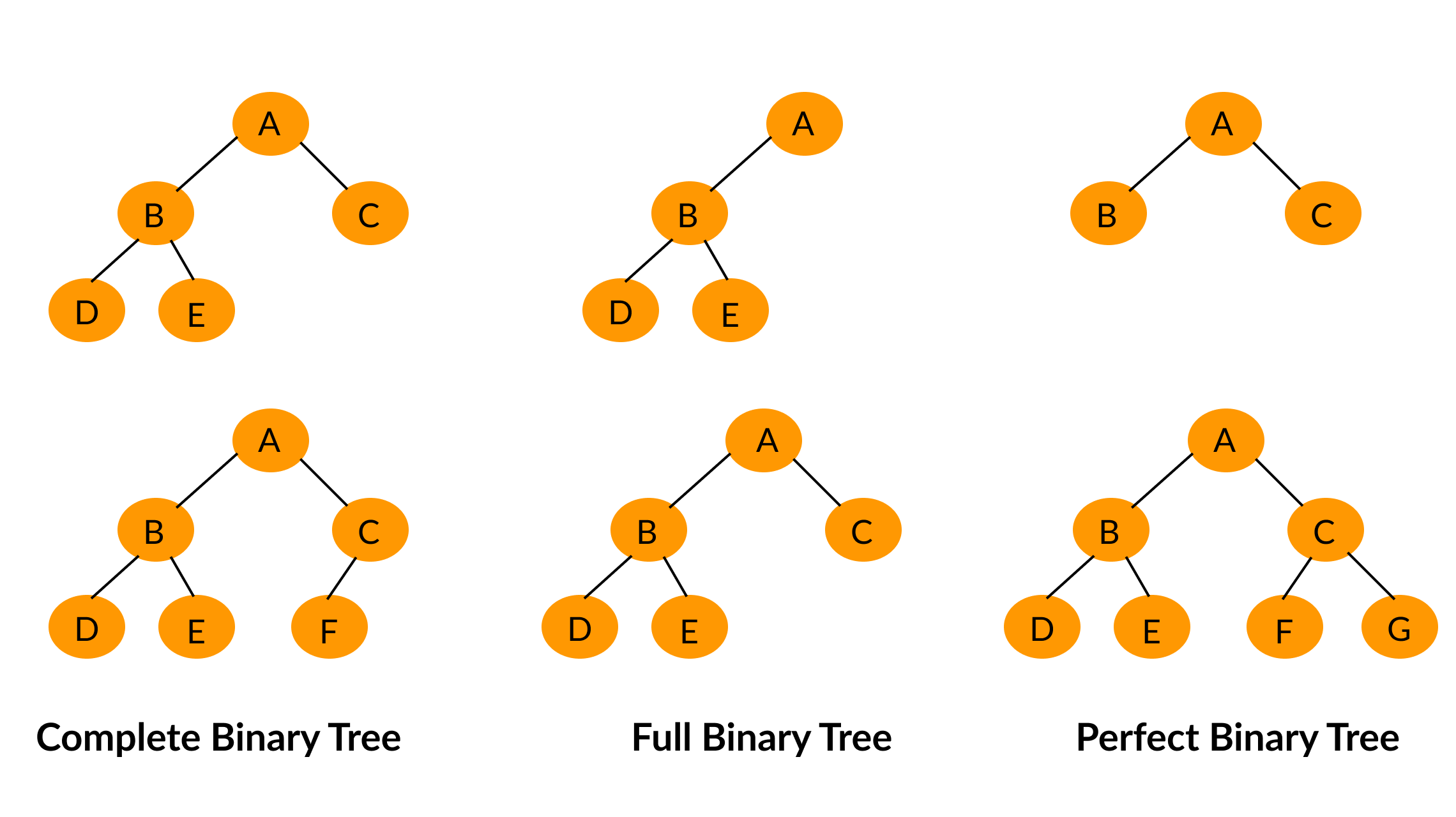
满二叉树
除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树。
完全二叉树
一棵二叉树至多只有最下面的一层上的结点的度数可以小于2，并且最下层上的结点都集中在该层最左边的若干位置上，则此二叉树成为完全二叉树。
平衡二叉树
它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树
前序、中序、后序
首先给出二叉树节点类：
树节点：
class TreeNode {
int val;
//左子树
TreeNode left;
//右子树
TreeNode right;
//构造方法
TreeNode(int x) {
val = x;
}
}
无论是哪种遍历方法，考查节点的顺序都是一样的(思考做试卷的时候，人工遍历考查顺序)。只不过有时候考查了节点，将其暂存，需要之后的过程中输出。
如图1所示，三种遍历方法(人工)得到的结果分别是：
先序：1 2 4 6 7 8 3 5
中序：4 7 6 8 2 1 3 5
后序：7 8 6 4 2 5 3 1
三种遍历方法的考查顺序一致，得到的结果却不一样，原因在于：
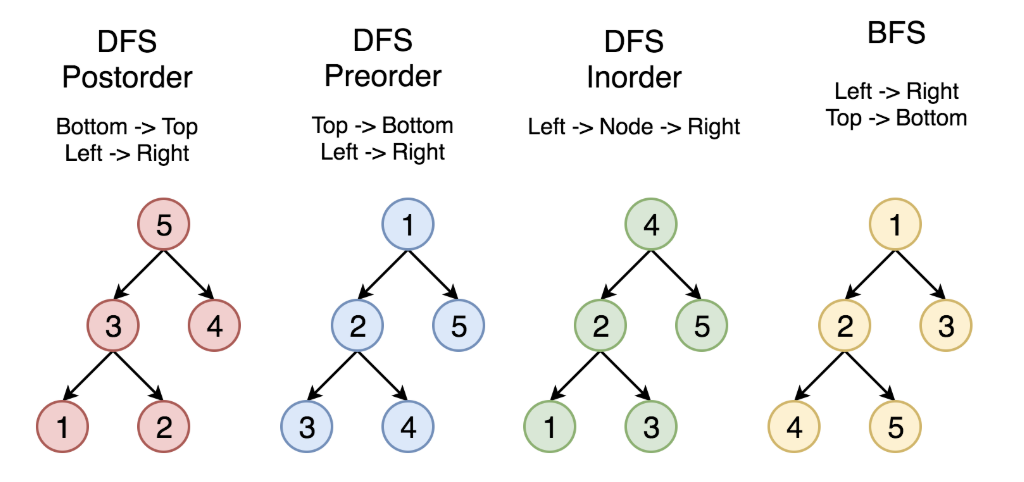
先序：考察到一个节点后，即刻输出该节点的值，并继续遍历其左右子树。(根左右)
中序：考察到一个节点后，将其暂存，遍历完左子树后，再输出该节点的值，然后遍历右子树。(左根右)
后序：考察到一个节点后，将其暂存，遍历完左右子树后，再输出该节点的值。(左右根)
先序遍历
递归先序遍历
递归先序遍历很容易理解，先输出节点的值，再递归遍历左右子树。中序和后序的递归类似，改变根节点输出位置即可。
// 递归先序遍历
public static void recursionPreorderTraversal(TreeNode root) {
if (root != null) {
System.out.print(root.val + " ");
recursionPreorderTraversal(root.left);
recursionPreorderTraversal(root.right);
}
}
非递归先序遍历
因为要在遍历完节点的左子树后接着遍历节点的右子树，为了能找到该节点，需要使用栈来进行暂存。中序和后序也都涉及到回溯，所以都需要用到栈。
遍历过程参考注释
// 非递归先序遍历
public static void preorderTraversal(TreeNode root) {
// 用来暂存节点的栈
Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
// 新建一个游标节点为根节点
TreeNode node = root;
// 当遍历到最后一个节点的时候，无论它的左右子树都为空，并且栈也为空
// 所以，只要不同时满足这两点，都需要进入循环
while (node != null || !treeNodeStack.isEmpty()) {
// 若当前考查节点非空，则输出该节点的值
// 由考查顺序得知，需要一直往左走
while (node != null) {
System.out.print(node.val + " ");
// 为了之后能找到该节点的右子树，暂存该节点
treeNodeStack.push(node);
node = node.left;
}
// 一直到左子树为空，则开始考虑右子树
// 如果栈已空，就不需要再考虑
// 弹出栈顶元素，将游标等于该节点的右子树
if (!treeNodeStack.isEmpty()) {
node = treeNodeStack.pop();
node = node.right;
}
}
}
先序遍历结果：
递归先序遍历： 1 2 4 6 7 8 3 5
非递归先序遍历：1 2 4 6 7 8 3 5
中序遍历
递归中序遍历
过程和递归先序遍历类似
// 递归中序遍历
public static void recursionMiddleorderTraversal(TreeNode root) {
if (root != null) {
recursionMiddleorderTraversal(root.left);
System.out.print(root.val + " ");
recursionMiddleorderTraversal(root.right);
}
}
非递归中序遍历
和非递归先序遍历类似，唯一区别是考查到当前节点时，并不直接输出该节点。
而是当考查节点为空时，从栈中弹出的时候再进行输出(永远先考虑左子树，直到左子树为空才访问根节点)。
// 非递归中序遍历
public static void middleorderTraversal(TreeNode root) {
Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
TreeNode node = root;
while (node != null || !treeNodeStack.isEmpty()) {
while (node != null) {
treeNodeStack.push(node);
node = node.left;
}
if (!treeNodeStack.isEmpty()) {
node = treeNodeStack.pop();
System.out.print(node.val + " ");
node = node.right;
}
}
}
中序遍历结果
递归中序遍历： 4 7 6 8 2 1 3 5
非递归中序遍历：4 7 6 8 2 1 3 5
后序遍历
递归后序遍历
过程和递归先序遍历类似
// 递归后序遍历
public static void recursionPostorderTraversal(TreeNode root) {
if (root != null) {
recursionPostorderTraversal(root.left);
recursionPostorderTraversal(root.right);
System.out.print(root.val + " ");
}
}
非递归后序遍历
后续遍历和先序、中序遍历不太一样。
后序遍历在决定是否可以输出当前节点的值的时候，需要考虑其左右子树是否都已经遍历完成。
所以需要设置一个lastVisit游标。
若lastVisit等于当前考查节点的右子树，表示该节点的左右子树都已经遍历完成，则可以输出当前节点。
并把lastVisit节点设置成当前节点，将当前游标节点node设置为空，下一轮就可以访问栈顶元素。
否者，需要接着考虑右子树，node = node.right。
以下考虑后序遍历中的三种情况：
如图3所示，从节点1开始考查直到节点4的左子树为空。
注：此时的游标节点node = 4.left == null。
此时需要从栈中查看 Peek()栈顶元素。
发现节点4的右子树非空，需要接着考查右子树，4不能输出，node = node.right。
如图4所示，考查到节点7(7.left == null，7是从栈中弹出)，其左右子树都为空，可以直接输出7。
此时需要把lastVisit设置成节点7，并把游标节点node设置成null，下一轮循环的时候会考查栈中的节点6。
如图5所示，考查完节点8之后(lastVisit == 节点8)，将游标节点node赋值为栈顶元素6，节点6的右子树正好等于节点8。表示节点6的左右子树都已经遍历完成，直接输出6。
此时，可以将节点直接从栈中弹出Pop()，之前用的只是Peek()。
将游标节点node设置成null。
// 非递归后序遍历
public static void postorderTraversal(TreeNode root) {
Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
TreeNode node = root;
TreeNode lastVisit = root;
while (node != null || !treeNodeStack.isEmpty()) {
while (node != null) {
treeNodeStack.push(node);
node = node.left;
}
//查看当前栈顶元素
node = treeNodeStack.peek();
//如果其右子树也为空，或者右子树已经访问
//则可以直接输出当前节点的值
if (node.right == null || node.right == lastVisit) {
System.out.print(node.val + " ");
treeNodeStack.pop();
lastVisit = node;
node = null;
} else {
//否则，继续遍历右子树
node = node.right;
}
}
}
后序遍历结果
递归后序遍历： 7 8 6 4 2 5 3 1
非递归后序遍历：7 8 6 4 2 5 3 1
完整算法、用例 by Golang
package main import "fmt" type Node struct { V int L *Node R *Node } //前序 func forwardLook(root *Node) { if root == nil { return } //输出行的位置在最前面 fmt.Printf("node %v ", root.V) forwardLook(root.L) forwardLook(root.R) } //var i int func forwardLoop(root *Node) { //需要一个堆保存走过的路径 nodes:=[]*Node{} for len(nodes) != 0 || root != nil { //一直往左走 for root != nil{ nodes=append(nodes, root) fmt.Printf("node %v ",root.V) root = root.L } //说明左子结点为空，那么就看右结点 if len(nodes) >0 { root=nodes[len(nodes)-1] //用完最近一个结点后，删除它，删除后最后的结点一定是父结点 nodes=nodes[:len(nodes)-1] //左子结点遍历完了，所以这里只看当看结点的右子结点 root=root.R }else{ root = nil } } } //中序 func middleLook(root *Node) { if root == nil { return } middleLook(root.L) //输出行的位置在中间 fmt.Printf("node %v ", root.V) middleLook(root.R) } //后序 func backwardLook(root *Node) { if root == nil { return } //输出行的位置在后面 backwardLook(root.L) backwardLook(root.R) fmt.Printf("node %v ", root.V) } func main(){ tree:=&Node{1, &Node{2, &Node{4, nil, nil}, &Node{5, nil, nil}, }, &Node{3, &Node{6, nil, nil}, &Node{7, nil, nil}, }, } fmt.Println("\nforwardLook ") forwardLook(tree) fmt.Println("\nforwardLoop ") forwardLoop(tree) fmt.Println("\nmiddleLook ") middleLook(tree) fmt.Println("\nbackwardLook ") backwardLook(tree) tree=&Node{1, &Node{2, nil, &Node{4, nil, &Node{6, &Node{7, nil, nil}, &Node{8, nil, nil}, }, }, }, &Node{3, nil, &Node{5, nil, nil}, }, } fmt.Println("\nforwardLook ") forwardLook(tree) fmt.Println("\nforwardLoop ") forwardLoop(tree) fmt.Println("\nmiddleLook ") middleLook(tree) fmt.Println("\nbackwardLook ") backwardLook(tree) }
总结
本文来自博客园，作者：sunsky303，转载请注明原文链接：https://www.cnblogs.com/sunsky303/p/11733209.html
