十二种排序包你满意(冒泡、插入、归并、快速排序等包含希尔和计数排序)
前言
排序算法在计算机科学入门课程中很普遍,在学习排序算法的时候,涉及到大量的各种核心算法概念,例如大O表示法,分治法,堆和二叉树之类的数据结构,随机算法,最佳、最差和平均情况分析,时空权衡以及上限和下限,本文就介绍了十二种排序算法供大家学习。
简介
排序算法是用来根据元素对应的比较运算符重新排列给定的数组的算法,输出的数组是一个根据比较符从小到大或者从大到小依次排列的数组。比较运算符是用于确定相应数据结构中元素的新顺序,比如在整数数组里面,对应的比较符号就是大于或者小于号,用户也可以自己定义对应的比较运算符。
比如如果输入是[4,2,3,1],按照从小到大输出,结果应该是[1,2,3,4]
特性
稳定性
如果在数组中有两个元素是相等的,在经过某个排序算法之后,原来在前面的的那个元素仍然在另一个元素的前面,那么我们就说这个排序算法是稳定的。
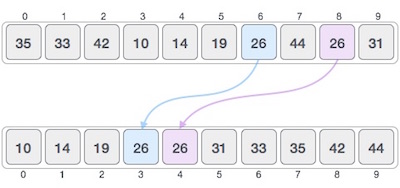
如果在排序之后,原来的两个相等元素中在前面的一个元素被移到了后面,那么这个算法就是不稳定的。
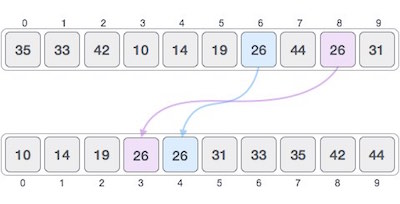
比如排序之前数组为[3(a),2,3(b)](其中a和b分别代表两个不同的3),经过某个排序算法之后是[2,3(a),3(b)],那么这个算法就是稳定的;如果变成了[2,3(b),3(a)],那么这个算法是不稳定的。
再比如在按照身高排队去食堂打饭的过程中,小明和小刚的身高都是170,原来小明在小刚前面,但是经过排序之后小明发现小刚到了他前面了,这样小明肯定对这个不稳定的排序有意见。
时间复杂度
时间复杂度反映了算法的排序效率,通常用大O表示法来表示,通常暗示这个算法需要的最多操作次数的量级,比如表示最多需要进行量级操作。
空间复杂度
空间复杂度反映了算法需要消耗的空间,比如表示只需要常数量级的空间,不会随着数组大小的变化而变化。
如果一个排序算法不需要额外的存储空间,可以直接在原来的数组完成排序操作,这个算法可以被称之为原地算法,空间复杂度是
比较排序、非比较排序
如果一个算法需要在排序的过程中使用比较操作来判断两个元素的大小关系,那么这个排序算法就是比较排序,大部分排序算法都是比较排序,比如冒泡排序、插入排序、堆排序等等,这种排序算法的平均时间复杂度最快也只能是。
非比较排序比较典型的有计数排序、桶排序和基数排序,这类排序能够脱离比较排序时间复杂度的束缚,达到级别的效率。
算法
首先定义基本的交换数组元素的基本方法,节省后面的代码量。
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
冒泡排序
冒泡排序是从左到右依次比较相邻的两个元素,如果前一个元素比较大,就把前一个元素和后一个交换位置,遍历数组之后保证最后一个元素相对于前面的永远是最大的。然后让最后一个保持不变,重新遍历前n-1个元素,保证第n-1个元素在前n-1个元素里面是最大的。依此规律直到第2个元素是前2个元素里面最大的,排序就结束了。
因为这个排序的过程很像冒泡泡,找到最大的元素不停的移动到最后端,所以这个排序算法就叫冒泡排序。
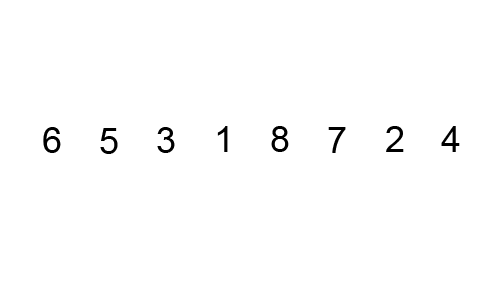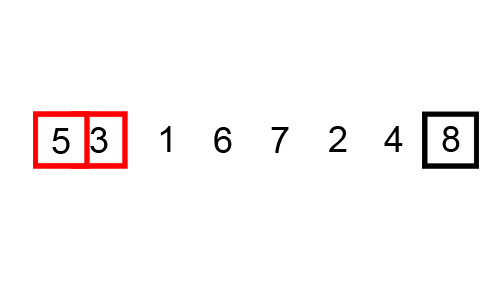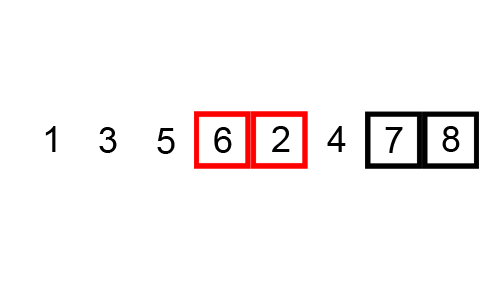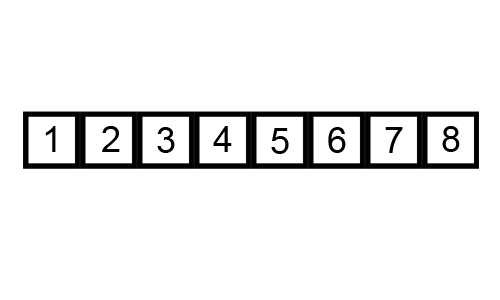
图片来自这里
用Java代码实现
private void bubbleSort(int[] nums) {
for (int i = nums.length - 1; i >= 1; i--) { // 冒泡得到n-1个最大值
for (int j = 1; j <= i; j++) {
if (nums[j-1]>nums[j])
swap(nums, j, j-1); // 交换得到较大值
}
}
}
冒泡排序的最大特点就是代码简单,短短的五行代码就能完成整个排序的操作。
时间复杂度比较稳定不管怎样都需要次比较,所以是的时间复杂度。
空间复杂度是,所有操作在原来的数组完成就可以了,不需要额外的空间。
算法是稳定的,在冒泡的过程中如果两个元素相等,那么他们的位置是不会交换的。
选择排序
选择排序的思路比较简单,先找到前n个元素中最大的值,然后和最后一个元素交换,这样保证最后一个元素一定是最大的,然后找到前n-1个元素中的最大值,和第n-1个元素进行交换,然后找到前n-2个元素中最大值,和第n-2个元素交换,依次类推到第2个元素,这样就得到了最后的排序数组。
其实整个过程和冒泡排序差不多,都是要找到最大的元素放到最后,不同点是冒泡排序是不停的交换元素,而选择排序只需要在每一轮交换一次。

原图来自这里
代码实现:
private void selectionSort(int[] nums) {
for (int i = nums.length - 1; i > 0; i--) {
int maxIndex = 0; // 最大元素的位置
for (int j = 0; j <= i; j++) {
if (nums[maxIndex]<nums[j]) {
maxIndex = j;
}
}
swap(nums, maxIndex, i); // 把这个最大的元素移到最后
}
}
时间复杂度和冒泡排序一样比较稳定,都需要次比较,所以时间复杂度是
空间复杂度是,不需要额外空间,是原地算法。
选择排序最简单的版本是不稳定的,比如数组[1,3,2,2],表示为[1,3,2(a),2(b)],在经过一轮遍历之后变成了[1,2(b),2(a),3],两个2之间的顺序因为第一个2和3的调换而颠倒了,所以不是稳定排序。
不过可以改进一下选择排序变成稳定的。原来不稳定是因为交换位置导致的,现在如果改成插入操作(不是使用数组而是链表,把最大的元素插入到最后)的话,就能变成稳定排序。比如[1,3,2(a),2(b)],在第一轮中变成了[1,2(a),2(b),3],这样就能够保持相对位置,变成稳定排序。
插入排序
插入排序的核心思想是遍历整个数组,保持当前元素左侧始终是排序后的数组,然后将当前元素插入到前面排序完成的数组的对应的位置,使其保持排序状态。有点动态规划的感觉,类似于先把前i-1个元素排序完成,再插入第i个元素,构成i个元素的有序数组。

图片来自这里
简单代码实现:
private void insertionSort(int[] nums) {
for (int i = 1; i < nums.length; i++) { // 从第二个元素开始遍历
int j = i;
while (j>0&&nums[j]<nums[j-1]) { // 将当前元素移动到合适的位置
swap(nums, j, j-1);
j--;
}
}
}
时间复杂度上,插入排序在最好的情况,也就是数组已经排好序的时候,复杂度是,在其他情况下都是。
空间复杂度是,不需要额外的空间,是原地算法。
插入排序是稳定排序,每次交换都是相邻元素的交换,不会有选择排序的那种跳跃式交换元素。
希尔排序
希尔排序可以看作是一个冒泡排序或者插入排序的变形。希尔排序在每次的排序的时候都把数组拆分成若干个序列,一个序列的相邻的元素索引相隔的固定的距离gap,每一轮对这些序列进行冒泡或者插入排序,然后再缩小gap得到新的序列一一排序,直到gap为1
比如对于数组[5,2,4,3,1,2],第一轮gap=3拆分成[5,3]、[2,1]和[4,2]三个数组进行插入排序得到[3,1,2,5,2,4];第二轮gap=2,拆分成[3,2,2]和[1,5,4]进行插入排序得到[2,1,2,4,3,5];最后gap=1,全局插入排序得到[1,2,2,3,4,5]
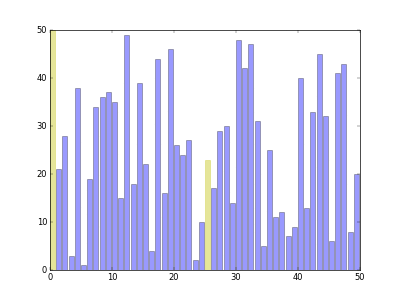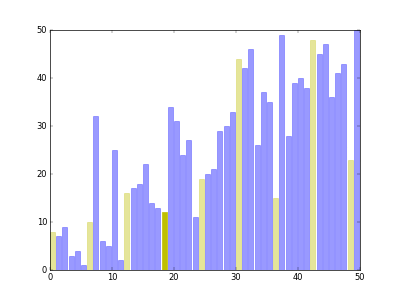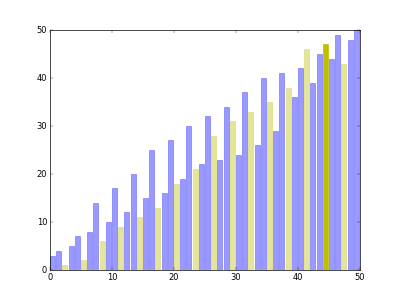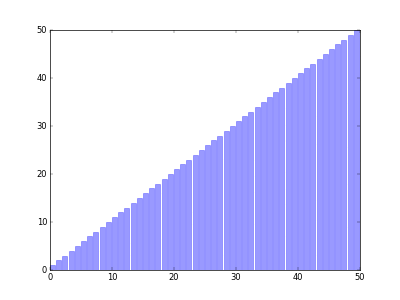
图片来自这里
简单代码实现:
private void shellSor(int[] nums) {
int gap = nums.length >> 1;
while (gap > 0) {
for (int i = 0; i < gap; i++) { // 对每个子序列进行排序
for (int j = i+gap; j < nums.length; j+=gap) { // 插入排序的部分
int temp = j;
while (temp > i && nums[temp] < nums[temp-gap]) {
swap(nums, temp, temp-gap);
temp -= gap;
}
}
}
gap >>= 1;
}
}
Donald Shell于1959年发布了这种排序算法,运行时间在很大程度上取决于它使用的间隔,在实际使用中,其时间复杂度仍然是一个悬而未决的问题,基本在和之间。
空间复杂度是,是原地算法。
这个算法是不稳定的,里面有很多不相邻元素的交换操作。
归并排序
归并排序是典型的使用分治思想(divide-and-conquer)解决问题的案例。在排序的过程中,把原来的数组变成左右两个数组,然后分别进行排序,当左右的子数组排序完毕之后,再合并这两个子数组形成一个新的排序数组。整个过程递归进行,当只剩下一个元素或者没有元素的时候就直接返回。
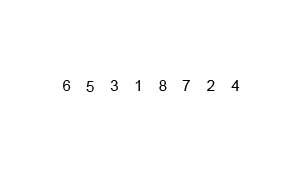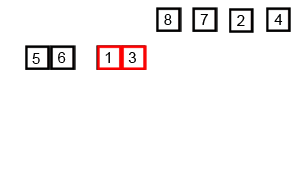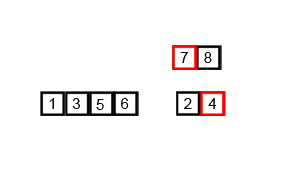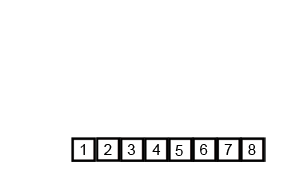
图片来自这里
代码如下:
private void mergeSort(int[] nums, int left, int right) { // 需要左右边界确定排序范围
if (left >= right) return;
int mid = (left+right) / 2;
mergeSort(nums, left, mid); // 先对左右子数组进行排序
mergeSort(nums, mid+1, right);
int[] temp = new int[right-left+1]; // 临时数组存放合并结果
int i=left,j=mid+1;
int cur = 0;
while (i<=mid&&j<=right) { // 开始合并数组
if (nums[i]<=nums[j]) temp[cur] = nums[i++];
else temp[cur] = nums[j++];
cur++;
}
while (i<=mid) temp[cur++] = nums[i++];
while (j<=right) temp[cur++] = nums[j++];
for (int k = 0; k < temp.length; k++) { // 合并数组完成,拷贝到原来的数组中
nums[left+k] = temp[k];
}
}
时间复杂度上归并排序能够稳定在的水平,在每一级的合并排序数组过程中总的操作次数是,总的层级数是,相乘得到最后的结果就是
空间复杂度是,因为在合并的过程中需要使用临时数组来存放临时排序结果。
归并排序是稳定排序,保证原来相同的元素能够保持相对的位置。
快速排序
快速排序(有时称为分区交换排序)是一种高效的排序算法。由英国计算机科学家Tony Hoare于1959年开发并于1961年发表,它在现在仍然是一种常用的排序算法。如果实现方法恰当,它可以比主要竞争对手(归并排序和堆排序)快两到三倍。
其核心的思路是取第一个元素(或者最后一个元素)作为分界点,把整个数组分成左右两侧,左边的元素小于或者等于分界点元素,而右边的元素大于分界点元素,然后把分界点移到中间位置,对左右子数组分别进行递归,最后就能得到一个排序完成的数组。当子数组只有一个或者没有元素的时候就结束这个递归过程。
其中最重要的是将整个数组根据分界点元素划分成左右两侧的逻辑,目前有两种算法,图片展示的是第一种。
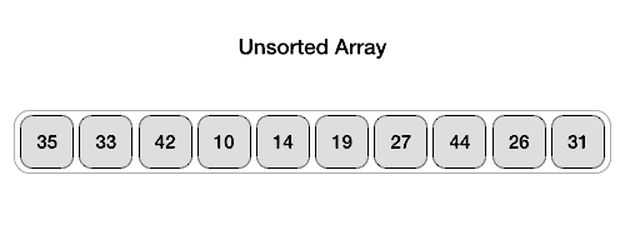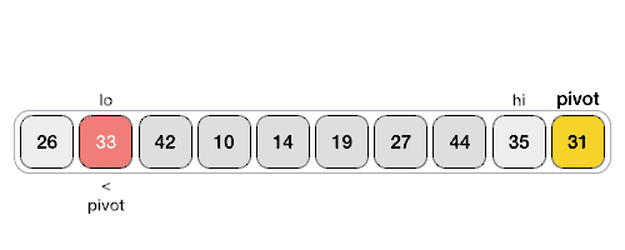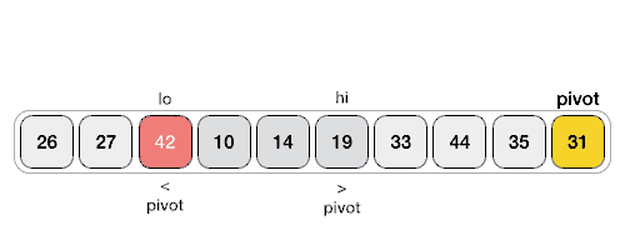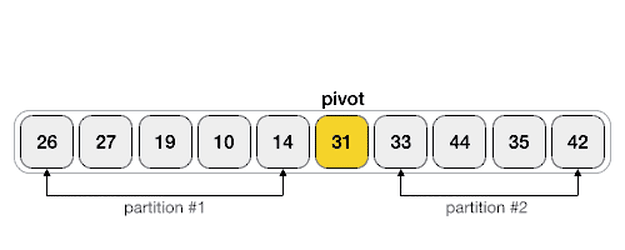
图片来自这里
第一种实现,也是图片中的排序逻辑的实现:
private void quickSort(int[] nums, int left, int right) {
if (left >= right) return;
int lo = left+1; // 小于分界点元素的最右侧的指针
int hi = right; // 大于分界点元素的最左侧的指针
while (lo<=hi) {
if (nums[lo]>nums[left]) { // 交换元素确保左侧指针指向元素小于分界点元素
swap(nums, lo, hi);
hi--;
} else {
lo++;
}
}
lo--; // 回到小于分界点元素数组的最右侧
swap(nums, left, lo); // 将分界点元素移到左侧数组最右侧
quickSort2(nums, left, lo-1);
quickSort2(nums, lo+1, right);
}
第二种,不用hi来标记大于分界点元素的最右侧,而是只用一个lo来标记最左侧。在遍历整个数组的过程中,如果发现了一个小于等于分界点元素的元素,就和lo+1位置的元素交换,然后lo自增,这样可以保证lo的左侧一定都是小于等于分界点元素的,遍历到最后lo的位置就是新的分界点位置,和最开始的分界点元素位置互换。
private void quickSort(int[] nums, int left, int right) {
if (left>=right) return;
int cur = left + 1; // 从左侧第二个元素开始
int lo = left; // 分界点为第一个元素
while (cur <= right) {
if (nums[cur] <= nums[left]) { // 交换位置保证lo的左侧都是小于num[left]
swap(nums, lo+1, cur);
lo ++;
}
cur++;
}
swap(nums, left, lo); // 把分界点元素移动到新的分界位置
quickSort(nums, left, lo-1);
quickSort(nums, lo+1, right);
}
时间复杂度在最佳情况是,但是如果分界点元素选择不当可能会恶化到,但是这种情况比较少见(比如数组完全逆序),如果随机选择分界点的话,时间复杂度能够稳定在。另外如果元素中相同元素数量比较多的话,也会降低排序性能。
空间复杂度在水平,属于堆栈调用,在最坏的情况下空间复杂度还是,平均情况下复杂度是
快速排序是不稳定的,因为包含跳跃式交换元素位置。
堆排序
堆排序是一个效率要高得多的选择排序,首先把整个数组变成一个最大堆,然后每次从堆顶取出最大的元素,这样依次取出的最大元素就形成了一个排序的数组。堆排序的核心分成两个部分,第一个是新建一个堆,第二个是弹出堆顶元素后重建堆。
新建堆不需要额外的空间,而是使用原来的数组,一个数组在另一个维度上可以当作一个完全二叉树(除了最后一层之外其他的每一层都被完全填充,并且所有的节点都向左对齐),对于下标为i的元素,他的子节点是2*i+1和2*i+2(前提是没有超出边界)。在新建堆的时候从左向右开始遍历,当遍历到一个元素的时候,重新排列从这个元素节点到根节点的所有元素,保证满足最大堆的要求(父节点比子节点要大)。遍历完整个数组的时候,这个最大堆就完成了。
在弹出根节点之后(把根节点的元素和树的最底层最右侧的元素互换),堆被破坏,需要重建。从根节点开始和两个子节点比较,如果父节点比最大的子节点小,那么就互换父节点和最大的子节点,然后把互换后在子节点位置的父节点当作新的父节点,和它的子节点比较,如此往复直到最后一层,这样最大堆就重建完毕了。

图片来自这里
简单java代码:
private void heapSort(int[] nums) {
heapify(nums); // 新建一个最大堆
for (int i = nums.length - 1; i >= 1; i--) {
swap(nums, 0, i); // 弹出最大堆的堆顶放在最后
rebuildHeap(nums, 0,i-1); // 重建最大堆
}
}
private void heapify(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int par = (i-1)>>1; // 找到父节点
int child = i; // 定义子节点
while (child>0&&nums[par]<nums[child]) { // 从子节点到根节点构建最大堆
swap(nums, par, child);
child = par;
par = (par-1) >> 1;
}
}
}
private void rebuildHeap(int[] nums, int par, int last) {
int left = 2*par+1; // 左子节点
int right = 2*par+2; // 右子节点
int maxIndex = left;
if (right<=last && nums[right]>nums[left]) { // 找到最大子节点
maxIndex = right;
}
if (left<=last && nums[par] < nums[maxIndex]) {// 和最大子节点比较
swap(nums, par, maxIndex); // 互换到最大子节点
rebuildHeap(nums, maxIndex, last); // 重建最大子节点代表的子树
}
}
时间复杂度稳定在,因为在构建堆的时候时间遍历数组对于每个元素需要进行次比较,时间复杂度是。在弹出每个元素重建堆需要的复杂度,时间复杂度也是,所以整体的时间复杂度是
空间复杂度是,在原数组进行所有操作就可以了。
堆排序是不稳定,堆得构建和重建的过程都会打乱元素的相对位置。
堆排序的代码量相对于其他的排序算法来说是比较多的,理解上也比较难,涉及到最大堆和二叉树等相关概念。虽然在实际使用中相对于快速排序不是那么好用,但是最坏情况下的的时间复杂度也是优于快排的。空间使用是恒定的,是优于归并排序。
二叉搜索树排序
二叉树搜索排序用数组内的所有元素构建一个搜索二叉树,然后用中序遍历重新将所有的元素填充回原来的数组中。因为搜索二叉树不能用数组来表示,所以必须使用额外的数据结构来构建二叉树。

图片来自这里
简单代码如下:
private int[] bstSort(int[] nums) {
TreeNode root = new TreeNode(nums[0]); // 构建根节点
for (int i = 1; i < nums.length; i++) { // 将所有的元素插入到二叉搜索树中
buildTree(root, nums[i]);
}
inorderTraversal(root, nums, new int[1]);// 中序遍历获取二叉树中的所有节点
return nums;
}
private void inorderTraversal(TreeNode node, int[] nums, int[] pos) {
if (node == null) return;
inorderTraversal(node.left, nums, pos);
nums[pos[0]++] = node.val;
inorderTraversal(node.right, nums, pos);
}
private void buildTree(TreeNode node, int num) {
if (node == null) return;
if (num >= node.val) { // 插入到右子树中
if (node.right == null) {
node.right = new TreeNode(num);
} else {
buildTree(node.right, num);
}
} else { // 插入到左子树中
if (node.left == null) {
node.left = new TreeNode(num);
} else {
buildTree(node.left, num);
}
}
}
static class TreeNode { // 树节点的数据结构
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
时间复杂度上面根据原数组变化比较大,最差情况是整个数组是已经排好序的,这样二叉树会变成一个链表结构,时间复杂度退化到了,但是最优和平均情况下时间复杂度在水平。
空间复杂度是,因为要构建一个包含n个元素的二叉搜索树。
这个算法是稳定,在构建二叉树的过程中能够保证元素顺序的一致性。
计数排序
计数排序是一个最基本的非比较排序,能够将时间复杂度提高到的水平,但是使用上比较有局限性,通常只能应用在键的变化范围比较小的情况下,如果键的变化范围特别大,建议使用基数排序。
计数排序的过程是创建一个长度为数组中最小和最大元素之差的数组,分别对应数组中的每个元素,然后用这个新的数组来统计每个元素出现的频率,然后遍历新的数组,根据每个元素出现的频率把元素放回到老的数组中,得到已经排好序的数组。

图片来自这里
简单代码实现:
private void countSort(int[] nums) {
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int num : nums) { // 找到最大最小值
min = Math.min(min, num);
max = Math.max(max, num);
}
int[] count = new int[max-min+1]; // 建立新数组
for (int num : nums) { // 统计每个元素出现频率
count[num-min]++;
}
int cur = 0;
for (int i = 0; i < count.length; i++) { // 根据出现频率把计数数组中的元素放回到旧数组中
while (count[i]>0) {
nums[cur++] = i+min;
count[i]--;
}
}
}
计数排序能够将时间复杂度降低到(r为数组元素变化范围),不过这是对于数组元素的变化范围不是特别大。随着范围的变大,计数排序的性能就会逐渐降低。
空间复杂度为,随着数组元素变化范围的增大,空间复杂度也会变大。
计数排序是稳定的,原来排在前面的相同在计数的时候,仍然是排在每个计数位置的前面,在最后复原的时候也是从每个计数位的前面开始复原,所以最后相对位置还是相同的。
桶排序
桶排序是将所有的元素分布到一系列的区间(也可以称之为桶)里面,然后对每个桶里面的所有元素分别进行排序的算法。
首先新建一个桶的数组,每个桶的规则需要提前制定好,比如元素在09为一个桶、1019为一个桶。然后遍历整个待排序的数组,把元素分配到对应的桶里面。接下来单独对每个桶里面的元素进行排序,排序算法可以选择比较排序或者非比较排序,得到排序后的数组。最后把所有的桶内的元素还原到原数组里面得到最后的排序数组。
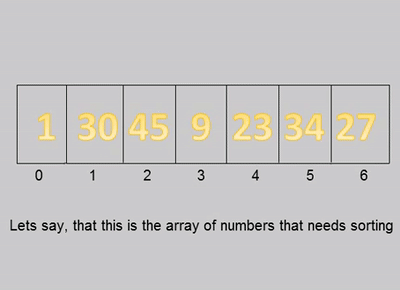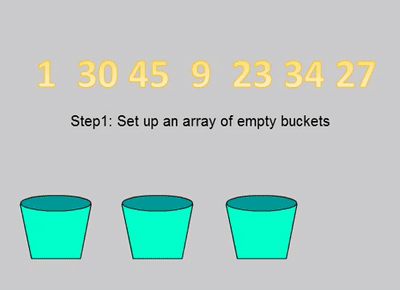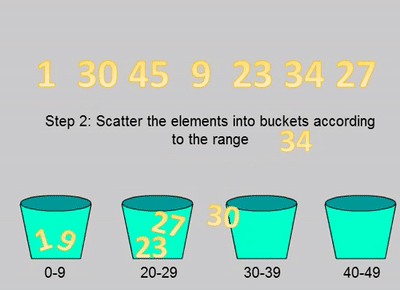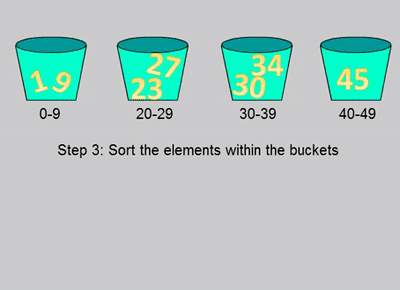
图片来自这里
private void bucketSort(int[] nums) {
int INTERVAL = 100; // 定义桶的大小
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int num : nums) { // 找到数组元素的范围
min = Math.min(min, num);
max = Math.max(max, num);
}
int count = (max - min + 1); // 计算出桶的数量
int bucketSize = (count % INTERVAL == 0) ?( count / INTERVAL) : (count / INTERVAL+1);
List<Integer>[] buckets = new List[bucketSize];
for (int num : nums) { // 把所有元素放入对应的桶里面
int quotient = (num-min) / INTERVAL;
if (buckets[quotient] == null) buckets[quotient] = new ArrayList<>();
buckets[quotient].add(num);
}
int cur = 0;
for (List<Integer> bucket : buckets) {
if (bucket != null) {
bucket.sort(null); // 对每个桶进行排序
for (Integer integer : bucket) { // 还原桶里面的元素到原数组
nums[cur++] = integer;
}
}
}
}
时间复杂度上桶排序和计数排序一样,是的水平,但是随着数据元素范围的增大,时间消耗也在增大。
空间复杂度也是,需要额外的空间来保存所有的桶和桶里面的元素。
桶排序是稳定的(前提是桶内排序的逻辑是稳定的),和计数排序的逻辑类似,遍历过程插入桶的过程中没有改变相同元素的相对位置,排序也没有改变,最后的还原也没有改变。
基数排序
基数排序和桶排序有点相似,基数排序中需要把元素送入对应的桶中,不过规则是根据所有数字的某一位上面的数字来分类。
假设当前数组的所有元素都是正数,桶的数量就固定在了10个,然后计算出最大元素的位数。首先根据每个元素的最低位进行分组,比如1就放入1这个桶,13就放入3这个桶,111也放入1这个桶,然后把所有的数字根据桶的顺序取出来,依次还原到原数组里面。在第二轮从第二位开始分组,比如1(看作01)放入0这个桶,13放入1这个桶,111也放入1这个桶,再把所有的元素从桶里面依次取出放入原数组。经过最大元素位数次的这样的操作之后,还原得到的数组就是一个已经排好序的数组。

图片来自这里
考虑到数组里面还有负数的情况,可以把桶的大小扩大到19个,分别代表对应位在-9~9之间的数字,代码如下:
private void radixSort(int[] nums) {
int max = -1;
int min = 1;
for (int num : nums) { // 计算最大最小值
max = Math.max(max, num);
min = Math.min(min, num);
}
max = Math.max(max, -min); // 求得绝对值最大的值
int digits = 0;
while (max > 0) { // 计算绝对值最大的值的位数
max /= 10;
digits++;
}
List<Integer>[] buckets = new List[19]; // 建一个包含所有位数的数组
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new ArrayList<>();
}
int pos;
int cur;
for (int i = 0, mod = 1; i < digits; i++, mod*=10) { // 对十进制每一位进行基数排序
for (int num : nums) { // 扫描数组将值放入对应的桶
pos = (num / mod) % 10;
buckets[pos+9].add(num);
}
cur = 0;
for (List<Integer> bucket : buckets) { // 将桶内元素放回到数组里面
if (bucket!=null) {
for (Integer integer : bucket) {
nums[cur++] = integer;
}
bucket.clear(); // 将桶清空
}
}
}
}
时间复杂度基本在水平,其中为key的总数量,为绝对值最大的数字的十进制位数。
空间复杂度是。
基数排序是一个稳定排序算法,在排序添加元素的过程中没有改变相同元素的相互位置。
TimSort
Timsort是由Tim Peters在2002年实现的,自Python 2.3以来,它一直是Python的标准排序算法。Java在JDK中使用Timsort对非基本类型进行排序。Android平台和GNU Octave还将其用作默认排序算法。
Timsort是一种稳定的混合排序算法,同时应用了二分插入排序和归并排序的思想,在时间上击败了其他所有排序算法。它在最坏情况下的时间复杂度为优于快速排序;最佳情况的时间复杂度为,优于归并排序和堆排序。
由于使用了归并排序,使用额外的空间保存数据,TimSort空间复杂度是
由于篇幅原因,TimSort的具体实现过程暂且就不讲了,感兴趣的同学可以看我的另外一篇博客——世界上最快的排序算法——Timsort
总结
| 排序算法 | 最好情况 | 平均情况 | 最差情况 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | ✓ | ||||
| 选择排序 | |||||
| 插入排序 | ✓ | ||||
| 希尔排序 | |||||
| 二叉树排序 | ✓ | ||||
| 归并排序 | ✓ | ||||
| 快速排序 | |||||
| 堆排序 | |||||
| 计数排序 | - | ✓ | |||
| 桶排序 | - | ✓ | |||
| 基数排序 | - | ✓ | |||
| TimSort | ✓ |
备注:为排序数字的范围,是数字总位数,是数字总个数
上面的表格总结了讲到的排序算法的时间和空间复杂度以及稳定性等,在实际应用中会有各种排序算法变形的问题,都可以通过优化排序算法来达到优化算法的目的。
如果对时间复杂度要求比较高并且键的分布范围比较广,可以使用归并排序、快速排序和堆排序。
如果不能使用额外的空间,那么快速排序和堆排序都是不错的选择。
如果规定了排序的键的范围,可以优先考虑使用桶排序。
如果不想写太多的代码同时时间复杂度没有太高的要求,可以考虑冒泡排序、选择排序和插入排序。
如果排序的过程中没有复杂的额外操作,直接使用编程语言内置的排序算法就行了。
参考
超详细十大经典排序算法总结(java代码)
十大经典排序算法
十大经典排序算法(动图演示)
Sorting algorithm
Timsort
Data Structure - Sorting Techniques
This is the fastest sorting algorithm ever
TimSort
Timsort: The Fastest sorting algorithm for real-world problems
更多内容请看我的个人博客




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义