Decision tree and the ID3 algorithm

In data mining there are four main problems, clustering, classifying, regression and dimension reduce, to be discussed. And this issue is mainly about Decision Tree in classification. For some data that we’ve known, calculate the decision tree, and use the tree to deal with new points, telling which group the new, coming points belong to.

         For one decision tree, each node is one decision and its leaves are the final decisions. Taking the following graph as an example:

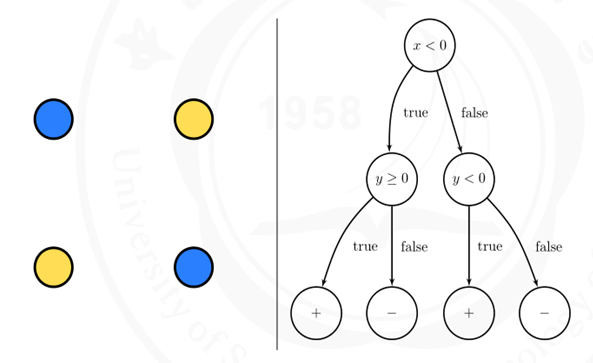
Figure1

To solve the problem that split the dataset randomly making the decision tree too high, Figure2 e.g., we use the ID3 algorithm to split the dataset into subsets having an information entropy as small as possible.

Figure2

Among all the possible splits, ID3 pick the one that maximize the entropy gain.

Examples:

1. 8bits strings:

dataset1 {11110000, 10101010, 11000011}

dataset2 {00000000, 11111111}

For every element in dataset1 the entropy is:

                            E(S1) =-(4/8)*log(4/8)-(1-4/8)*log(1-4/8)= 1

For every element in dataset2 the entropy is:

                            E(S2) =-(8/8)*log(8/8)= 0

　　2.　8 points, 2 of them are red and 6 of them are blue. Split the dataset by line x=2

                            When classify the data above, the decision tree can be like this:

 

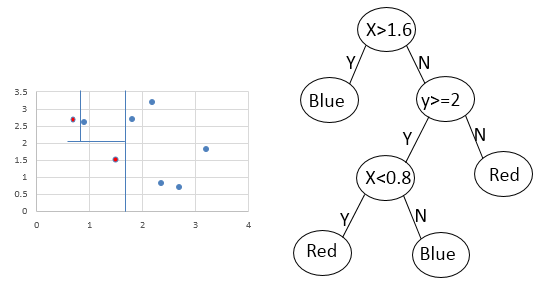
References:

http://www.marmakoide.org/download/teaching/dm/dm-decision-trees.pdf

More information about decision tree demo using ID3 algorithm.