算法设计：寻找多数元素

 

 

在上节的算法设计课堂上，我们学习了寻找多数元素的算法，这个算法相对于我们以前学习的算法比较不好理解，今天就让我们来看看这个算法

1.思路解析

1.1多数元素定义

多数元素表示在一个数组中出现次数最多，并且出现次数 > 数组总长度的一半的元素。例如数组a = {1,7,5,5,5,5,5,4}，数组总长度为8，5在其中出现了5次，大于8/2=4次，因此5是多数元素。

而在数组b = {1,2,5,5,5,9,7,6,4}，数组总长度为9，5虽然同样是出现次数最多的元素，但他的出现次数只有3次，因而不能算作多数元素。、

1.2遍历计数法

遍历计数法可谓是最简单粗暴的方法，其思路是对数组中出现的每一个元素，都遍历一遍求出其出现次数，再从中找出多数元素，这种算法的优点在于容易想到，但这种算法的计算量实在太大，因此不推荐

1.3排序取中项法

排序取中项法相对于前一个方法来说进步了一些，其使用的原理是：

• 在一个排好序的数组中，其最中间的元素必定是多数元素（如果有的话）

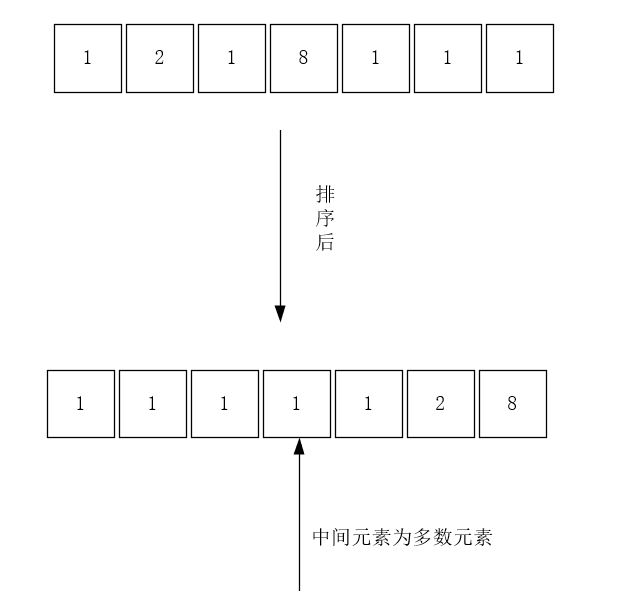
但这种算法也有其劣势，就是它要求数组进行排序，在数组长度较大的时候，其计算代价也是较大的

1.4剔除元素法（推荐方法）

因此我们使用推荐的算法，这个算法基于的原理是：

• 在原序列中去除两个不同的元素后，原序列中的多数元素在新序列中还是多数元素。

那么问题就简单了，我们只需要将数组中不相同的元素两两剔除，那么剩下的数就自然是多数元素。

我们可以将数组的第一个元素设置为多数元素候选c，以及计数器count = 1，将数组后面的数与c比较，若相等count+1，不相等count-1，若count减到0，便表示该元素出现次数太少，将其和后面一个不相等的元素剔除，再次重置c和count，继续此操作，直到比较到最后count都不为0，则c就为多数元素。

这种算法将复杂过程简化成了两数的比较，大大提升了计算效率。

2.算法伪码

该算法的伪码如下：

MAJORITY(n):

1. c←candidate(1)
2. count←0
3. for j←1 to n
4.     if a[j] = c then count←count+1
5. end for
6. if count > n/2(取下线) then return c
7. else return none

candidate(m):

1. j←m; c←a[m]; count←1
2. while j<n and count>0
3.     j←j+1
4.     if a[j] = c then count←count+1
5.     else count←count-1
6. end while
7. if j=n then return c
8. else return candidate(j+1)

3.具体代码

算法部分如下：

//寻找多数元素算法练习
public class Marjority {
    private int a[] = new int[50];    //定义存放数据的数组
    public int length;        //定义数组长度
    public Marjority(int length,int a[])
    {
        for(int i=1;i<=length;i++)
            this.a[i] = a[i-1];    //转存数组
            /*需要注意的是，我们的算法中数组下标从1开始
             * 但java存储时的数组下标从0开始，所以转存时下标需-1*/
        this.length = length;
    }
    //寻找多数元素，若存在则输出，不存在返回-99999
    public int Mar()
    {
        int c = candidate(1);
        //进行多数元素查询
        int count = 0;
        for(int j=1;j<=length;j++)
            if(a[j] == c)
                count++;    //计算该元素在数组中出现的次数
        if(count > length/2)    //判断出现次数是否大于长度的一半
            return c;    //大于则有多数元素，返回其值
        else return -9999;    //不大于则没有多数元素，返回-9999
    }
    public int candidate(int n)
    {
        int j = n, c = a[n], count = 1;
        //声明数组索引，当前元素值，计数器
        while(j<length && count>0)
        {
            j++;    //指针向后移动一位
            if(a[j] == c)    //若下一位与当前元素相同，计数器增加
                count++;
            else count--;    //否则计数器减少
            /*这里不太好理解的是计数器的作用，
             * 实际上计数器是一个筛选作用，
             * 当当前元素重复出现的次数太少时，
             * 将这个元素剔除出候选*/
        }
        if(j == length)
            return c;    /*当指针指向最后一个元素时，
                           表示当前元素出现次数足够多，
                           返回其值*/
        else return candidate(j+1);    //否则继续向后遍历
    }
}

 测试部分如下：

public class TestMarjority {
    public static void main(String args[])
    {
        int a[] = {1, 2, 5, 5, 5, 5, 5, 1, 3};    //含有多数元素的数组
        int b[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};    //不含有多数元素的数组
        Marjority m1 = new Marjority(a.length, a);
        Marjority m2 = new Marjority(b.length, b);
        System.out.println(m1.Mar());
        System.out.println(m2.Mar());
    }
}

 输出结果如下：