算法设计:两种快速排序代码实现
快速排序是一种高效且使用广泛的排序算法,在很多语言的标准库中自带的排序都是快速排序,所以我们也有必要了解快排的原理以及其实现方法。
快排的大致思想
快速排序实现的重点在于数组的拆分,通常我们将数组的第一个元素定义为比较元素,然后将数组中小于比较元素的数放到左边,将大于比较元素的放到右边,
这样我们就将数组拆分成了左右两部分:小于比较元素的数组;大于比较元素的数组。我们再对这两个数组进行同样的拆分,直到拆分到不能再拆分,数组就自然而然地以升序排列了。

不难看出,拆分算法是整个快速排序中的核心,快速排序拥有非常多的拆分方式,在本篇文章中我们介绍其中的两种,我个人将它称作:单指针遍历法与双指针遍历法(在下文中用英文单词split和partition称呼)
split算法解析
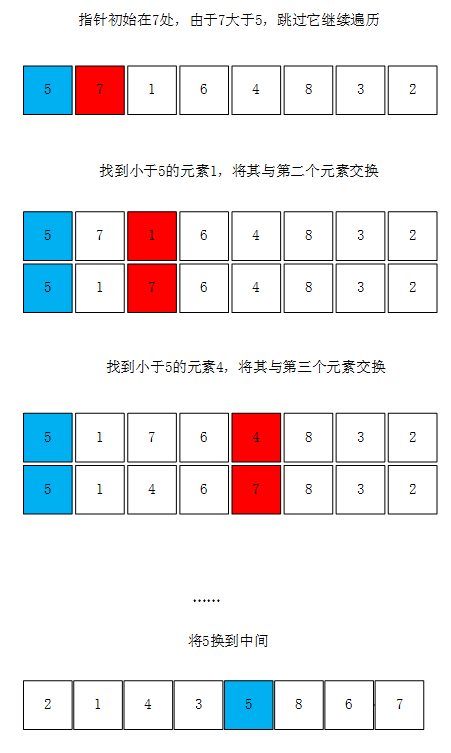
split算法使用一个单向的指针来对数组进行遍历,首先将数组首元素设置为比较元素,然后将第二个开始的元素依次与比较元素比较,如果大于比较元素则跳过,如果小于比较元素,则将其与前面较大的元素进行交换,将数组中所有元素交换完毕后,再将比较元素放到中间位置。
split算法实现(c):
1 //划分数组的函数 2 int split(int a[], int low, int high) 3 { 4 int i = low; //i指向比较元素的期望位置 5 int x = a[i]; //将该数组第一个元素设置为比较元素 6 //从数组的第二个元素起开始遍历,若找到的元素大于比较元素,则跳过 7 for(int j = low+1;j<=high;j++) 8 //若找到了小于比较元素的数,则将其与前面较大的数进行交换 9 if (a[j] <= x) 10 { 11 i++; 12 swap(a[i], a[j]); 13 } 14 swap(a[low], a[i]); //将比较元素交换到期望位置 15 return i; 16 }
split算法实现(java):
1 //划分数组 2 public static int split(int a[], int low, int high) 3 { 4 int i = low; //i指向比较元素的期望位置 5 int x = a[low]; //将该组的第一个元素作为比较元素 6 //从第二个元素开始,若当前元素大于比较元素,将其跳过 7 for(int j = low+1; j <= high; j++) 8 //若找到了小于比较元素的元素,将其与前面较大的元素进行交换 9 if(a[j] <= x) 10 { 11 i++; 12 if(i != j) 13 swap(a, i, j); 14 15 } 16 swap(a, i, low); //将比较元素交换到正确的位置上 17 return i; //返回比较元素的位置 18 }
partition算法解析
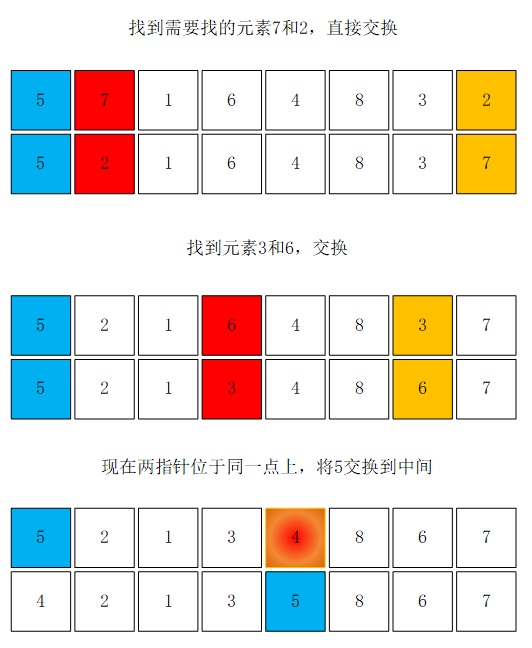
partition算法使用头尾两个方向相反的指针进行遍历,先将数组第一个元素设置为比较元素,头指针从左至右找到第一个大于比较元素的数,尾指针从右至左找到第一个小于比较元素的数,全部交换完毕后将比较元素放到中间位置。
partition算法实现(c):
1 int partition(int a[], int low, int high) 2 { 3 int x = a[low]; //将该数组第一个元素设置为比较元素 4 int i = low; //指向数组头的指针 5 int j = high; //指向数组尾的指针 6 while (i < j) 7 { 8 while (i < j && a[j] >= x) 9 j--; //从右至左找到第一个小于比较元素的数 10 while (i < j && a[i] <= x) 11 i++; //从左至右找到第一个大于比较元素的数 12 /*需要注意的是,这里的j--与i++的顺序不可以调换! 13 如果调换了顺序,i会走过头,以至于将后面较大的元素交换到数组开头*/ 14 15 //将大数与小数交换 16 if (i != j) 17 swap(a[i], a[j]); 18 } 19 swap(a[low], a[i]); //将比较元素交换到期望位置 20 return i; //返回比较元素的位置 21 }
partition算法实现(java):
1 //划分数组 2 public static int partition(int a[], int low, int high) 3 { 4 int x = a[low]; //将该数组第一个元素设置为比较元素 5 int i=low; 6 int j=high; 7 while(i < j) 8 { 9 while(i<j && a[i] <= x) 10 i++; 11 while(i<j && a[j] >= x) 12 j--; 13 14 15 if(i!=j) 16 swap(a, i, j); 17 } 18 swap(a, j, low); 19 return j; 20 }
两种算法的完整代码和实际演示
split算法(c):
1 #include<stdio.h> 2 3 void swap(int &a, int &b) 4 { 5 int t = a; 6 a = b; 7 b = t; 8 } 9 10 //划分数组的函数 11 int split(int a[], int low, int high) 12 { 13 int i = low; //i指向比较元素的期望位置 14 int x = a[i]; //将该数组第一个元素设置为比较元素 15 //从数组的第二个元素起开始遍历,若找到的元素大于比较元素,则跳过 16 for(int j = low+1;j<=high;j++) 17 //若找到了小于比较元素的数,则将其与前面较大的数进行交换 18 if (a[j] <= x) 19 { 20 i++; 21 swap(a[i], a[j]); 22 } 23 swap(a[low], a[i]); //将比较元素交换到期望位置 24 return i; 25 } 26 27 //快速排序 28 void quicksort(int a[], int low, int high) 29 { 30 if (low < high) 31 { 32 int i = split(a, low, high); //划分数组并获得比较元素位置 33 quicksort(a, low, i - 1); //对比较元素左边进行排序 34 quicksort(a, i + 1, high); //对比较元素右边进行排序 35 } 36 } 37 38 int main() 39 { 40 int a[] = { 5,7,1,6,4,8,3,2 }; 41 int length = sizeof(a) / sizeof(a[0]); 42 quicksort(a, 0, length - 1); 43 for (int i = 0; i < length; i++) 44 printf("%d ", a[i]); 45 printf("\n"); 46 return 0; 47 }
split算法(java):
1 //快速排序split实现方法 2 public class T1 { 3 public static void main(String args[]) 4 { 5 int a[] = {5,7,1,6,4,8,3,2}; 6 quickSort(a, 0, a.length-1); 7 for(int i=0;i<a.length;i++) 8 System.out.print(a[i] + " "); 9 System.out.println(); 10 } 11 12 //交换方法 13 public static void swap(int a[], int i, int j) 14 { 15 int t = a[i]; 16 a[i] = a[j]; 17 a[j] = t; 18 } 19 20 //划分数组 21 public static int split(int a[], int low, int high) 22 { 23 int i = low; //i指向比较元素的期望位置 24 int x = a[low]; //将该组的第一个元素作为比较元素 25 //从第二个元素开始,若当前元素大于比较元素,将其跳过 26 for(int j = low+1; j <= high; j++) 27 //若找到了小于比较元素的元素,将其与前面较大的元素进行交换 28 if(a[j] <= x) 29 { 30 i++; 31 if(i != j) 32 swap(a, i, j); 33 34 } 35 swap(a, i, low); //将比较元素交换到正确的位置上 36 return i; //返回比较元素的位置 37 } 38 39 public static void quickSort(int a[], int low, int high) 40 { 41 if(low < high) 42 { 43 int i = split(a, low, high); //划分并获取比较元素的位置 44 quickSort(a, low, i-1); //对比较元素左边的数组进行排序 45 quickSort(a, i+1, high); //对比较元素右边的数字进行排序 46 } 47 } 48 }

partition算法(c):
1 #include<stdio.h> 2 3 //交换函数 4 void swap(int &a, int &b) 5 { 6 int t = a; 7 a = b; 8 b = t; 9 } 10 11 int partition(int a[], int low, int high) 12 { 13 int x = a[low]; //将该数组第一个元素设置为比较元素 14 int i = low; //指向数组头的指针 15 int j = high; //指向数组尾的指针 16 while (i < j) 17 { 18 while (i < j && a[j] >= x) 19 j--; //从右至左找到第一个小于比较元素的数 20 while (i < j && a[i] <= x) 21 i++; //从左至右找到第一个大于比较元素的数 22 /*需要注意的是,这里的j--与i++的顺序不可以调换! 23 如果调换了顺序,i会走过头,以至于将后面较大的元素交换到数组开头*/ 24 25 //将大数与小数交换 26 if (i != j) 27 swap(a[i], a[j]); 28 } 29 swap(a[low], a[i]); //将比较元素交换到期望位置 30 return i; //返回比较元素的位置 31 } 32 33 void quicksort(int a[], int low, int high) 34 { 35 if (low < high) 36 { 37 int i = partition(a, low, high); //划分数组并获取比较元素的位置 38 quicksort(a, low, i - 1); //对比较元素左边进行排序 39 quicksort(a, i + 1, high); //对比较元素右边进行排序 40 } 41 } 42 43 int main() 44 { 45 int a[] = { 5,7,1,6,4,8,3,2 }; 46 int length = sizeof(a) / sizeof(a[0]); 47 quicksort(a, 0, length - 1); 48 for (int i = 0; i < length; i++) 49 printf("%d ", a[i]); 50 printf("\n"); 51 return 0; 52 }

partition算法(java):
1 //快速排序partition实现方法 2 public class T2 { 3 public static void main(String args[]) 4 { 5 int a[] = {5,7,1,6,4,8,3,2}; 6 quicksort(a, 0, a.length-1); 7 for(int i=0;i<a.length;i++) 8 System.out.print(a[i] + " "); 9 System.out.println(); 10 } 11 12 public static void swap(int a[], int i, int j) 13 { 14 int t = a[i]; 15 a[i] = a[j]; 16 a[j] = t; 17 } 18 19 //划分数组 20 public static int partition(int a[], int low, int high) 21 { 22 int x = a[low]; //将该数组第一个元素设置为比较元素 23 int i=low; 24 int j=high; 25 while(i < j) 26 { 27 while(i<j && a[j] >= x) 28 j--; //从右至左找到第一个小于比较元素的数 29 while(i<j && a[i] <= x) 30 i++; //从左至右找到第一个大于比较元素的数 31 /*需要注意的是,这里的j--与i++的顺序不可以调换! 32 *如果调换了顺序,i会走过头,以至于将后面较大的元素交换到数组开头*/ 33 34 //将大数与小数交换 35 if(i!=j) 36 swap(a, i, j); 37 } 38 swap(a, i, low); //将比较元素交换到期望位置 39 return i; //返回比较元素的位置 40 } 41 42 public static void quicksort(int a[], int low, int high) 43 { 44 if(low < high) 45 { 46 int i = partition(a, low, high); //划分数组并获取比较元素的位置 47 quicksort(a, low, i-1); //对比较元素左边进行排序 48 quicksort(a, i+1, high); //对比较元素右边进行排序 49 } 50 } 51 }