决策树(ID3)
1信息增益
划分数据的最大原则就是:将无序的数据变得更加有序。
在划分数据集之前之后信息发生的变化称为信息增益,通过计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。
度量集合信息的方式简称为熵。另一个度量集合无序程度的方法是基尼不纯度。
计算信息熵的代码实现
from math import log
def calShannonEnt(dataSet):
'''
计算给定数据集的熵
:param dataSet:
:return:
'''
numEntries = len(dataSet)
labelCounts = {}
# 为所有可能分类创建字典
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries # 使用标签出现的频率计算类别出现的概率
shannonEnt -= prob * log(prob, 2) # 以2为底求对数
return shannonEnt
PS:熵定义为信息的期望值,
如果待分类的事务可能划分在多个分类之中,则符合xi的信息的定义为:
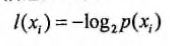 其中p(xi)是选择该分类的概率。
其中p(xi)是选择该分类的概率。
为了计算熵,我们需要计算所有类别所有可能值包含的信息期望,通过下面的公式得到:
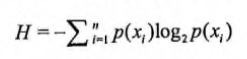 其中n是分类的数目。
其中n是分类的数目。
创建数据集
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels
2划分数据集
按照给定特征划分数据集
def splitDataSet(dataSet, axis, value):
'''
:param dataSet:待划分的数据集
:param axis: 划分数据集的特征
:param value: 特征的返回值
:return:
'''
retDateSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis + 1:]) # extend 合并列表方法 例:[1,2,3].extend([5,6,7]) => [1,2,3,4,5,6]
retDateSet.append(reducedFeatVec)
return retDateSet
选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
'''
实现选取特征,划分数据集
:param dataSet:
:return: 最佳特征的index,用于划分数据集的特征
'''
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet) # 整个数据集的原始熵
bestInfoGain, bestFeature = 0.0, -1
for i in range(numFeatures):
# 创建唯一的分类标签列表
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
# 计算每种划分方式的信息熵
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if infoGain > bestInfoGain:
# 计算最好的信息增益
bestInfoGain = infoGain
bestFeature = i
return bestFeature
3递归构建决策树
多数表决方法决定叶子节点的分类
def majorityCnt(classList):
'''
:param classList: 分类名称列表
:return:出现次数最多的分类名称
'''
classCount = {}
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
创建树的函数代码
def createTree(dataSet, labels):
'''
:param dataSet:数据集
:param labels: 标签列表(数据集中所有特征的标签)
:return:
'''
classList = [example[-1] for example in dataSet] # 数据集中所有类标签
# 类别完全相同则停止继续划分
if classList.count(classList[0]) == len(classList):
return classList[0]
# 遍历完所有特征时返回出现次数最多的
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) # 最好特征
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel: {}}
# 得到列表包含的所有属性值
del labels[bestFeat]
featVlaues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featVlaues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) # 递归调用createTree
return myTree
if __name__ == '__main__':
myData, labels = createDataSet()
res = createTree(myData, labels)
print(res)
'''
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
'''
4使用决策树执行分类
def classify(inputTree, featLabels, testVec):
'''
使用决策树的分类函数
:param inputTree:
:param featLabels:
:param testVec:
:return:
'''
firstStr = list(inputTree.keys())[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr) # 将标签字符串转换为索引
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
else:
classLabel = secondDict[key]
return classLabel
if __name__ == '__main__':
myData, labels = trees.createDataSet()
print(labels)
myTree = trees.createTree(myData, labels.copy()) # 浅拷贝,否则labels会被修改
print(myTree)
print(trees.classify(myTree, labels, [1, 0]))
print(trees.classify(myTree, labels, [1, 1]))
5决策树的存储,如何在硬盘上存储决策树分类器
# 使用pickles模块存储决策树
def storeTree(inputTree, filename):
import pickle
fw = open(filename, 'wb')
pickle.dump(inputTree, fw)
fw.close()
def grabTree(filename):
import pickle
fr = open(filename, 'rb')
return pickle.load(fr)
if __name__ == '__main__':
myData, labels = trees.createDataSet()
myTree = trees.createTree(myData, labels.copy())
trees.storeTree(myTree, 'classifierStorage.txt')
res = trees.grabTree('classifierStorage.txt')
print(res)





