k-临近算法
工作原理:
1.假设一个带有标签的样本数据集(训练样本集),其中每条数据与其分类有对应关系。
2.输入没有标签的新数据后,将新数据中的每个特征与样本数据集中的每个特征进行比较。
2.1 计算新数据与样本数据集中的每条数据的距离。
2.2 对求得的每个距离进行排序(从小到大排序)
2.3 取前k个样本数据的分类标签。
3.取前k个数据中出现次数最多的分类标签作为新数据的分类。
通俗理解:
给定训练样本集,对于新输入实例,在训练样本集中找到与该实例最接近的k个实例,这k个实例中多数属与某个类,就把该输入实例分为这个类。
代码实现:
# !/usr/bin/env python3
# -*- coding: utf-8 -*-
from numpy import *
import operator # 运算符
def createDataSet():
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
labels = ['A', 'A', 'B', 'B']
return group, labels
def classify0(inX, dataSet, labels, k):
'''
k-临近算法
:param inX: 用于分类的输入向量
:param dataSet: 输入的训练样本集
:param labels: 标签向量
:param k: 用于选择最近邻居的数目
:return: 发生频率最高的元素标签
'''
dataSetSize = dataSet.shape[0] # dataSet行数
# 使用欧氏距离公式,计算两个向量点之间的距离 -- start
diffMat = tile(inX, (dataSetSize, 1)) - dataSet # 将inX纵向复制 后减dataSet
sqDiffMat = diffMat ** 2 #
sqDistances = sqDiffMat.sum(axis=1) # 每一行相加
distances = sqDistances ** 0.5 # 开根号 [ 1.48660687 1.41421356 0. 0.1 ]
# -- end
sortedDistIndicies = distances.argsort() # 将数组按照从小到大的顺序排序,并按照对应的索引值输出 [2 3 1 0]
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 # get返回指定键的值,如果值不在字典中返回默认值
# sorted 可以对所有可迭代的对象进行排序操作 ;operator.itemgetter(1) 指定取待排对象的第1个域进行排序
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
if __name__ == '__main__':
group, labels = createDataSet()
classify0([0, 0], group, labels, 3)
PS:欧氏距离公式,计算两个向量点xA和xB之间的距离:

例如,点(0,0)与(1,2)之间的距离计算为:
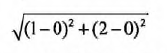


 浙公网安备 33010602011771号
浙公网安备 33010602011771号