混淆矩阵
一:混淆矩阵(引自qq_28448117的博客)
监督学习—混淆矩阵
非监督学习—匹配矩阵
矩阵每一列代表预测值,每一行代表的是实际的类别。这个名字来源于它可以非常容易的表明多个类别是否有混淆(也就是一个class被预测成另一个class)。
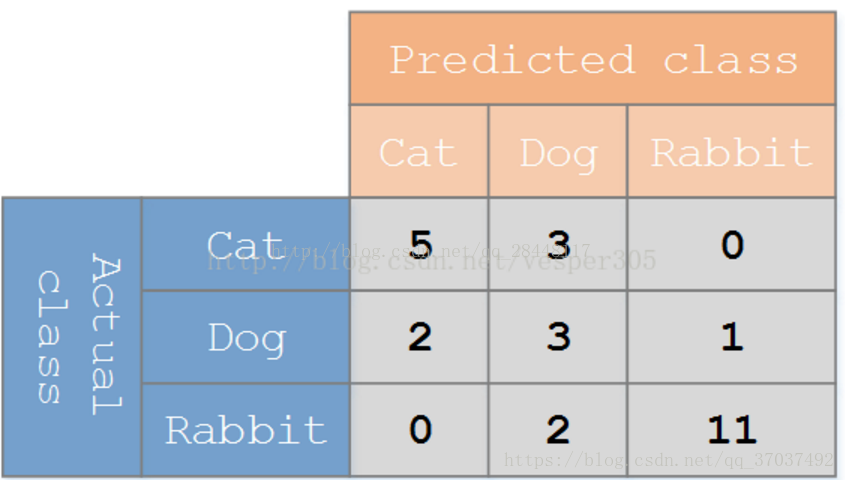
假设有一个用来对猫(cats)、狗(dogs)、兔子(rabbits)进行分类的系统,混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有 27 只动物:8只猫, 6条狗, 13只兔子。结果的混淆矩阵如上图:
在这个混淆矩阵中,实际有8只猫,但是系统将其中3只预测成了狗;对于6条狗,其中有1条被预测成了兔子,2条被预测成了猫。从混淆矩阵中我们可以看出系统对于区分猫和狗存在一些问题,但是区分兔子和其他动物的效果还是不错的。所有正确的预测结果都在对角线上,所以从混淆矩阵中可以很方便直观的看出哪里有错误,因为他们呈现在对角线外面。
二:混淆表格
在预测分析中,混淆表格(有时候也称为混淆矩阵),是由false positives,falsenegatives,true positives和true negatives组成的两行两列的表格。它允许我们做出更多的分析,而不仅仅是局限在正确率,对于上面的矩阵,可以表示为下面的表格
查准率 = 精度 = precision
查全率 = 召回率 = recall
三、对于FN FP TN TP 的解释
precesion:查准率,即在检索后返回的结果中,真正正确的个数占整个结果的比例。
recall:查全率,即在检索结果中真正正确的个数 占整个数据集(检索到的和未检索到的)中真正正确个数的比例。
FN:False Negative,被判定为负样本,但事实上是正样本。
FP:False Positive,被判定为正样本,但事实上是负样本。
TN:True Negative,被判定为负样本,事实上也是负样本。
TP:True Positive,被判定为正样本,事实上也是证样本。
这里的正样本和负样本与检索的关系就是:你认为为正样本的应该都出现在检索结果中,而你认为为负样本的应该不出现在检索结果中,但是你认为的和事实上的会有不一样。
这里的四个缩写曾经一度让我很难记住,经过细想,发现这样比较好记忆:把缩写分为两个部分,第一个字母(F,T)和第二个字母(P,N)。首先搞清楚第二个字母,即它是你认为该样本的归属应该是怎样(Positive or Negative);第一个字母即是对你的判断进行的评价(False or True)。这里也许中文可能会有不好理解的地方,所以我想用英文来描述,可能更清晰:第二个字母:What’s your judgement about the sample?;第一个字母:Is your judgement right(true) or not(false)?
那么有:
precesion = TP/(TP+FP) 即,检索结果中,都是你认为应该为正的样本(第二个字母都是P),但是其中有你判断正确的和判断错误的(第一个字母有T ,F)。
recall = TP/(TP+FN)即,检索结果中,你判断为正的样本也确实为正的,以及那些没在检索结果中被你判断为负但是事实上是正的(FN)。
四、精确率和召回率是不是容易混淆呢?原文链接
实际上非常简单,精确率是针对我们预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了,一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP),也就是而召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN)。其实就是分母不同,一个分母是预测为正的样本数,另一个是原来样本中所有的正样本数。
举个栗子:
假设我们手上有60个正样本,40个负样本,我们要找出所有的正样本,系统查找出50个,其中只有40个是真正的正样本,计算上述各指标。
TP: 将正类预测为正类数 40
FN: 将正类预测为负类数 20
FP: 将负类预测为正类数 10
TN: 将负类预测为负类数 30
准确率(accuracy) = 预测对的/所有 = (TP+TN)/(TP+FN+FP+TN) = 70%
精确率(precision) = TP/(TP+FP) = 80%
召回率(recall) = TP/(TP+FN) = 2/3


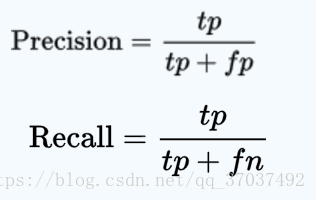

 浙公网安备 33010602011771号
浙公网安备 33010602011771号