Elastic：倒排索引的两种压缩算法：FOR算法和RBM算法

位（bit）、字节(Byte)、MB(兆位)之间的换算关系
在java基本数据类型中，
一个int是4个字节，也就是32个比特位；
一个short类型占用的是2个字节也就是16个字节

B是Byte的缩写，B就是Byte，也就是字节（Byte）；b是bit的缩写，b就是bit，也就是比特位（bit）。
B与b不同，注意区分，KB是千字节，Kb是千比特位。

1MB（兆字节） = 1024KB（千字节）= 1024*1024B(字节) = 1048576B(字节)；
8bit（比特位）= 1Byte（字节）；
1024Byte（字节）= 1KB(千字节)；
1024KB（千字节）= 1MB（兆字节）;
1024MB = 1GB;
1024GB = 1TB;

 

倒排索引解决的问题就是经过分词器分过的单词会保存一个有序数组表示这个单词在哪些文档中出现过，如果单词在很多文档中出现那么这个有序数组怎么存储就成了一个问题。
今天主要介绍两种算法:FOR算法和RBM算法

FOR算法(Frame Of Reference)

 

FOR算法的核心思想是用减法来削减数值大小，从而达到降低空间存储。
假设V(n)表示数组中第n个字段的值，那么经过FOR算法压缩的数值V(n)=V(n)-V(n-1)。也就是说存储的是后一位减去前一位的差值。存储是也不再按照int来计算了，而是看这个数组的最大值需要占用多少bit来计算。
具体我们通过一个例子来体会：
比如数组是73,300,302,332,342,372，每一个int类型数据是4个字节byte，原本需要4 * 6 byte = 24byte =24x8bit比特位= 192bit
压缩后：73,227,2,30,11,29
这些数中227是最大的，需要8bit（227 < 2^8）,
来盛装，那么每个数值都不会超过8bit，所以需要的大小是6 * 8bit=48bit，
我们把8bit的容器理解为一个箱子，总共需要6个箱子，所有箱子占48bit，但是这并不是我们的总大小，因为相比较于原数组，我们引入了一个箱子的概念，那么除了箱子数，我们还需要记录每个箱子的大小，所以需要有一个数来记录箱子大小，这里注意我们规定盛装大小不超过256bit，因此箱子大小值最大不超过2^8，即箱子大小值占用不超过8bit，因此总共的大小是48bit+8bit = 56bit.
实际上如果存储2也用8个字节显然是浪费的，2的8次方式256，在进行一次分组，[73,227]放一组，[2,30,11,29]再放一组。
[73,227]存储需要几个字节呢？2的8次方是大于最大的227的，记录箱子大小是需要一个字节的，73,227需要2个字节一共是3个字节；
[2,30,11,29]，2的5次方32是大于29的，所以四个数需要20个比特位，共三个字节存储，存储箱子大小在需要一个字节，共4个字节。
所以经过for算法进行压缩，共7个字节就可以存储，压缩前是需要24个字节的，明显效率提高。
可以看到大小又变小了，但是思考一个问题：是不是还可以进行压缩？是越小越好吗？
是可以再压缩，但是我们还要考虑解码的问题，数据压缩后是要使用的，因此需要解码，压缩得越深，解码越耗时，因此不是越小越好，那么在哪里取一个平衡，这就是通过计算机动态计算的，计算方法这里不做深一步讨论了，大家理解这个概念即可
以上就是FOR算法的概念，总结一下：
（1）数组元素值为与前一位的差值V(n)=V(n)-V(n-1)，n=2,3,4…
（2）计算数组中最大值所需占用的大小
（3）计算数组是否需要拆分，计算拆分后每组的最大值所需占用的大小并记录

RBM算法(RoaringBitMap)
有了FOR算法为什么需要别的算法呢？说明FOR算法本身是有缺陷的，那么思考一下FOR算法的缺陷在哪里？
FOR算法的核心是用减法来缩减数值大小，但是减法一定能缩减大小吗？但数值大小很大时，减法能够达到的效果是不明显的，比如100W,200W,300W,相减后是100W,100W,100W，依然很大，这时的压缩效果很不理想，所以引入了RBM算法

那么大家再思考一下，既然减法不能满足，那么还有什么方法能够更快地减小数值大小呢？
没错，就是除法！

RBM的核心就是通过除法来缩减数值大小，但是并不是直接的相除。
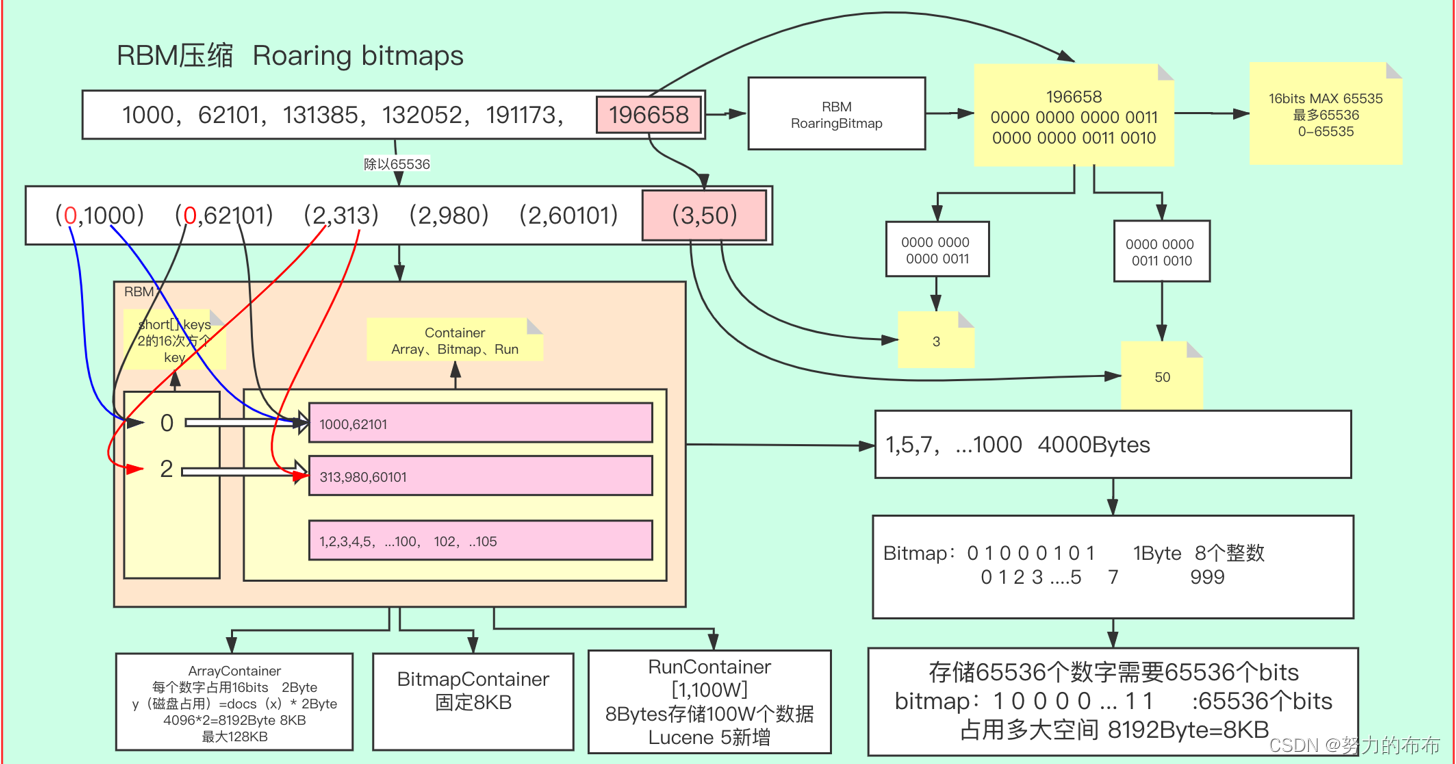
比如数组为1000,62101,131385,191173,196658
其中196658的二进制表示为0000 0000 0000 0011 0000 0000 0011 0010
然后将其高16位和低16位分别转换为10进制：
0000 0000 0000 0011 -> 3
0000 0000 0011 0010 -> 50
那么196658就转换成了(3,50)的表示形式，其效果就相当于除以2^16,商3余50

这里的计算用位运算会更快更好理解，除以2^n相当于将这个数的二进制向右位移n位（不含符号位）,并且用0补足空位。容易得出196658二进制右移16位后为
0000 0000 0000 0000 0000 0000 0000 0011
也就是其高16位，前面用0补足，而被位移顶替掉的就是其余数0000 0000 0011 0010

因为商和余数都不超过16位，那么我们最大用16bit来存储足够了。也就是short类型，占用2个字节。因此商和余数都可以用一个short来盛装，那么所有的商就是一个short[]，所有的余数就是一个short[][]将原数组除以2^16得：
(0,1000),(0,62101),(2,313),(2,980),(2,60101),(3,50)
转化为二维数组盛装
0: 1000,62101
2: 313,980,60101
3: 50

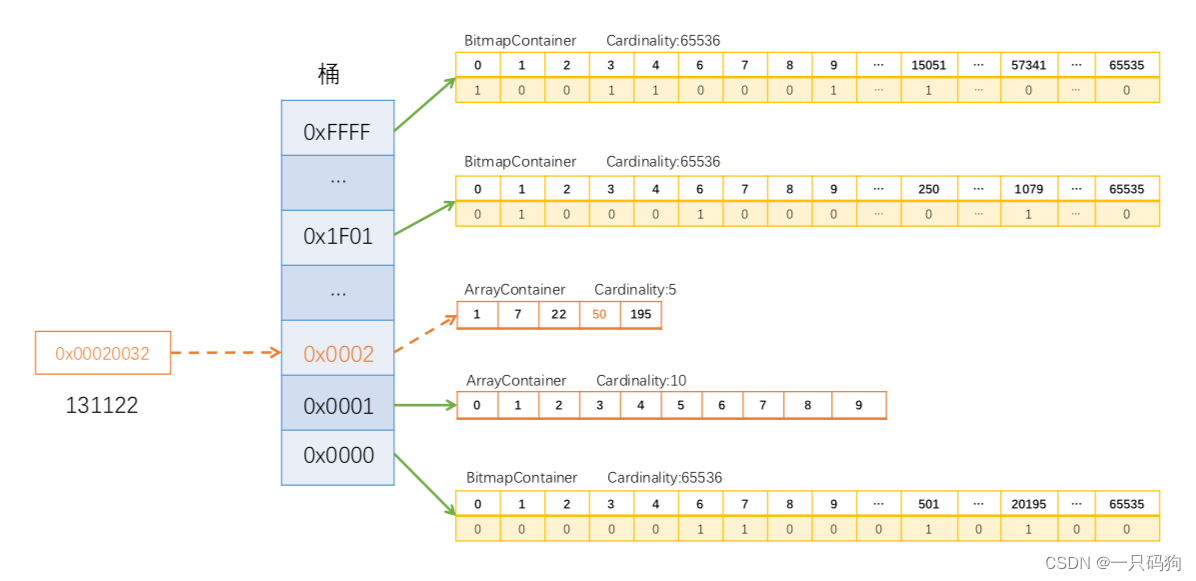
我们把每一个商所对应的余数short[]称之为一个容器Container，使用上述所说的short盛装也称为ArrayContainer

我们也容易观察发现到，每一个Container实际上都是有序数值数组，是不是能够联想到什么？
数组还能进行压缩吗？
数组能用FOR算法再压缩吗？
有别的方式再进行压缩吗？

首先回答前两个问题：数组肯定可以压缩，而且正是我们需要去做的；用FOR算法在这里进行压缩是可以的，不算错，但是我们说不合适，正如在FOR算法中介绍的那样，压缩的同时我们还有考虑解码时的效率，其实这里已经经过除法做了一次处理了，那么再用减法做一次处理，再解码时效率会降低不少，所以我们追求的是一种解码更加容器，但又能具备压缩能力的方法。
因此我们就可以使用bitmap来存储数据，按照规定一个Container的最大值是65534（这里为什么最大值是65534，思考一下，如果不明白往上看看原数组是怎么处理的）,也就需要65535bit=8k的容器来存储，当然bitmap有个很明显的缺点，那就是无论Container中有多少个数，都要占用8k的大小，所以当数量不超过65535bit /16bit = 4096个时，使用short (16bit)来存储更划算，当每个Container的数量超过4096个时使用bitmap更加划算，那么使用bitmap的Container称为BitmapContainer

 

 

进行一个小小的总结，RBM的算法核心就是把数据表示成2进制共32位，分为高16和低16.分别存储，所以最大就是2的16次方65536,65536。
如果用short存储，需要65536个short数据类型就是65536x2byte再除以1024就是128KB。
如果用BitMapContainer存储，需要的是65536个比特位，当前索引有数据就是1没有就是0，还是用二进制01表示，65536比特位除以8是8192个比特再除以1024就是8KB。
用数组short最大是128KB，bitmap最大是8KB且固定。
再算一下，8KB可以存储多少个short类型的数据，8x1024=8192个byte，8192除以2是4096表示可以存储4096个short数组，所以低于4096用short存储比较节省空间，高于4096用bitmap比较好节省空间。

 

RBM算法的核心步骤如下：
（1）数组中每个数除以2^16，以商,余数的形式表示出来
（2）将相同商的归在一个Container，如果Contaniner中数值容量超过4096使用bitmap的形式来存储一个Container中的数，如果没有超过那就使用short[]来存储，如果是连续数组那就使用RunContainer来存储

————————————————
版权声明：本文为CSDN博主「努力的布布」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_37200262/article/details/125020146

参考

https://blog.csdn.net/wlei0618/article/details/125846561

文档

https://www.elastic.co/guide/cn/elasticsearch/guide/2.x/_combining_the_two.html