第二章 信息的表示和处理（下）

2.2及2.3 整数表示及整数运算

无符号数：给定一个整数，假设其二进制长度有w位，那么这w位每一位的值都取0或1，每一位都表示数值；

有符号数：它与无符号数的区别，w位二进制值，第一位表示符号位，0表示整数，1表示负数，后面w-1位表示数值；

原码：符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值

反码：

正数的反码是其本身

负数的反码是在其原码的基础上, 符号位不变，其余各位取反

补码：

正数的补码就是其本身 

负数的补码是在反码的基础上+1；

 

举例：给定值-8，求其原码、反码、补码值

原码：10001000

反码：11110111

补码：11111000

 

2.4 浮点数

二进制小数：

如：

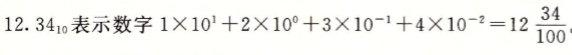
浮点数：相比整数类型，浮点数的特点是能表示的数的范围更大，但是无法保证能精确表示。最常见的单精度和双精度格式如下图：

 

 

浮点数：

浮点数的加减乘除运算：两个数值实际的运算结果再舍入一下。

浮点数的加法和乘法，不一定不满足结合律，比如(3.14+1e10)-1e10的计算结果为0（3.14被舍掉了），但是3.14+(1e10-1e10)的计算结果为3.14。

关于int和float和double之间的转换，主要就是int转到double能完全保留precision（精度）和range；而int转到float却不能，所以可能会有舍入，但不会有溢出。