4.5 最大流

一.最大流的简介

1.输入：一个边赋权（边的容量为正数）有向图，具有一个开始顶点s和目标顶点t

2.最小割问题：

（1）st-割（切分）是将顶点划分为2个不相交的集合，s在集合A，t在另一个集合B

（2）st割的容量是从A到B的边的集合之和（不用计算B到A的边）。

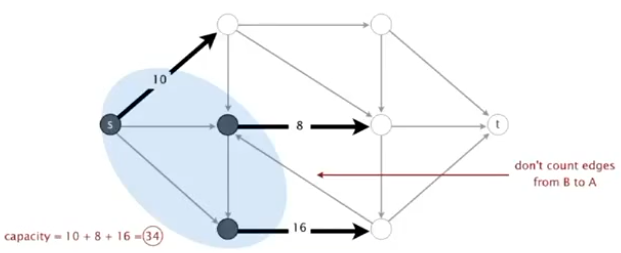
（3）最小割：找到容量最小的st-切分

3.最大流问题

（1）st流是对边的流量的一种分配，满足：

①容量限制：0≤边的流≤边的容量

②局部相等：对于每个点来说（除了s和t）输入流=输出流

（2）流的值是t的输入流

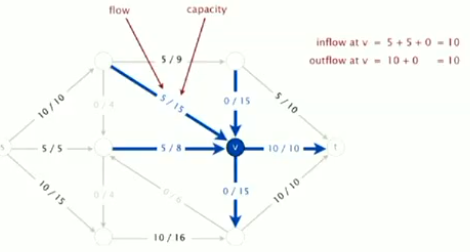
（3）最大流：找到流的最大值

4.增广路径：寻找s-t的无向的路径，满足

（1）可以在forward edges（路径方向和箭头方向相同）上增加流，不能满

（2）可以在backward edges（路径方向和箭头方向相反）上减小流，不能空

终止条件：s到t的所有路径都被阻塞：要么，forward edges满了；要么backward edges空了

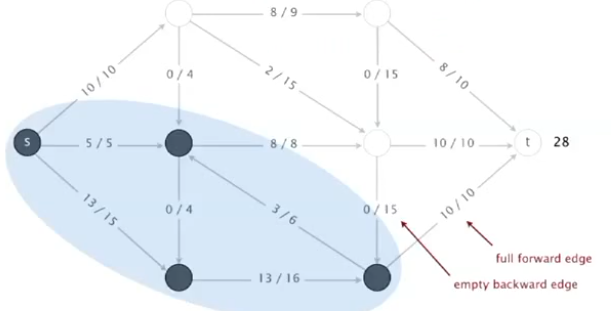
5.Ford-Fulkerson算法：各边从流为0开始，当存在增广路径时，进行如下操作：

（1）找到一条增广路径

（2）计算瓶颈容量

（3）使用瓶颈容量增加那条路径上的流

6.st-切分的跨切分流量（net flow across）cut(A,B)是切分的所有A到B的边的流之和减去切分的所有从B到A的边的流之和。

7.最大流量-最小切分定理。令f为一个st-流量网络，以下三种条件是等价的：

（1）存在某个st-切分，其容量和f的流量相等

（2）f达到了最大流量

（3）f中不存在任何增广路径

8.由最大流f得到最小割（A，B）：

（1）根据增广路径定理，没有关于f的增广路径

（2）集合A=set of vertices connected to s by  an undirected path with no full forward  or empty backward edges（中文不好翻译，英文比较容易理解）

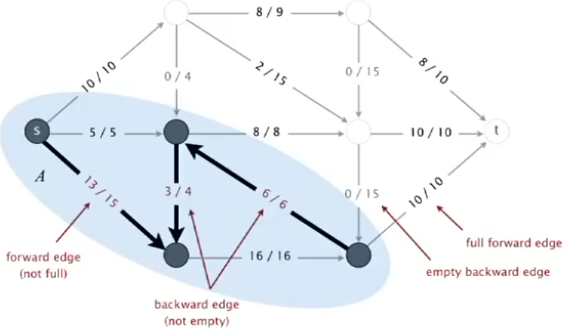
9.一些思考

（1）如何计算一个最小割？由上面的分析，计算出最大流，最小割很容易得到

（2）如何找到增广路径？ BFS能够很好的解决

（3）如果FF能够终止，总能计算一个最大流吗？ 对

（4）FF算法总是能够终止吗？（需要边的容量是整数或者仔细选择增广路径）。如果是，需要多少次增广操作？（需要很好的分析）

10.结论:当所有容量是整数时，存在一个整数值得最大流量，并且FF算法可以找到这个最大值。

11.分析

（1）即使边的容量是整数，增广路径的数量也有可能等于最大流的大小，也就是需要很多次。如下图所示，如果增广路径没有找好，需要200次寻找增广矩阵的过程，我们希望避免这种情况。

。。。。

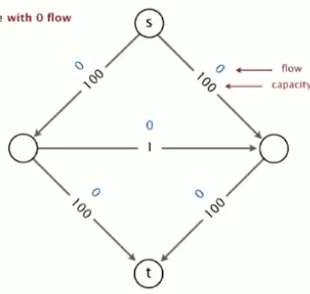
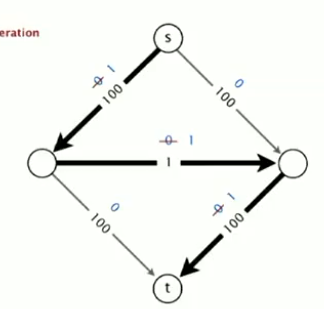
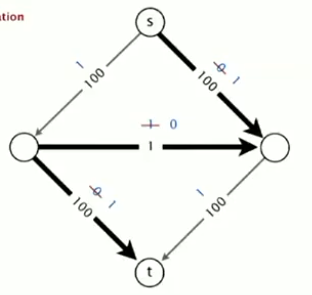（2）幸运的是，可以很容易的避免上述的情况，比如使用shortest/fattest path。

（3）也就是说，FF的性能取决于增广路径的选择，下面给出了一些可能的选择策略

shortest path是取边的数量最小的路径，fattest path 是取瓶颈容量最大边的路径。上面只是指出了上界，在实际中，这几种策略的性能很好。

12.边的表示，这里每条边e=v->w需要指定起点v和终点w，并给出流fe和容量ce

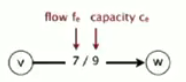
package com.cx.graph;

public class FlowEdge {
    private final int v,w;
    //边的容量
    private final double capacity;
    //边的流量
    private double flow;

    private FlowEdge(int v, int w, double capacity) {
        this.v = v;
        this.w = w;
        this.capacity = capacity;
    }
    public int from()  {return v;}
    public int to() { return w;}
    public double capaciity() {return    capacity;}
    public double flow() { return flow;}
    
    public int other(int vertex) {
        if(vertex==v) return w;
        else if(vertex == w) return v;
        else throw new RuntimeException("Illegal endpoint");
    }
    //边的剩余容量
    public double residualCapacityTo(int vertex) { 
        //w->v
        if(vertex==v) return flow;
        //v->w
        else if(vertex==w) return capacity-flow;
        else throw new IllegalArgumentException();
    }
    //将边的流量增加delta
    public void addResidualFlowTo(int vertex,double delta) {
        //w->v
        if(vertex==v) flow-=delta;
        //v->w
        else if(vertex==w) flow+=delta;
        else throw new IllegalArgumentException();
    }
}

13.流网络的表示，需要在两个方向上处理边e=v->w，因此需要将e同时放在v和w的邻域列表中。

14.剩余容量：

（1）对于前向边v->w来说：剩余容量=ce-fe

（2）对于后向边w->v来说：剩余容量=fe

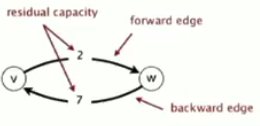
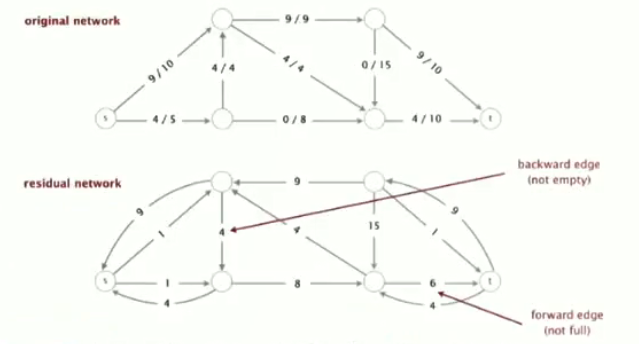
15.剩余网络：根据上面剩余容量的定义，可以将原始网络改写为剩余网络的形式，利于分析。

原始网络中的增广路径等价于剩余网络中的带方向的路径。也就可以使用以前有向图的算法来获得一条增广路径。

package com.cx.graph;

import edu.princeton.cs.algs4.Bag;

public class FlowNetwork {
    private final int V;
    private Bag<FlowEdge>[] adj;
    
    public FlowNetwork(int V) {
        this.V=V;
        adj=(Bag<FlowEdge>[])new Bag[V];
        for(int v=0;v<V;v++) {
            adj[v]=new Bag<FlowEdge>();
        }
    }
    public void addEdge(FlowEdge e) {
        int v=e.from();
        int w=e.to();
        //添加前向边
        adj[v].add(e);
        //添加后向边
        adj[w].add(e);
    }
    public Iterable<FlowEdge> adj(int v){
        return adj(v);
    }
}

16.FF算法的代码实现：

package com.cx.graph;

import edu.princeton.cs.algs4.Queue;

public class FordFulkerson {
    //在剩余网络中是否存在s->v的路径
    private boolean[] marked;
    //s->v路径的最后一条边
    private FlowEdge[] edgeTo;
    //流的值
    private double value;

    public FordFulkerson(FlowNetwork G,int s,int t) {
        value=0;
        while(hasAugmentingPath(G,s,t)) {
            double bottle=Double.POSITIVE_INFINITY;
            for(int v=t;v!=s;v=edgeTo[v].other(v))
                bottle=Math.min(bottle, edgeTo[v].residualCapacityTo(v));
            for(int v=t;v!=s;v=edgeTo[v].other(v))
                edgeTo[v].addResidualFlowTo(v, bottle);
            value+=bottle;
        }
    }
    public boolean hasAugmentingPath(FlowNetwork G,int s,int t) {
        marked=new boolean[G.V()];
        edgeTo=new FlowEdge[G.V()];
        
        Queue<Integer> q=new Queue<Integer>();
        q.enqueue(s);
        marked[s]=true;
        while(!q.isEmpty()) {
            int v=q.dequeue();
            for(FlowEdge e:G.adj(v)) {
                int w=e.other(v);
                if(e.residualCapacityTo(w)>0 && !marked[w]) {
                    edgeTo[w]=e;
                    marked[w]=true;
                    q.enqueue(w);
                }
            }
        }
        return marked[t];
    }
    public double value() { return value;}
    public boolean inCut(int v) { return marked[v];}
}