树形DP
树型动态规划就是在“树”的数据结构上的动态规划。
从一个例题开始吧:
hdu 1520
一棵有根树上,每个结点有一个权值。相邻的父结点和子结点只能选择一个,问如何选择,使得总权值之和最大。(邀请员工参加宴会,为了避免员工和直属上司发生尴尬,规定员工和直属上司不能同时出席。)
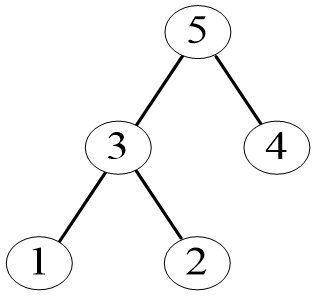
定义状态:
dp[i][0]:不选择当前结点的最优解;
dp[i][1]:选择当前结点时的最优解。
状态转移方程,有两种情况:
(1)不选择当前结点,那么它的子结点可选可不选,取其中的最大值:
dp[u][0] += max(dp[son][1], dp[son][0])
(2)选择当前结点,那么它的子结点不能选:dp[u][1] += dp[son][0];
程序包含三个部分:
(1)建树。本题可以用STL的vector 生成链表,建立关系树。
(2)树的遍历。可以用DFS,从根结点开始进行记忆化搜索。
(3)DP。
复杂度:O(n)
#include <bits/stdc++.h> using namespace std; const int N=6005,inf=0x3f3f3f;; int value[N],fa[N]; vector<int> tree[N]; int f[N][2],n,a,b; void dfs(int u) { f[u][0]=0;//初始化,不选当前节点 f[u][1]=value[u];//选当前节点的初始化 for(int i=0;i<tree[u].size();i++){ int son=tree[u][i]; dfs(son); f[u][0]+=max(f[son][1],f[son][0]);//儿子可以取也可以不取 f[u][1]+=f[son][0]; } } int main() { while(cin>>n){ for(int i=1;i<=n;i++){//存入节点权值、初始化 scanf("%d",&value[i]); tree[i].clear(); fa[i]=-1; } while(cin>>a>>b){//存入父子关系 if(!a&&!b) break; tree[b].push_back(a);//邻接表形式 fa[a]=b; } int root=1; while(fa[root]!=-1) root=fa[root];//找根节点 dfs(root);//遍历 printf("%d\n",max(f[root][1],f[root][0]));//根节点的取和不取当中找最大值 } return 0; }
hdu 2196 “Computer”
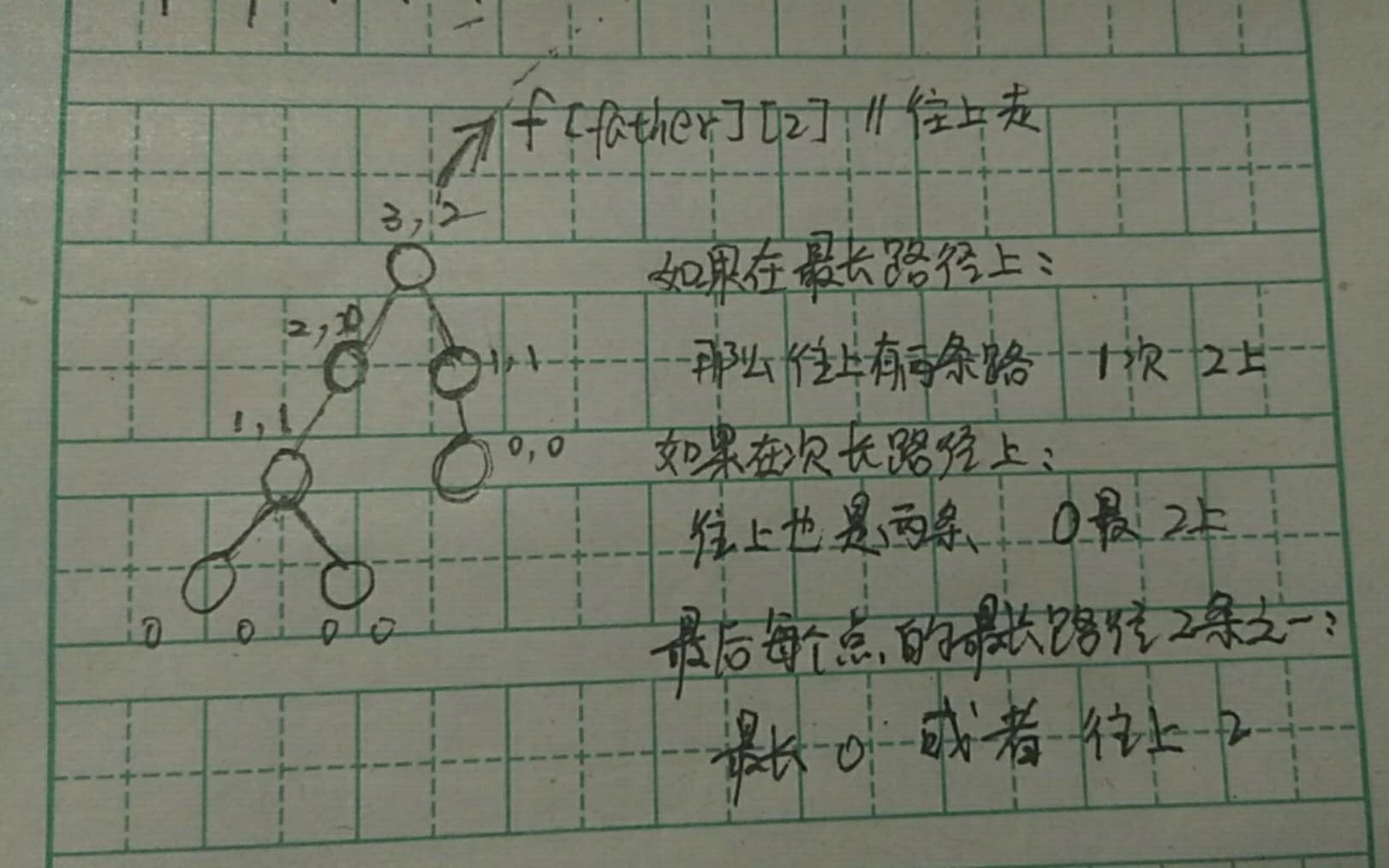

#include <bits/stdc++.h> using namespace std; const int N=10005,inf=0x3f3f3f; struct node{ int id,cost; }; vector<node> tree[N]; int f[N][3],n; void init() { for(int i=1;i<=n;i++) tree[i].clear(); memset(f,0,sizeof(f)); for(int i=2;i<=n;i++) { int x,y;scanf("%d %d",&x,&y); node tmp;tmp.id=i;tmp.cost=y; tree[x].push_back(tmp); } } void dfs1(int father) { int one=0,two=0; for(int i=0;i<tree[father].size();i++){ node child=tree[father][i]; dfs1(child.id); int cost=f[child.id][0]+child.cost; if(cost>=one){two=one;one=cost;}//noe记录最长距离,two记录次长距离 if(cost<one&&cost>two) two=cost; } f[father][0]=one;f[father][1]=two; } void dfs2(int father) { for(int i=0;i<tree[father].size();i++){ node child=tree[father][i]; if(f[child.id][0]+child.cost==f[father][0])//child 就在最长距离的子树上 f[child.id][2]=max(f[father][2],f[father][1])+child.cost; else f[child.id][2]=max(f[father][2],f[father][0])+child.cost; dfs2(child.id); } } int main() { while(cin>>n){ init(); dfs1(1);//题目规定1为根节点 f[1][2]=0;//往上走的距离 dfs2(1); for(int i=1;i<=n;i++){ printf("%d\n",max(f[i][0],f[i][2])); } } return 0; }
1575:【例 1】二叉苹果树(由根分为左子树和右子树的情况)

【题目描述】 有一棵二叉苹果树,如果数字有分叉,一定是分两叉,即没有只有一个儿子的节点。这棵树共 NN 个节点,标号 11 至 NN,树根编号一定为 11。 我们用一根树枝两端连接的节点编号描述一根树枝的位置。一棵有四根树枝的苹果树,因为树枝太多了,需要剪枝。但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留住多少苹果。 【输入】 第一行两个数 NN 和 QQ ,NN 表示树的节点数,QQ 表示要保留的树枝数量。 接下来 N−1N−1 行描述树枝信息,每行三个整数,前两个是它连接的节点的编号,第三个数是这根树枝上苹果数量。 【输出】 输出仅一行,表示最多能留住的苹果的数量。 【输入样例】 5 2 1 3 1 1 4 10 2 3 20 3 5 20 【输出样例】 21 【提示】 数据范围与提示: 对于 100% 的数据,1≤Q≤N≤100,N≠11≤Q≤N≤100,N≠1,每根树枝上苹果不超过 3000030000 个。
思路:首先树根是肯定要保留的,保留Q条边,那么一定要保留Q+1个节点,此时可以用状态 f[i][j] 表示以i为根节点的树保留 j 个节点时的最大权值;此时有状态转移方程:
f[i][j]=max(f[i][j],f[l[i]][k]+f[r[i]][j-k-1]+a[i]);

//yrnddup c++ code //状态转移方程:f[i][j]=max(f[i][j],f[l[i]][k]+f[r[i]][j-k-1]+a[i]); #include <bits/stdc++.h> using namespace std; const int N=105,inf=0x3f3f3f; int l[N],r[N],f[N][N],Map[N][N],a[N],n,q; void buildtree(int fa) { for(int i=1;i<=n;i++)//建立左子树 { if(Map[fa][i]>=0) { l[fa]=i;a[i]=Map[fa][i]; Map[fa][i]=-1;Map[i][fa]=-1;//标记访问 buildtree(i); break; } } for(int i=1;i<=n;i++)//建立右子树 { if(Map[fa][i]>=0) { r[fa]=i;a[i]=Map[fa][i]; Map[fa][i]=-1;Map[i][fa]=-1;//标记访问 buildtree(i); break; } } } int dfs(int i,int j) { if(j==0) return 0; if(l[i]==0&&r[i]==0) return a[i];//叶子节点 if(f[i][j]>0) return f[i][j];//记忆化处理 for(int k=0;k<=j-1;k++) f[i][j]=max(f[i][j],dfs(l[i],k)+dfs(r[i],j-k-1)+a[i]); return f[i][j]; } int main() { cin>>n>>q;q++; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) Map[i][j]=-1;//初始化 for(int i=1;i<n;i++) { int x,y,z; cin>>x>>y>>z; Map[x][y]=Map[y][x]=z; } buildtree(1);//以1为根节点建立二叉树 cout<<dfs(1,q)<<endl; return 0; }
1576:【例 2】选课(背包类树形DP)
其实就相当于某一门课程的先修课为他的父节点,那么在选择子节点前肯定已经选过父节点了,那么整个课程的关系就是一片森林,所以这个时候我们就要虚拟一个0号节点作为所有森林的根节点就变成了一棵树了
这个时候我们与前面的做法相似;用f[i][j]表示以i作为节点的选择j个节点的最优值

Description 学校实行学分制。每门的必修课都有固定的学分,同时还必须获得相应的选修课程学分。学校开设了N(N<300)门的选修课程,每个学生可选课程的数量M是给定的。学生选修了这M门课并考核通过就能获得相应的学分。 在选修课程中,有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其它的一些课程的基础上才能选修。例如《Frontpage》必须在选修了《Windows操作基础》之后才能选修。我们称《Windows操作基础》是《Frontpage》的先修课。每门课的直接先修课最多只有一门。两门课也可能存在相同的先修课。每门课都有一个课号,依次为1,2,3,…。 例如: 表中1是2的先修课,2是3、4的先修课。如果要选3,那么1和2都一定已被选修过。 你的任务是为自己确定一个选课方案,使得你能得到的学分最多,并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。 Input 第一行有两个整数N,M用空格隔开。(1<=N<=300,1<=M<=200)。 以下N行每行代表一门课。课号依次为1,2,…,N。每行有两个数(用一个空格隔开),第一个数为这门课先修课的课号(若不存在先修课则该项为0),第二个数为这门课的学分。学分是不超过10的正整数。 Output 只有一行,选M门课程的最大得分。 Sample Input 7 4 2 2 0 1 0 4 2 1 7 1 7 6 2 2 Sample Output 13

#include <bits/stdc++.h> using namespace std; const int N=305,inf=0x3f3f3f; vector<int>son[N]; int f[N][N],a[N],n,m; void dp(int x) { f[x][0]=0; for(int i=0;i<son[x].size();i++) { int y=son[x][i]; dp(y); for(int t=m;t>=0;t--) for(int j=t;j>=0;j--) f[x][t]=max(f[x][t],f[x][t-j]+f[y][j]); } if(x!=0) for(int t=m;t>=0;t--) f[x][t]=f[x][t-1]+a[x]; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { int x; cin>>x>>a[i]; son[x].push_back(i); } memset(f,0xcf,sizeof(f));//-inf,相当于207 dp(0);//虚拟的0号节点 cout<<f[0][m]<<endl; return 0; }
1577:【例 3】数字转换(树的最长链)
其实就是求树的最长链,就把给出的数以内的所有树的约数和求出来,能够互相转换的就有一条边,把所有的关系连起来,找到其中最长的一条路径就okk了
但是计算的过程不长,比较巧妙,但是动态规划的难道就是最长和次长的哪里么,不是很容易想到

【题目描述】 如果一个数 xx 的约数和 yy (不包括他本身)比他本身小,那么 xx 可以变成 yy,yy 也可以变成 xx。例如 44 可以变为 33,11 可以变为 77。限定所有数字变换在不超过 nn 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。 【输入】 输入一个正整数 nn。 【输出】 输出不断进行数字变换且不出现重复数字的最多变换步数。 【输入样例】 7 【输出样例】 3 【提示】 样例说明 一种方案为 4→3→1→74→3→1→7。 数据范围与提示: 对于 100% 的数据,1≤n≤500001≤n≤50000。

#include <bits/stdc++.h> using namespace std; const int N=50005,inf=0x3f3f3f; int n,sum[N],dis1[N],dis2[N],ans; void dp() { for(int i=n;i>=1;i--)//大数字为小数字的后代 { if(sum[i]<i)//i为sum[i]的后代 if(dis1[i]+1>dis1[sum[i]])//距离更新 { dis2[sum[i]]=dis1[sum[i]];//次长 dis1[sum[i]]=dis1[i]+1; //最长 } else if(dis1[i]+1>dis2[sum[i]]) dis2[sum[i]]=dis1[i]+1; } } int main() { cin>>n; for(int i=1;i<=n;i++) for(int j=2;j<=n/i;j++) sum[i*j]+=i;//用这种方式求约数和也是可 dp();//相当于建树 for(int i=1;i<=n;i++) ans=max(ans,dis1[i]+dis2[i]); cout<<ans<<endl; return 0; }
1578:【例 4】战略游戏(求树的最大独立集)
这个题目主要就是会考虑两个状态;放和不放两种情况
放的话;孩子节点可放可不放,就取这两种情况的最小值,
不放,那么所有的子节点都必须要放
f[x][0]+=f[node[x].child[i]][1];
f[x][1]+=min(f[node[x].child[i]][1],f[node[x].child[i]][0]);

【题目描述】 Bob 喜欢玩电脑游戏,特别是战略游戏。但是他经常无法找到快速玩过游戏的方法。现在他有个问题。 现在他有座古城堡,古城堡的路形成一棵树。他要在这棵树的节点上放置最少数目的士兵,使得这些士兵能够瞭望到所有的路。 注意:某个士兵在一个节点上时,与该节点相连的所有边都将能被瞭望到。 请你编一个程序,给定一棵树,帮 Bob 计算出他最少要放置的士兵数。 【输入】 输入数据表示一棵树,描述如下。 第一行一个数 NN ,表示树中节点的数目。 第二到第 N+1N+1 行,每行描述每个节点信息,依次为该节点编号 ii,数值 kk,kk 表示后面有 kk 条边与节点 ii 相连,接下来 kk 个数,分别是每条边的所连节点编号 r1,r2,⋯,rkr1,r2,⋯,rk 。 对于一个有 NN 个节点的树,节点标号在 00 到 N−1N−1 之间,且在输入文件中每条边仅出现一次。 【输出】 输出仅包含一个数,为所求的最少士兵数。 【输入样例】 4 0 1 1 1 2 2 3 2 0 3 0 【输出样例】 1 【提示】 数据范围与提示: 对于 100% 的数据,有 0<N≤15000<N≤1500。

#include <bits/stdc++.h> using namespace std; const int N=1505,inf=0x3f3f3f; struct di{ int num,child[N]; }node[N]; int f[N][2],a[N],n; void dp(int x) { f[x][1]=1;f[x][0]=0; if(node[x].num==0) return;//叶子节点的情况 for(int i=1;i<=node[x].num;i++) { dp(node[x].child[i]); f[x][0]+=f[node[x].child[i]][1]; f[x][1]+=min(f[node[x].child[i]][1],f[node[x].child[i]][0]); } } int main() { cin>>n; for(int i=1;i<=n;i++) { int x; scanf("%d",&x); scanf("%d",&node[x].num); for(int j=1;j<=node[x].num;j++) { int y; scanf("%d",&y);node[x].child[j]=y; a[y]=1; } } int root=0; while(a[root]) root++; dp(root); printf("%d\n",min(f[root][0],f[root][1])); return 0; }
1579: 【例 5】皇宫看守(普通树的动态规划问题)

【题目描述】 太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。 皇宫以午门为起点,直到后宫嫔妃们的寝宫,呈一棵树的形状,某些宫殿间可以互相望见。大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。 可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。 帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。 【输入】 输入中数据描述一棵树,描述如下: 第一行 nn,表示树中结点的数目。 第二行至第 n+1n+1 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 i(0<i≤n)i(0<i≤n),在该宫殿安置侍卫所需的经费 kk,该边的儿子数 mm,接下来 mm 个数,分别是这个节点的 mm 个儿子的标号r1,r2,⋯,rmr1,r2,⋯,rm 。 对于一个 nn 个结点的树,结点标号在 11 到 nn 之间,且标号不重复。 【输出】 输出最少的经费 【输入样例】 6 1 30 3 2 3 4 2 16 2 5 6 3 5 0 4 4 0 5 11 0 6 5 0 【输出样例】 25 【提示】 样例解释: 有六个区域被安排的情况如左图所示。 如右图,灰色点安排了警卫,22 号警卫可以观察 1,2,5,61,2,5,6,33 号警卫可以观察 1,31,3,44 号警卫可以观察 1,41,4。 总费用:16+5+4=2516+5+4=25 数据范围与提示: 对于 100% 的数据,0<n≤15000<n≤1500。
三种状态(不要问我为什么):
f[i][0]表示为i节点在父节点可以看到,以i为根的子树需要安排的最少士兵数
f[i][1]表示为i节点在子节点可以看到时,以i为根的子树需要安排的最少士兵数
f[i][2]表示为在i节点安排警卫时,以i为根的子树需要安排的最少士兵数
对于定义的这三种状态,我们来挨个进行分析
1、父节点可以看到的时候,该节点的子节点要么安排警卫要么被子节点看到
2、子节点可以看到时,其他子节点要么安排警卫要么被他们的子节点看到
3、该节点安排了警卫时,则它的子节点要么安排警卫,要么子节点的父节点安排警卫,要么子节点的子节点安排警卫
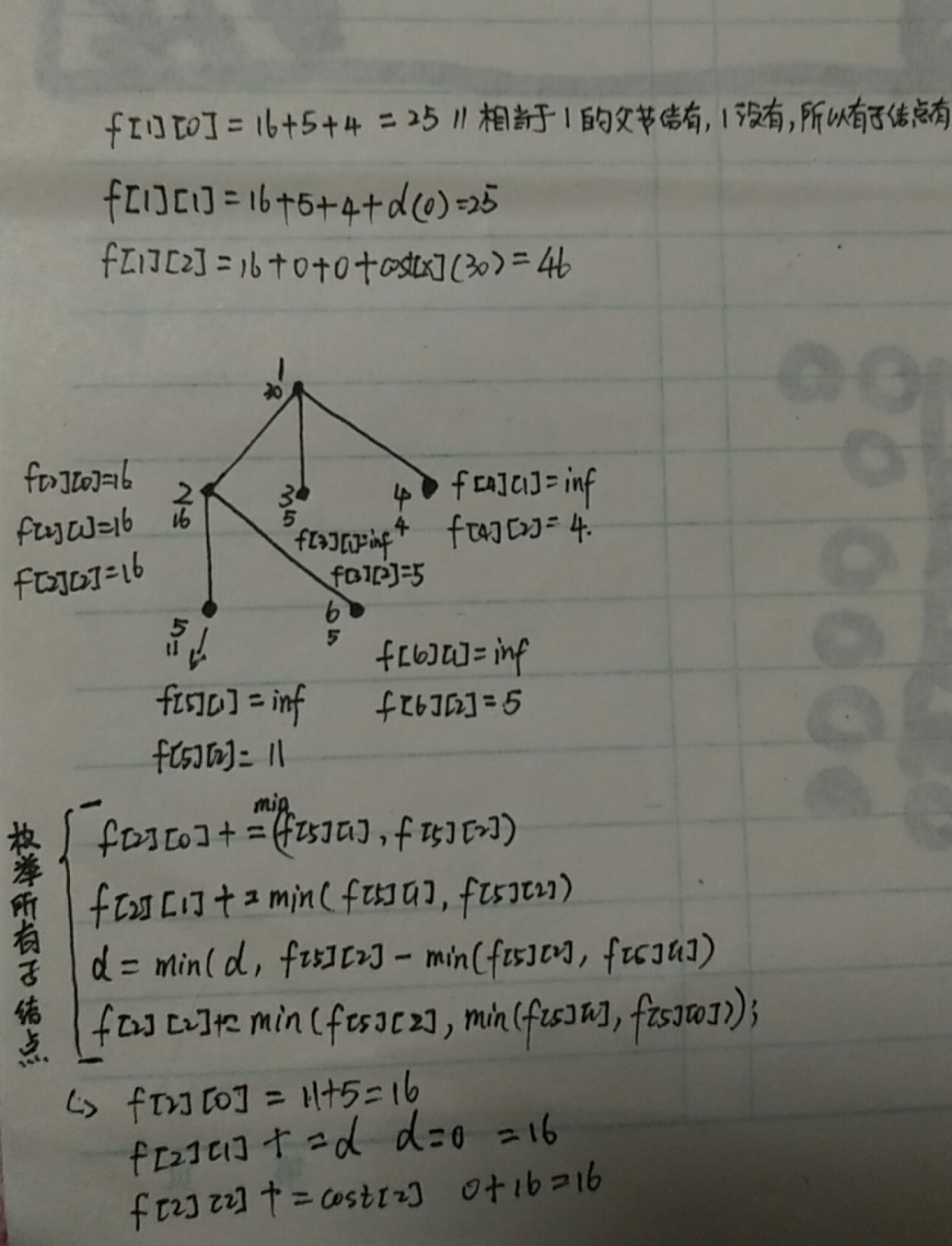

#include <bits/stdc++.h> using namespace std; const int N=2005,inf=0x3f3f3f; struct bian{ int to,next; }a[N*2]; int f[N][3],n,cou,head[N],root,vis[N],cost[N]; void addedge(int x,int y) { a[++cou].to=y;a[cou].next=head[x];head[x]=cou; } void dp(int x,int fa) { int d=inf; for(int i=head[x];i;i=a[i].next){ int y=a[i].to; if(y==fa) continue; dp(y,x); f[x][0]+=min(f[y][1],f[y][2]); f[x][1]+=min(f[y][1],f[y][2]); d=min(d,f[y][2]-min(f[y][2],f[y][1])); f[x][2]+=min(f[y][2],min(f[y][1],f[y][0])); } f[x][1]+=d; f[x][2]+=cost[x]; } void init() { cin>>n; for(int i=1;i<=n;i++) { int x,num;cin>>x; cin>>cost[x]>>num; for(int j=1;j<=num;j++) { int y;cin>>y; addedge(x,y); vis[y]=1; } } root=1; while(vis[root]) root++; } int main() { init(); memset(vis,0,sizeof(vis)); dp(root,0); cout<<min(f[root][1],f[root][2])<<endl; return 0; }
1580:加分二叉树
注意考虑中序遍历的特点,中序遍历的顺序必须为1 2 3 4 ...;那么如果以一个点为根节点的话,前面的 数字必须在左子树。
所以就有状态转移方程:
f[i][j]=max(f[i][k-1]*f[k+1][j]+f[k][k],f[i][j])

【题目描述】 原题来自:NOIP 2003 设一个 nn 个节点的二叉树 treetree 的中序遍历为 (1,2,3,⋯,n)(1,2,3,⋯,n),其中数字 1,2,3,⋯,n1,2,3,⋯,n 为节点编号。每个节点都有一个分数(均为正整数),记第 ii 个节点的分数为 didi ,treetree 及它的每个子树都有一个加分,任一棵子树 subtreesubtree(也包含 treetree 本身)的加分计算方法如下: 记 subtreesubtree 的左子树加分为 ll,右子树加分为 rr,subtreesubtree 的根的分数为 aa,则 subtreesubtree 的加分为: l×r+al×r+a 若某个子树为空,规定其加分为 11,叶子的加分就是叶节点本身的分数。不考虑它的空子树。 试求一棵符合中序遍历为 (1,2,3,⋯,n)(1,2,3,⋯,n) 且加分最高的二叉树 treetree。 要求输出: 1、treetree 的最高加分; 2、treetree 的前序遍历。 【输入】 第一行一个整数 nn 表示节点个数; 第二行 nn 个空格隔开的整数,表示各节点的分数。 【输出】 第一行一个整数,为最高加分 bb; 第二行 nn 个用空格隔开的整数,为该树的前序遍历。 【输入样例】 5 5 7 1 2 10 【输出样例】 145 3 1 2 4 5 【提示】 数据范围与提示: 对于 100% 的数据,n<30,b<100n<30,b<100,结果不超过 4×1094×109 。

//yrnddup c++ code #include <bits/stdc++.h> using namespace std; const int N=35,inf=0x3f3f3f; int f[N][N],a[N],loc[N][N]; void print(int l,int r) { if(l>r) return; cout<<loc[l][r]<<" ";//先输出根节点 print(l,loc[l][r]-1); print(loc[l][r]+1,r); } int main() { int n;cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; for(int i=1;i<=n;i++){ f[i][i]=a[i]; loc[i][i]=i;//存储根节点 } for(int len=1;len<n;len++)//节点数,相当于长度 for(int i=1;i<=n-len;i++)//起点 { int j=i+len; int x=a[j]+f[i][j-1];//j只有一课子树 f[i][j]=a[i]+f[i+1][j];//i只有一课子树的时候 loc[i][j]=i;//初始化 if(f[i][j]<x){ f[i][j]=x;loc[i][j]=j;//在这两种情况中进行比较 } for(int k=i+1;k<j;k++)//以k作为根节点 { x=a[k]+f[i][k-1]*f[k+1][j]; if(f[i][j]<x){ f[i][j]=x;loc[i][j]=k; } } } cout<<f[1][n]<<endl; print(1,n);//输出前序 return 0; }
1581:旅游规划
这个题目的思想其实也是相当于求最长链,但是这一次是需要输出最长上的点,所以在输出的时候为了不超时,输出的时候也是把最长路径加最短路径进行相加判断是否等于最大值,等于就存入点,这里还注意一下最长和次长相等的情况

【题目描述】 W 市的交通规划出现了重大问题,市政府下定决心在全市各大交通路口安排疏导员来疏导密集的车流。但由于人员不足,W 市市长决定只在最需要安排人员的路口安排人员。 具体来说,W 市的交通网络十分简单,由 nn 个交叉路口和 n−1n−1 条街道构成,交叉路口路口编号依次为 0,1,⋯,n−10,1,⋯,n−1 。任意一条街道连接两个交叉路口,且任意两个交叉路口间都存在一条路径互相连接。 经过长期调查,结果显示,如果一个交叉路口位于 W 市交通网最长路径上,那么这个路口必定拥挤不堪。所谓最长路径,定义为某条路径 p=(v1,v2,v3,⋯,vk)p=(v1,v2,v3,⋯,vk),路径经过的路口各不相同,且城市中不存在长度大于 kk 的路径,因此最长路径可能不唯一。因此 W 市市长想知道哪些路口位于城市交通网的最长路径上。 【输入】 第一行一个整数 nn; 之后 n−1n−1 行每行两个整数 u,vu,v,表示 uu 和 vv 的路口间存在着一条街道。 【输出】 输出包括若干行,每行包括一个整数——某个位于最长路径上的路口编号。为了确保解唯一,请将所有最长路径上的路口编号按编号顺序由小到大依次输出。 【输入样例】 10 0 1 0 2 0 4 0 6 0 7 1 3 2 5 4 8 6 9 【输出样例】 0 1 2 3 4 5 6 8 9 【提示】 数据范围与提示: 对于全部数据,1≤n≤2×1051≤n≤2×105 。

#include <bits/stdc++.h> using namespace std; const int N=200005,inf=0x3f3f3f; int f[N],head[N],num,n,dis1[N],dis2[N],ans,Ans[N],co,vis[N]; struct bian{ int to,next; }a[N*2]; void addedge(int x,int y) { a[++num].to=y;a[num].next=head[x];head[x]=num; } void dp(int x,int fa) { for(int i=head[x];i!=-1;i=a[i].next){ int y=a[i].to; if(y==fa) continue; dp(y,x); if(dis1[y]+1>dis1[x]){//跟前面一样,找一个最长的和一个次长路径 dis2[x]=dis1[x]; dis1[x]=dis1[y]+1; } else if(dis1[y]+1>dis2[x]) dis2[x]=dis1[y]+1; } } void work(int x,int fa,int len) { if(vis[x]==0){ Ans[++co]=x; vis[x]=1; } for(int i=head[x];i!=-1;i=a[i].next){ int y=a[i].to; if(y==fa) continue; if(dis1[y]==len-1) work(y,x,len-1); } } void dfs(int x,int fa) { if(dis1[x]+dis2[x]==ans) { if(dis1[x]!=dis2[x]) work(x,fa,dis1[x]); work(x,fa,dis2[x]); } for(int i=head[x];i!=-1;i=a[i].next){ int y=a[i].to; if(y==fa) continue; dfs(y,x); } } int main() { scanf("%d",&n); memset(head,-1,sizeof(head)); for(int i=1;i<n;i++){ int x,y; scanf("%d %d",&x,&y); addedge(x,y);addedge(y,x); } dp(0,-1);//0作为根节点 ,找到每一个点所在的最长路径和次长路径时多少 for(int i=0;i<=n-1;i++) ans=max(ans,dis1[i]+dis2[i]); dfs(0,-1); sort(Ans+1,Ans+1+co); for(int i=1;i<=co;i++) cout<<Ans[i]<<endl; return 0; }




