二叉搜索树(BST)
基本概念:
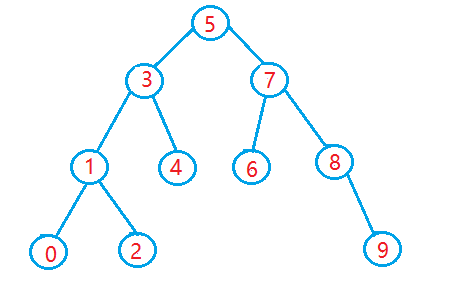
二叉搜索树又被称为二叉排序树,那么它本身也是一棵二叉树,那么满足以下性质的二叉树就是二叉搜索树:
1、若左子树不为空,则左子树上左右节点的值都小于根节点的值
2、若它的右子树不为空,则它的右子树上所有的节点的值都大于根节点的值
3、它的左右子树也要分别是二叉搜索树
例如:输入8
20 3 15 98 32 165 78 39
要求:建立二叉搜索树并中序输出(第一个输入的数其实就是根节点)
主要代码:建树:
struct tnode{
int data,right,left;
};
tnode t1[N];
cin>>n; for(int i=1;i<=n;i++) { cin>>t1[i].data; t1[i].left=t1[i].right=0; } int root=1; for(int i=2;i<=n;i++) buildtree(root,i);
void buildtree(int root,int now) { if(t1[now].data<t1[root].data){ if(t1[root].left==0) t1[root].left=now; else buildtree(t1[root].left,now); } if(t1[now].data>t1[root].data){ if(t1[root].right==0) t1[root].right=now; else buildtree(t1[root].right,now); } }
中序遍历:
void inorder(int root,tnode t[]) { if(t[root].data!=0){ inorder(t[root].left,t); cout<<t[root].data<<" "; inorder(t[root].right,t); } }
找最小、最大值:
void findmin(int root) { if(t1[root].left) findmin(t1[root].left); else cout<<root<<":"<<t1[root].data<<endl; } void findmax(int root) { if(t1[root].right) findmax(t1[root].right); else cout<<root<<":"<<t1[root].data<<endl; }
找具体的值:
void find(int root,int x) { if(root==0) { cout<<-1<<endl; return; } if(t1[root].data==x) { cout<<root<<endl;return; } else if(x<t1[root].data) find(t1[root].left,x); else if(x>t1[root].right) find(t1[root].right,x); }
完整代码:

#include <bits/stdc++.h> using namespace std; const int N=205; struct tnode{ int data,right,left; }; tnode t1[N]; int n; void buildtree(int root,int now) { if(t1[now].data<t1[root].data){ if(t1[root].left==0) t1[root].left=now; else buildtree(t1[root].left,now); } if(t1[now].data>t1[root].data){ if(t1[root].right==0) t1[root].right=now; else buildtree(t1[root].right,now); } } void inorder(int root,tnode t[]) { if(t[root].data!=0){ inorder(t[root].left,t); cout<<t[root].data<<" "; inorder(t[root].right,t); } } void findmin(int root) { if(t1[root].left) findmin(t1[root].left); else cout<<root<<":"<<t1[root].data<<endl; } void findmax(int root) { if(t1[root].right) findmax(t1[root].right); else cout<<root<<":"<<t1[root].data<<endl; } void find(int root,int x) { if(root==0) { cout<<-1<<endl; return; } if(t1[root].data==x) { cout<<root<<endl;return; } else if(x<t1[root].data) find(t1[root].left,x); else if(x>t1[root].right) find(t1[root].right,x); } int main() { cin>>n; for(int i=1;i<=n;i++) { cin>>t1[i].data; t1[i].left=t1[i].right=0; } int root=1; for(int i=2;i<=n;i++) buildtree(root,i); inorder(root,t1); cout<<endl; findmin(root); findmax(root); int x; cin>>x; find(root,x);//找指定值 return 0; } /* 8 20 3 15 98 32 165 78 39 */
其实还有几种做法:
二维数组做法:

#include <bits/stdc++.h> using namespace std; const int N=10001; int nx,rt,ch[N][2],t[N];//0是左儿子,1是右儿子 void buildtree(int &r,int x) { if(!t[r]){ r=++nx;t[r]=x; return ; } if(x>t[r]) buildtree(ch[r][1],x); else buildtree(ch[r][0],x); } void inorder(int r) { if(ch[r][0]) inorder(ch[r][0]); cout<<t[r]<<" "; if(ch[r][1]) inorder(ch[r][1]); } void findmax(int r) { if(ch[r][1]) findmax(ch[r][1]); else cout<<t[r]<<endl; } void findmin(int r) { if(ch[r][0]) findmin(ch[r][0]); else cout<<t[r]<<endl; } void find(int r,int x) { if(!t[r]) {cout<<-1<<endl;return;} if(x==t[r]) {cout<<r<<endl;return;} if(x>t[r]) find(ch[r][1],x); else find(ch[r][0],x); } int main(){ int n,a; cin>>n; for(int i=0;i<n;i++) { cin>>a; buildtree(rt,a); } inorder(rt);cout<<endl; findmax(rt); findmin(rt); cin>>a; find(rt,a); return 0; }
链表做法:(增加了删除操作)
删除操作:1、叶节点,直接删除,父节点指向空;
2、要删除的节点只有一个孩子节点,父节点指向该孩子节点
3、要删除的节点有左右两颗子树,用另一个节点替代被删除节点:右子树的最小元素或者左子树的最大元素
node *Delete(node *r,int a) { if(r==NULL) return NULL; else if(a>r->val) r->rch=Delete(r->rch,a); else if(a<r->val) r->lch=Delete(r->lch,a); else if(r->lch&&r->rch)//左右子树都在 { //node *p=new node; int p=findmax(r->lch);//找到左子树的最大值 r->val=p; r->lch=Delete(r->lch,p); } else{ node *p=new node; if(r->lch) p=r->lch; else p=r->rch; delete r; return p; } }
完整代码:

#include <bits/stdc++.h> using namespace std; const int N=10001; struct node{ int val; node *lch,*rch; }; node *insert(node *r,int a){ if(r==NULL){ node *q=new node; q->val=a; q->lch=q->rch=NULL; return q; } else if(a>r->val) r->rch=insert(r->rch,a); else r->lch=insert(r->lch,a); } void inorder(node *r) { if(r->lch) inorder(r->lch); cout<<r->val<<" "; if(r->rch) inorder(r->rch); } int findmax(node *r) { if(r->rch) return findmax(r->rch); else return r->val;//cout<<r->val<<endl; } void findmin(node *r) { if(r->lch) findmin(r->lch); else cout<<r->val<<endl; } node *Delete(node *r,int a) { if(r==NULL) return NULL; else if(a>r->val) r->rch=Delete(r->rch,a); else if(a<r->val) r->lch=Delete(r->lch,a); else if(r->lch&&r->rch)//左右子树都在 { //node *p=new node; int p=findmax(r->lch);//找到左子树的最大值 r->val=p; r->lch=Delete(r->lch,p); } else{ node *p=new node; if(r->lch) p=r->lch; else p=r->rch; delete r; return p; } } int main() { node *rt=NULL; int a,n; cin>>n; for(int i=0;i<n;i++){ cin>>a; rt=insert(rt,a); } inorder(rt); cout<<endl; //findmax(rt); //3findmin(rt); //直接删除操作 cin>>a; rt=Delete(rt,a); inorder(rt); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号