排序

冒泡排序

import random

def bubble_sort(li):
    for i in range(len(li)-1): # 一共n-1趟
        exchange = False
        for j in range(len(li)-i-1):  # 第i趟只需交换n-i-1次
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
                exchange = True
        if exchange is False:break
    return li

data = list(range(100))
data = data[::-1]
# random.shuffle(data)
print(data)
print(bubble_sort(data))

 插入排序

• 列表被分为有序区与无序区，最初有序区只有一个元素
• 每次从无序区中取出一个元素，插入到有序区的位置，直到无序区变空。

import random

def insert_sort(li):
    for i in range(1,len(li)):
        tmp = li[i]
        j = i-1
        while j>=0 and li[j]>tmp:
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp

data = list(range(100))
random.shuffle(data)
print(data)
insert_sort(data)
print(data)

 

选择排序

一趟趟遍历记录最小的数，放到第一个位置

import random

def select_sort(li):
    for i in range(len(li)-1):
        min_loc = i # 默认第i个元素为最小的
        for j in range(i+1,len(li)):
            if li[j]<li[min_loc]:
                min_loc = j
        li[i],li[min_loc] = li[min_loc],li[i]  # 一趟遍历完之后找到最小元素对应的位置min_loc之后，进行交换

data = list(range(100))
random.shuffle(data)
print(data)
select_sort(data)
print(data)

 

快速排序

• 取一个元素p，使元素p归位，[5 7 4 6 3 1 2 9 8]
• 使得列表被元素p分为两部分：左边都比p小，右边都比p大 [ 2 1 4 3 5 6 7 9 8]
• 递归完成排序

nums = [3,5,9,30,34]

def fsort(nums,l,r):
    if l >= r:
        return
    i, j = l, r
    while i < j:
        while nums[j] >= nums[l] and i < j:
            j -= 1
        while nums[i] <= nums[l] and i < j:
            i += 1
        nums[i], nums[j] = nums[j], nums[i]
    nums[i], nums[l] = nums[l], nums[i]
    fsort(nums,l, i - 1)
    fsort(nums,i + 1, r)
    return nums
print(fsort(nums,0,len(nums)-1))

 

归并排序

本质上是将两个有序列表归并为一个有序列表：[2 5 7 8 9]  [1 3 4 6]

依次去队首更小者放入新列表中

def merge(li,low,mid,high):
    i = low
    j = mid + 1
    ltemp = []
    while j <= high and i<=mid:
        if li[i] <= li[j]:
            ltemp.append(li[i])
            i += 1
        else:
            ltemp.append(li[j])
            j += 1
    while i<=mid:
        ltemp.append(li[i])
        i += 1
    while j <= high:
        ltemp.append(li[j])
        j+=1

    li[low:high+1] = ltemp

def mergesort(li,low,high):
    if low<high:
        mid = (low+high)//2
        mergesort(li,low,mid)
        mergesort(li,mid+1,high)
        merge(li,low,mid,high)

data = list(range(1000))
random.shuffle(data)
print(data)
mergesort(data,0,len(data)-1)
print(data)

希尔排序

希尔排序是插入排序的一种又称“缩小增量排序”，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

希尔排序的核心是对步长的理解，步长是进行相对比较的两个元素之间的距离，随着步长的减小，相对元素的大小会逐步区分出来并向两端聚拢，当步长为1的时候，就完成最后一次比较，那么序列顺序就出来了。

def shell_sort(alist):
    n = len(alist)
    gap = n // 2
    while gap >= 1:
        for j in range(gap, n):
            i = j
            while (i - gap) >= 0:
                if alist[i] < alist[i - gap]:
                    alist[i], alist[i - gap] = alist[i - gap], alist[i]
                    i -= gap
                else:
                    break
        gap //= 2


if __name__ == '__main__':
    li = [6, 5, 8, 45, 46, 98]
    shell_sort(li)
    print(li)

 堆排序

def sift(data, low, high):
    i = low
    j = 2 * i + 1
    tmp = data[i]
    while j <= high:
        if j < high and data[j] < data[j + 1]:
            j += 1
        if tmp < data[j]:
            data[i] = data[j]
            i = j
            j = 2 * i + 1
        else:
            break
    data[i] = tmp

def heap_sort(data):
    n = len(data)
    for i in range(n // 2 - 1, -1, -1):
        sift(data, i, n - 1)
    for i in range(n - 1, -1, -1):
        data[0], data[i] = data[i], data[0]
        sift(data, 0, i - 1)

if __name__ == '__main__':
    li = [6, 5, 8, 45, 46, 98]
    heap_sort(li)
    print(li)

堆排序应用1——top K

 

 

def sift(data, low, high):
    i = low
    j = 2 * i + 1
    tmp = data[i]
    while j <= high:
        if j < high and data[j] < data[j + 1]:
            j += 1
        if tmp < data[j]:
            data[i] = data[j]
            i = j
            j = 2 * i + 1
        else:
            break
    data[i] = tmp
def topn(li, n):
    heap = li[0:n]
    for i in range(n // 2 - 1, -1, -1):
        sift(heap, i, n - 1)  # 遍历
    for i in range(n, len(li)):
        if li[i] > heap[0]:
            heap[0] = li[i]
            sift(heap, 0, n - 1)
    for i in range(n - 1, -1, -1):
        heap[0], heap[i] = heap[i], heap[0]
        sift(heap, 0, i - 1)

 

堆排序应用2——优先队列

import heapq
def heapsort(li):
    h = []
    for value in li:
        heapq.heappush(h, value)
    return [heapq.heappop(h) for i in range(len(h))]

 

heapq.nlargest(100, li)

 

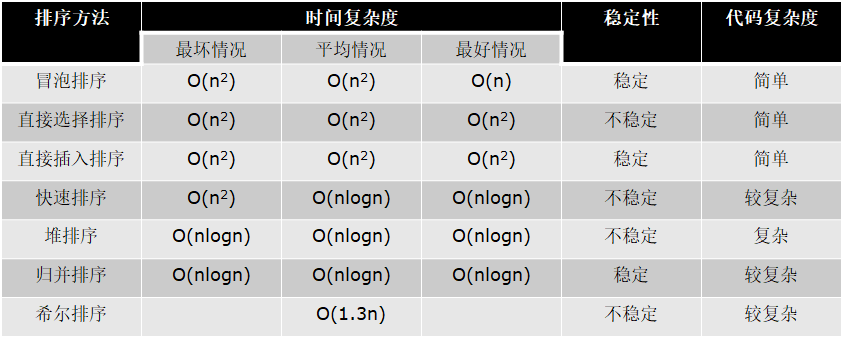
总结