数组

数组定义

格式1(推荐)：数据类型[] 变量名; 例： int[] arr;
格式2：数据类型 变量名[]; 例： int arr[];

初始化

就是为数组中的数组元素分配内存空间，并为每个数组元素赋值。数组的初始化分为两种方式：一种是静态初始化，一种是动态初始化。
静态初始化：初始化时指定每个数组元素的初始值，由系统决定数组长度
　　格式：数据类型[] 变量名 = new 数据类型[]{数据1,数据2,数据3,…};
　　　　例：int[] arr = new int[]{1,2,3};
　　简化格式：数据类型[] 变量名 = {数据1,数据2,数据3,…};
　　　　例：int[] arr = {1,2,3};

动态初始化：初始化时只指定数组长度，由系统为数组分配初始值
　　格式：数据类型[] 变量名 = new 数据类型[数组长度];
　　　　例：int[] arr = new int[3];
注意：两种初始化的方式是独立的，不可以混用。
获取数组长度(元素个数)：格式：数组名.length

数组内存图

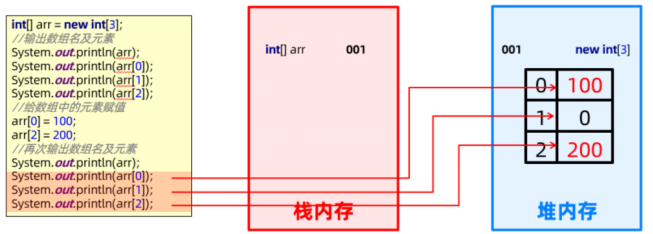
数组使用中经常遇到的两个小问题

1：索引越界（ArrayIndexOutOfBoundsException）：访问了数组中不存在的索引对应的元素，造成索引越界问题
2：空指针异常（NullPointerException）：对象不再指向堆内存，还想继续访问数据，访问失败

二维数组

格式1(推荐)：数据类型[] [] 变量名; 例： int[] [] arr;
格式2：数据类型 变量名[] []; 例： int arr[] [];
格式3：数据类型[] 变量名[]; 例： int[] arr[];

 二维数组初始化

静态初始化：
　　格式：数据类型[] [] 变量名 = new 数据类型[] []{{元素…},{元素…},{元素…},…};
　　　　例：int[] [] arr = new int[] []{{1,2,3},{4,5,6},{7,8,9}};
　　简化格式：数据类型[][] 变量名 = {{元素…},{元素…},{元素…},…};
　　　　例：int[] [] arr = {{1,2,3},{4,5,6},{7,8,9}};
　　注意：一维数组中元素的个位可以是不同的
　　　　如： int[] [] arr = new int[] []{{1,2,3},{4,5},{6,7,8,9}};
动态初始化：
　　格式：数据类型[] [] 变量名 = new 数据类型[m] [n];
　　　　例：int[] [] arr = new int[2] [3];

二维数组内存图

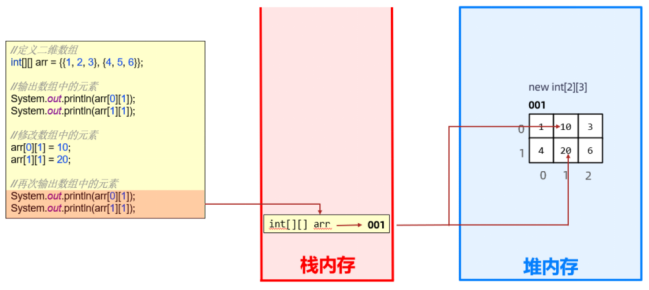
二维数组遍历及元素打乱

public class ArrayTest02 {
    public static void main(String[] args) {
        //定义二维数组，并进行静态初始化
        int[][] arr = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
        //创建随机数对象
        Random r = new Random();
        //遍历二维数组，进行元素打乱
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[i].length; j++) {
                //arr[i][j]
                int x = r.nextInt(arr.length);
                int y = r.nextInt(arr[x].length);
                //元素交换
                int temp = arr[i][j];
                arr[i][j] = arr[x][y];
                arr[x][y] = temp;
            }
        }
        //二维数组遍历展示
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr[i].length; j++) {
                System.out.print(arr[i][j] + " ");
            }
            System.out.println();
        }
    }
}

数组的高级操作

数组查找方法

一、顺序查找

　　顺序查找也叫线性查找，是最基本的一种查找方法。该算法是从给定的值中进行搜索，从一端开始逐一检查每个元素，直到找到所需的元素为止。在顺序查找中，元素序列的排列可以有序，也可以无序。查找时间较长。

二、二分查找

　　二分查找(Binary Search)算法，也叫折半查找算法。从一个序列中查找一个元素的时候，二分查找是一种非常快速的查找算法。二分查找是针对有序数据集合的查找算法，如果是无序数据集合就遍历查找。
　　二分查找之所以快速，是因为它在匹配不成功的时候，每次都能排除剩余元素中一半的元素。因此可能包含目标元素的有效范围就收缩得很快，而不像顺序查找那样，每次仅能排除一个元素。

原理：
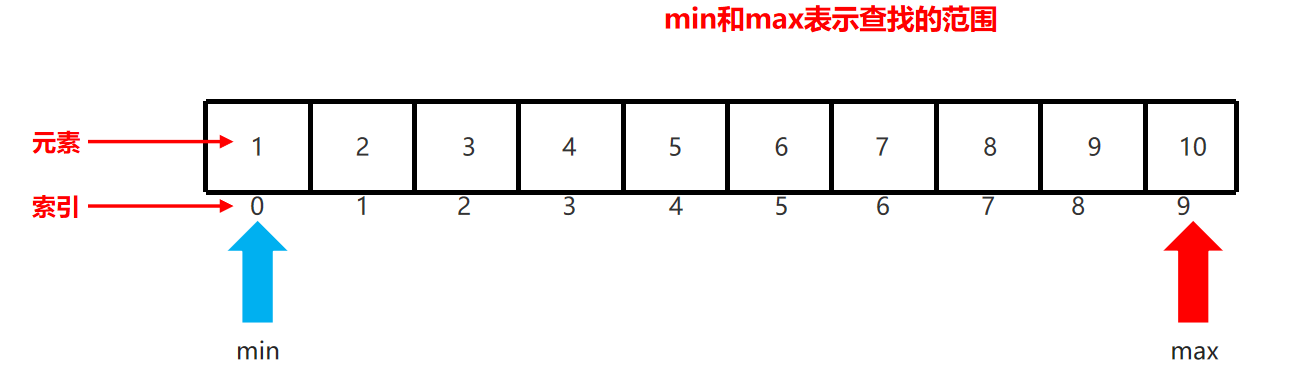
　　有一个有序表数组，按照从小到大的顺序来进行排列，需要在该有序表中查找元素3：

　　1、定义两个变量，表示要查找的范围。默认min = 0 ， max = 最大索引

　　　　

　　2、把整个数据集合长度分成两半，并用一个指针mid指向它们的临界点，mid=（min+max）/2，计算出mid的值（要求：min <= max）
　　3、判断mid位置的元素是否为要查找的元素

　　　　

　　4、如果要查找的值在mid的左半边，那么min值不变，max = mid-1.继续下次循环查找

　　　　

　　5、如果要查找的值在mid的右半边，那么max值不变，min = mid + 1.继续下次循环查找
　　6、如果mid位置的元素是要查找的元素，直接返回对应索引。

　　　　

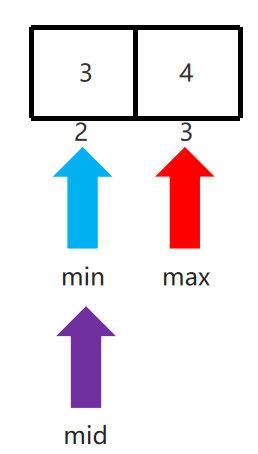
 　　7、当 min > max 时，表示要查找的元素在数组中不存在，返回-1.

代码实现：

public class MyBinarySearchDemo {
    public static void main(String[] args) {
        int [] arr = {1,2,3,4,5,6,7,8,9,10};
        int number = 11;

        int index = binarySearchForIndex(arr,number);
        System.out.println(index);
    }

    private static int binarySearchForIndex(int[] arr, int number) {
        //1,定义查找的范围
        int min = 0;
        int max = arr.length - 1;
        //2.循环查找 min <= max
        while(min <= max){
            //3.计算出中间位置 mid
            int mid = (min + max) >> 1;
            //mid指向的元素 > number
            if(arr[mid] > number){
                //表示要查找的元素在左边.
                max = mid -1;
            }else if(arr[mid] < number){
                //mid指向的元素 < number
                //表示要查找的元素在右边.
                min = mid + 1;
            }else{
                //mid指向的元素 == number
                return mid;
            }
        }
        //如果min大于了max就表示元素不存在,返回-1.
        return -1;
    }
}

优缺点：
　　优点：速度快，不占空间，不开辟新空间
　　缺点：必须是有序的数组，数据量太小没有意义

冒泡排序

相邻的数据两两比较，小的放前面，大的放后面。
如果有n个数据进行排序，总共需要比较n-1次
每一次比较完毕，下一次的比较就会少一个数据参与

原理：

1、相邻的元素两两比较，大的放右边，小的放左边，找到最大值。
2、第一次循环结束，最大值已经找到，在数组的最右边。

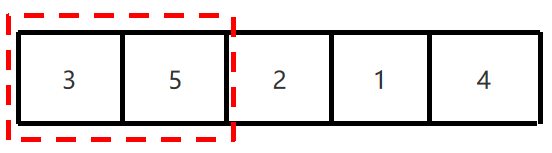
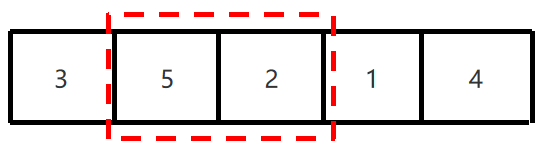
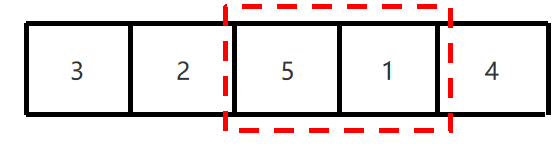
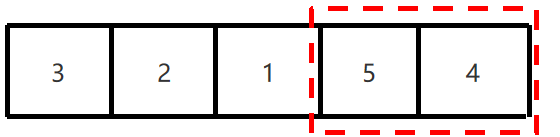
3、下一次只要在剩余的元素找最大值就可以了。
4、因为已经确定了5是最大值，所以4跟5无须再进行比较了。

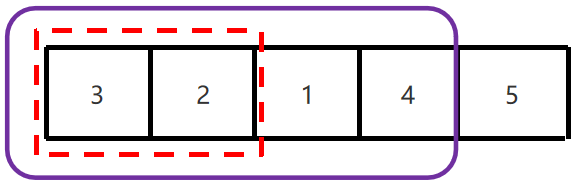
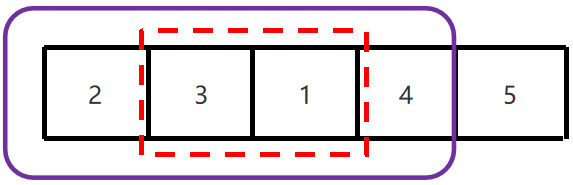
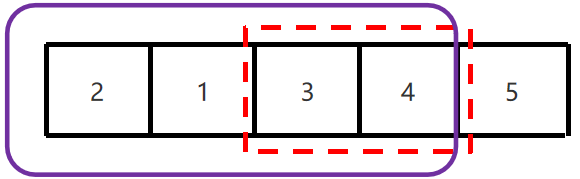
 5、按该规律依次比较，每一次比较完毕，下一次的比较就会少一个数据参与

代码实现：

public class MyBubbleSortDemo {
    public static void main(String[] args) {
        int[] arr = {3, 5, 2, 1, 4};
        //目标：{1 2 3 4 5}
        bubbleSort(arr);
    }

    private static void bubbleSort(int[] arr) {
        //外层循环控制的是次数 比数组的长度少一次.
        for (int i = 0; i < arr.length -1; i++) {
            //内存循环就是实际循环比较的
            //-1 是为了让数组不要越界
            //-i 每一轮结束之后,我们就会少比一个数字.
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
        printArr(arr);
    }

    private static void printArr(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }
}

递归

以编程的角度来看，递归指的是方法定义中调用方法本身的现象
递归解决问题的思路：
　　把一个复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解
　　递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算
递归解决问题要找到两个内容：
　　递归出口：否则会出现栈内存溢出异常（StackOverflowError）
　　递归规则：与原问题相似的规模较小的问题

代码实现：用递归求5的阶乘，并把结果在控制台输出

public class DiGuiDemo01 {
    public static void main(String[] args) {
        int result = jc(5);
        System.out.println("5的阶乘是："+ result);
    }

    public static int jc(int n) {
        //1.就是一定要找到出口.
        if(n == 1){
            return 1;
        }else{
            //2.就是递归的规则
            return n * jc(n - 1);
       }
    }
}

内存图：

　　

　　递归调用后弹栈消失

　　

　　输出结果