二视图从运动到结构----对极几何和基础矩阵
本文主要介绍对极几何和基础矩阵。
----------------------------------------------------
对极几何的出现时为了解决什么问题?
-----------------------------------------------------
从一张2D的图像估计3D模型有时十分困难(现在有基于深度学习的深度图估计,不清楚是否可以对这种场景3D还原)

这个时候,双/多 摄像头就可以帮助解决3D恢复的问题
立体视觉几何中有以下问题:
1.已知一幅图像中一点,如何寻找另一幅图像中这个点的对应点(根据是否知道相机的相对位置,此问题求解方式不同)
2.已知两幅图像中两点是对应关系,如何求解两相机的相对位置和姿态
3.已知多幅图像中同一3D点的对应点,如何求解该3D点的3D坐标
对极几何/基础矩阵 的出现可以解决问题2。
----------------------------------------------------
对极几何是什么?
-----------------------------------------------------
1.基本概念
立体成像的基本几何就是对极几何。下图是最经典的对极几何示意图。

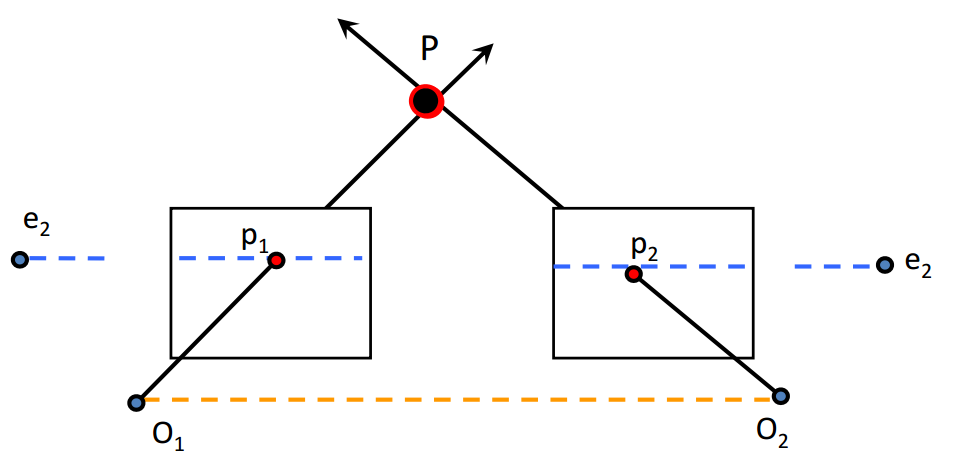
O1和O2为两个相机(也有可能是一个相机在不同时刻的位置)的主点,P为空间中一个物点,两个相对的白色平面是像面(严格按照光路应该是在O1 O2点的后方,与P点相反方向,CV中默认采用这种往前画的方式节省空间)。p1和p2是P点在像面上的对应点,e1 e2为像面和O1 O2的交点。O1O2为基线,也被称作相机的移动方向。
在对极几何中,e1和e2被称作极点,PO1O2平面为极面,p1e1为极线,同理p2e2也为极线。这是对极几何中重要的三个概念。
2. 极点性质
下面介绍极点的性质:
=像平面和的基线O1O2交点
=O2在相机1上的像点为e1
=基线的平行线在各自像面上的消失点
重点阐述一下第3个性质,
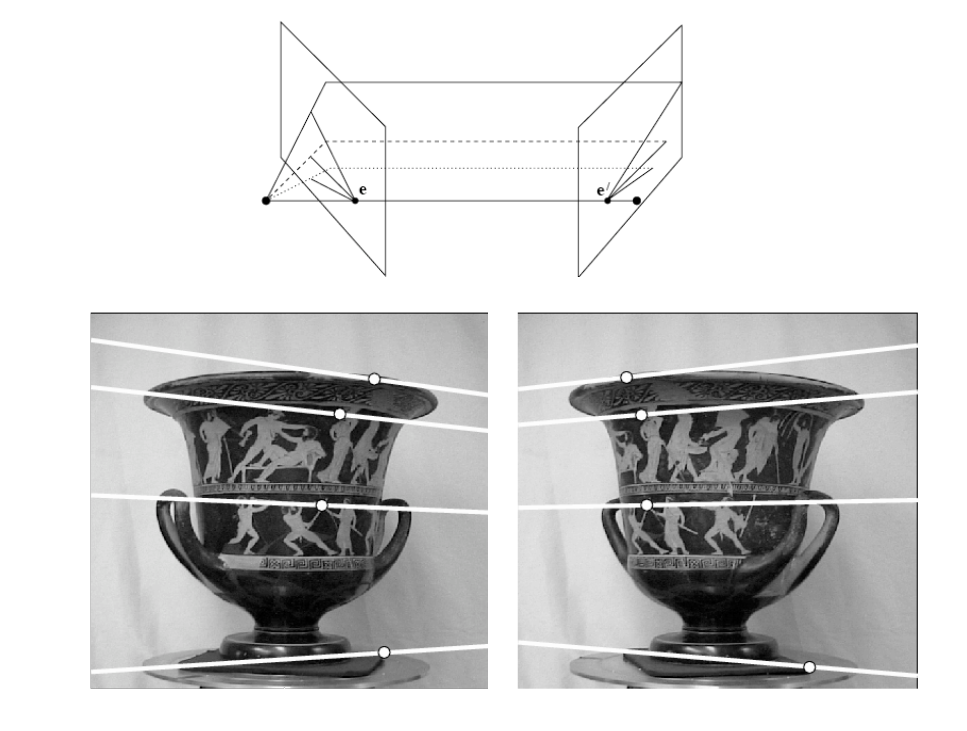
A. 如图,两个相机相对放置(会聚视角), 相机1面向右边,相机2面向左边,可知极点位于1的右边,2的左边。图中花瓶上标示的横线即为平行于基线的线条。
为什么平行于基线的线条消失点为极点?可以看上图,平行于基线的线条所在极面与像面必交于极点(基线必与像面交于极点),故而这些线条在像面上一定会交于极点。
B. 当两个像面平行时,根据极点的定义,则极点位于无穷远处,极线与基线平行, 如下图所示
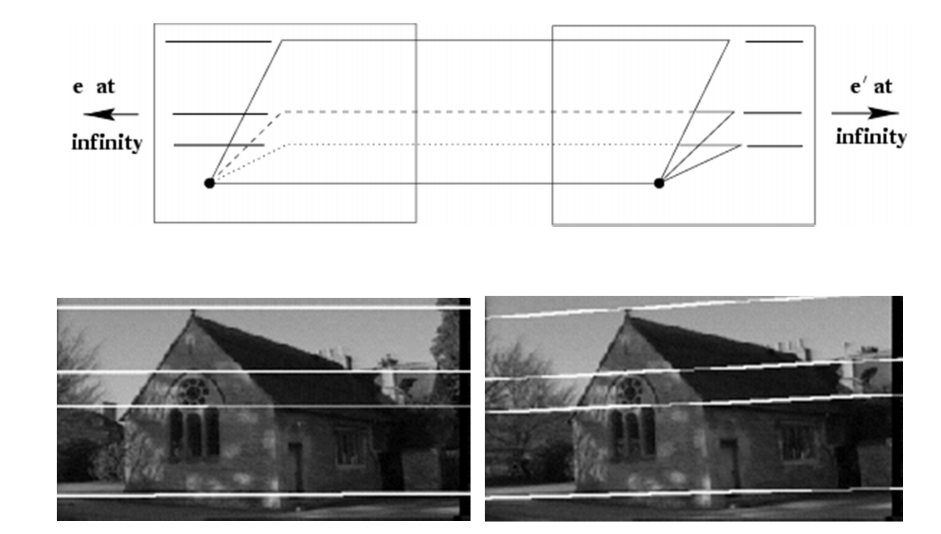
这个时候,与基线平行的线条的在像面是一系列平行线,消失点在无穷远,和极点重合
C. 当两个相机是前后放置且主点连线和像面垂直时(forward translation)
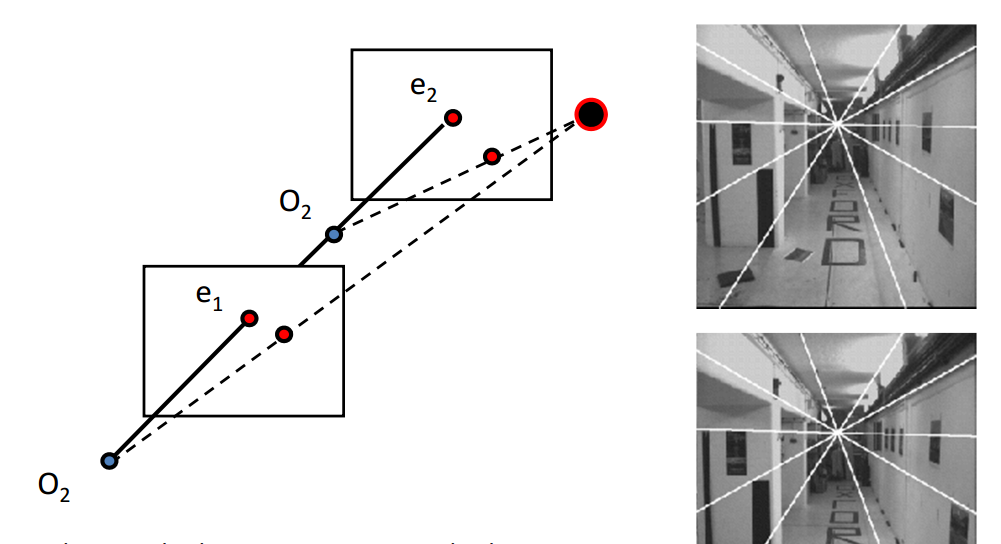
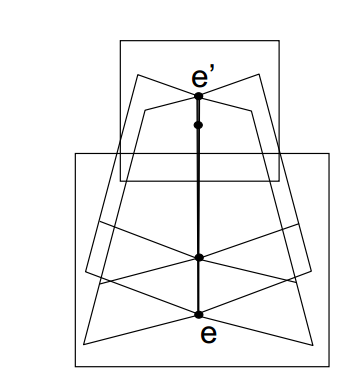
极点在各自像平面上的位置相同,且平行基线的线条在像面上的位置如上图右边所示。同样消失点为极点。
3.对极约束

p点在像面2上的对应点一定在极线l'上
--------------------------------------
基础矩阵是什么
--------------------------------------
如果已知基础矩阵F,以及一个3D点在一个像面上的像素坐标p,则可以求得在另一个像面上的像素坐标p'。这个是基础矩阵的作用,可以表征两个相机的相对位置及相机内参数。
下面具体介绍基础矩阵与像素坐标p和p'的关系。重点来了~
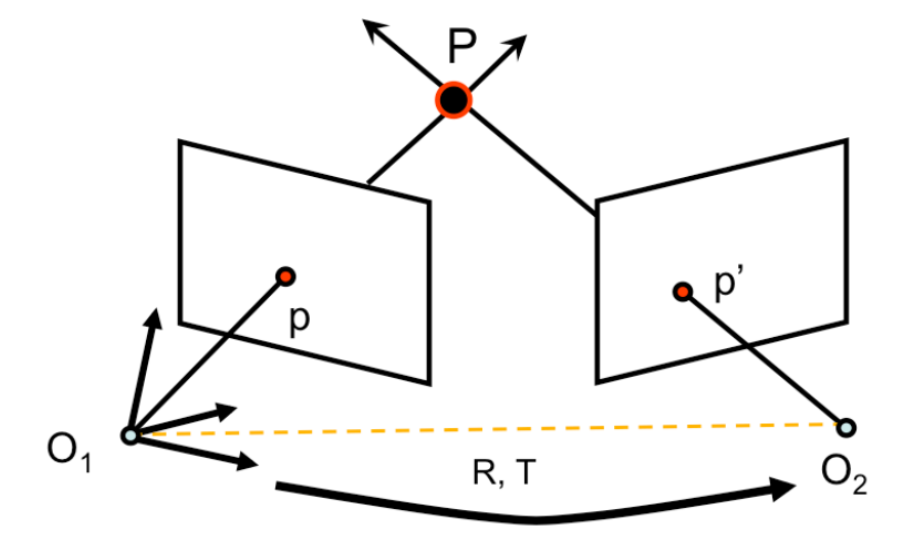
以O1为原点,光轴方向为z轴,另外两个方向为x, y轴可以得到一个坐标系,在这个坐标系下,可以对P, p1(即图中所标p), p2(即图中所标p')得到三维坐标,同理,对O2也可以得到一个三维坐标,这两个坐标之间的转换矩阵为[R T],即通过旋转R和平移T可以将O1坐标系下的点P1(x1, y1, z1), 转换成O2坐标系下的P2(x2, y2, z2)。
则可知,P2 = R(P1-T) (1)
采用简单的立体几何知识,可以知道
![]() (2)
(2)
其中,p, p'分别为P点的像点在两个坐标系下分别得到的坐标(非二维像素坐标)。Rp'为极面上一矢量,T为极面上一矢量,则两矢量一叉乘为极面的法向量, 这个法向量与极面上一矢量p一定是垂直的,所以上式一定成立。(这里采用转置是因为p会表示为列向量的形式,此处需要为行向量)
采用一个常用的叉乘转矩阵的方法,
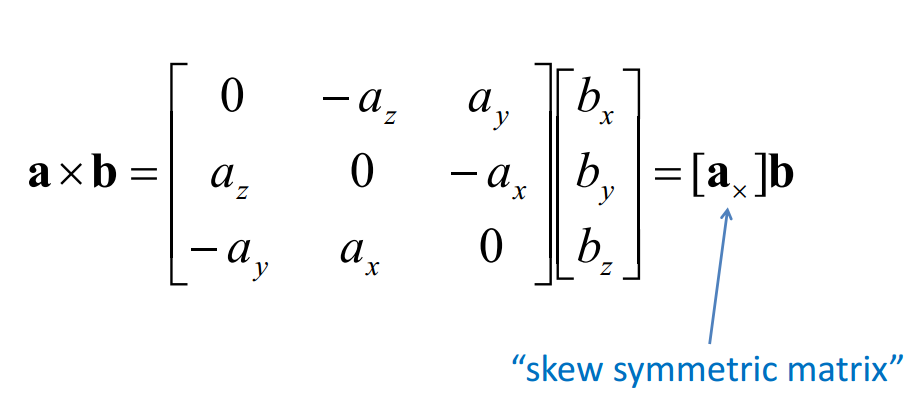 (3)
(3)
将我们的叉乘采用上面的转换,会变成
![]() (4)
(4)
红框中所标即为本征矩阵E, 他描述了三维像点p和p'之间的关系
![]() (5)
(5)
有了本征矩阵,我们的基础矩阵也就容易推导了
注意到将p和p'换成P1和P2式(4)也是成立的,且有
q1 = K1P1 (6)
q2 = K2P2 (7)
上式中, K1K2为相机的校准矩阵, 描述相机的内参数 q1q2为相机的像素坐标
代入式(4)中,得
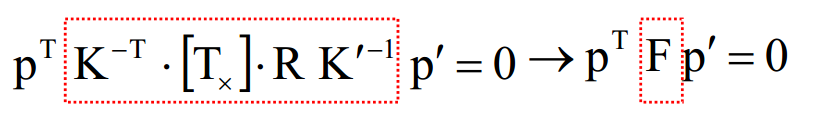 (8)
(8)
上式中p->q1, p'->q2
这样我们就得到了两个相机上的像素坐标和基础矩阵F之间的关系了
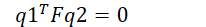 (9)
(9)
-------------------------------------
基础矩阵的性质
-------------------------------------
F有什么样的性质呢?简单说来, 3x3的矩阵,理论上9个自由度,但是需要符合以下两个约束
a)如果F为基础矩阵,那么kF也为基础矩阵
b)秩为2
所以减去两个自由度,F有7个自由度
第二条约束是怎么来的?
我们知道,矩阵的秩有这么一个性质,矩阵相乘的秩不大于各矩阵的秩
那么,可以知道F其实是以下这些矩阵相乘的结果
![]()
其中,Tx的具体形式在式(3)中有表述
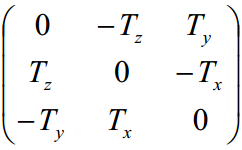
可以知道,第三列A2可以用第一列A0和第二列A1线性表示
A2 = -Ty*A1/Tz-Tx*A0/Tz
所以Tx秩为2
那么F秩为2也得证了
一般采用七点算法或八点算法对F进行求解,得知F后就可以对任意像面1上点找像面2上对应点了。
Reference:
1. Computer vision algo and application
2. learning openCV
3. multiple view geometry in computer vision
4. CV slides of Li Feifei



