guided filter总结

 输入有两张图，引导图I和输入的图p，输出的图为q。

在我们的matting的例子里面，引导图是原图或者是原图的灰度图，输入p为粗粗的分割后的结果， 输出q是具有精细边缘的matting图。

 

I和输出q之间需要满足一个关系，在任意一个半径为r的窗口内，满足q和I之间是线性的，ak和bk在窗口wk内是常数。

 

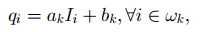
这个设想是合理的，在边界的地方，是想要服从这个的。但是在背景和前景区域，实际上并不想要符合这个，可以看鸭子的脖子和身体之间蓝黄色的交界处，实际上并不想要这个梯度的，所以需要引入下一个约束

 

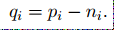
要让q和p之间的对应像素间差值尽可能的小，这样在大块的前景和背景区域，就都还是原来的值了。在这种窗口wk内如果输入p都是背景(p=0)的话，那么直接ak=0,bk=0,就可以得到q=0，整个窗口q还是背景。如果p=255，那么ak=0,bk = 255，整个窗口q是前景255。

这都比较好理解，那么在窗口既有背景又有前景的时候（就是边界），就需要保留I中的像素梯度关系了，这样就需要去求这个窗口wk中的ak和bk，求解也比较简单，就是在这个半径为r的窗口寻找一个ak和一个bk满足以下方程最小，ƹ是正则项。

 

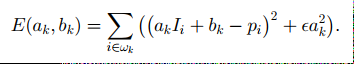
线性回归，得到

 

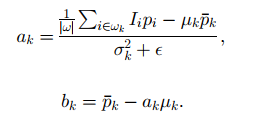
这样就可以求到ak,然后每一个点在实际算的时候，被很多个窗口包围，每个窗口都可以算出一个a和b来，如下图qi这个点被3个窗口包含，实际上比这个还要多。

 

所以在算的时候会把所有点在这里的a和b去求一个平均，求了平均值后语义就跟之前有一些不一样了，q和I就不是成线性的关系了，但是因为a和b都是平均后的值，梯度非常小，所以在I上有大梯度的时候，仍然可以看做I的梯度和q的梯度是线性的，如下图，后面两项可以忽略不计。

 

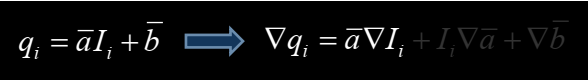
整个算法的流程如下

 

可以看到，主要是一个boxfilter，即半径为r的窗口内求所有像素的平均

采用积分图，让这个运算的复杂度和r的大小无关，那么这个是算法就是O(N)的，N是图像的像素数，只与分辨率有关。

为了加速这个引导滤波，作者提出来可以在小分辨率上计算a和b然后upscale到大分辨率再和I取计算q。这种方法可能会损失一部分非常小的细节，大部分的是可以保留的。

 ------------------------------------------------------------------------------------------------------------------

Guided filter现在有一个trainable的版本，意思是可以和前面的cnn网络一起训练，不仅仅是一个后处理的模块，这样end-to-end的训练会让结果更好。论文主要是论证了guided Filter的反向传播是可微的。

论文在这里 https://arxiv.org/pdf/1803.05619v1.pdf

 

具体推导是这样的

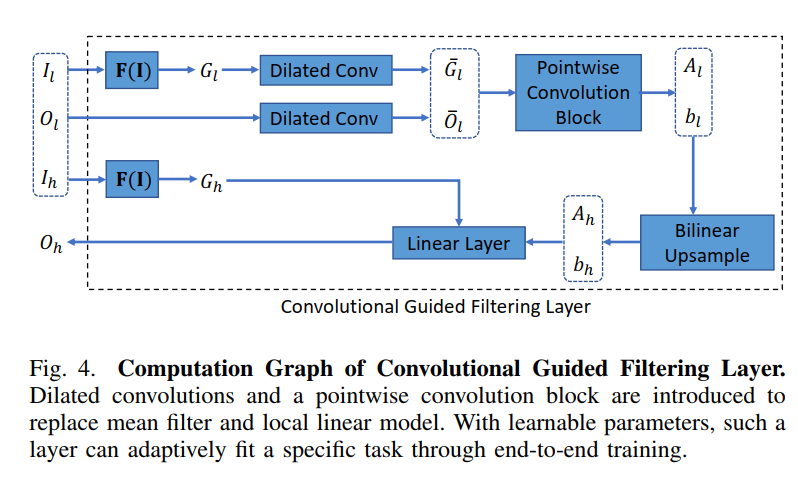
这个是guided filter的流程图

 

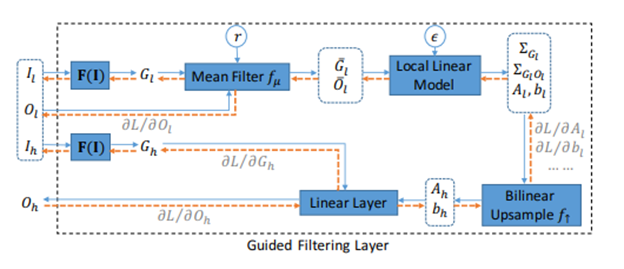
有三个输入，Il是小分辨率的RGB图像，Ol是经过网络后初步的mask，也是小分辨率的。根据Il和Ol去计算出小分辨率上面的ak和bk然后upscale，再对输入的大分辨率的Ih去做计算，得到大分辨率的Oh,这里需要注意的是，Il对应的是I,Ol对应的是p，Ih对应的是I，Oh对应的是q。所以Ol和Oh长的像但是不是一个意思。

仿照guided filter的求解过程，计算Al和Bl。这里先暂时忽略F(I)， 这个是作者自己提出来的做guided map的几层卷积，可忽略。那么有以下的推导过程

 

简单的，如果去计算

反向传播的时候，需要计算

然后就可以一步一步推导下去，直到推导出

具体过程如下图所示，其中的

 

可以看到确实是可反向求导的。

 

这篇文章有source code可以看看具体是怎么用pytorch code实现guided fitler的

 def forward(self, lr_x, lr_y, hr_x):
        n_lrx, c_lrx, h_lrx, w_lrx = lr_x.size()
        n_lry, c_lry, h_lry, w_lry = lr_y.size()
        n_hrx, c_hrx, h_hrx, w_hrx = hr_x.size()

        assert n_lrx == n_lry and n_lry == n_hrx
        assert c_lrx == c_hrx and (c_lrx == 1 or c_lrx == c_lry)
        assert h_lrx == h_lry and w_lrx == w_lry
        assert h_lrx > 2*self.r+1 and w_lrx > 2*self.r+1

        ## N
        N = self.boxfilter(Variable(lr_x.data.new().resize_((1, 1, h_lrx, w_lrx)).fill_(1.0)))

        ## mean_x
        mean_x = self.boxfilter(lr_x) / N
        ## mean_y
        mean_y = self.boxfilter(lr_y) / N
        ## cov_xy
        cov_xy = self.boxfilter(lr_x * lr_y) / N - mean_x * mean_y
        ## var_x
        var_x = self.boxfilter(lr_x * lr_x) / N - mean_x * mean_x

        ## A
        A = cov_xy / (var_x + self.eps)
        ## b
        b = mean_y - A * mean_x

        ## mean_A; mean_b
        mean_A = F.interpolate(A, (h_hrx, w_hrx), mode='bilinear', align_corners=True)
        mean_b = F.interpolate(b, (h_hrx, w_hrx), mode='bilinear', align_corners=True)

        return mean_A*hr_x+mean_b

 看起来也还是可以的。

文章后面又提出了conv guided filter，用卷积去做的几层， 其中dilated conv的rate就是radius，感觉可解释性下降了。下面是conv guided filter的具体思想。