算法(一)
public static void main(String[] args) {
System.out.println(1<<35);
System.out.println(1<<3);
}
输出的结果都是:8
1.十进制转二进制
原理:给定的数循环除以2,直到商为0或者1为止。将每一步除的结果的余数记录下来,然后反过来就得到相应的二进制了。
比如8转二进制,第一次除以2等于4(余数0),第二次除以2等于2(余数0),第三次除以2等于1(余数0),最后余数1,得到的余数依次是0 0 0 1 ,
反过来就是1000,计算机内部表示数的字节长度是固定的,比如8位,16位,32位。所以在高位补齐,java中字节码是8位的,所以高位补齐就是00001000.
所以(8)10=(00001000)2;
2.二进制转十进制
比如8的二进制表示位00001000,去掉补齐的高位就是1000.从个位开始计算2的幂,(个位是0,依次往后推)乘以对应位数上的数,然后得到的值相加
(2的0次幂)*0+(2的1次幂)*0+(2的2次幂)*0+(2的3次幂)*1 = 8
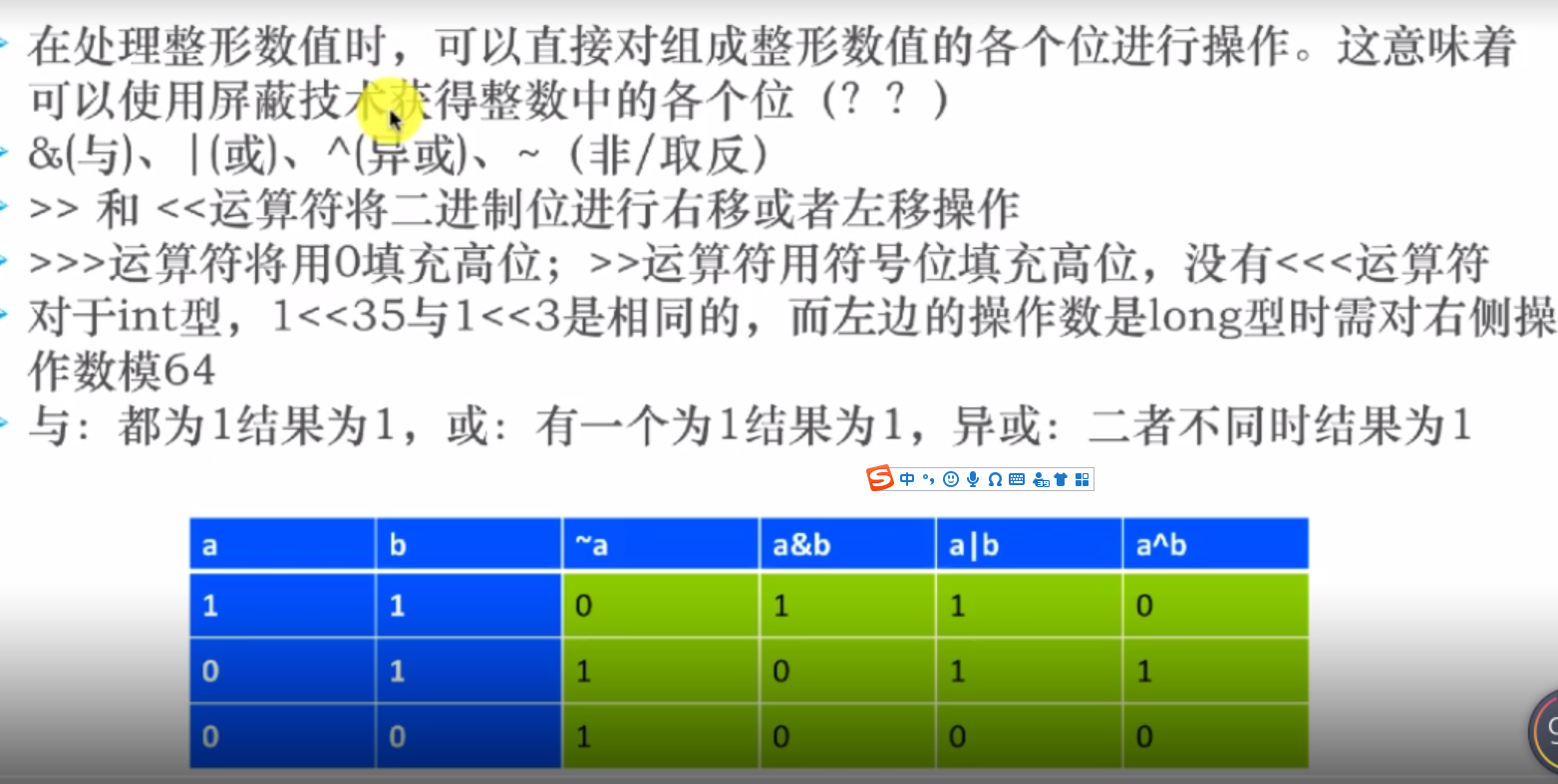
3.位异或运算(^)
运算规则是:两个数转为二进制,然后从高位开始比较,如果相同则为0,不相同则为1。
比如:8^11.
8转为二进制是1000,11转为二进制是1011.从高位开始比较得到的是:0011.然后二进制转为十进制,就是3
4.位与运算符(&)
运算规则:两个数都转为二进制,然后从高位开始比较,如果两个数都为1则为1,否则为0
比如:129&128.
129转换成二进制就是10000001,128转换成二进制就是10000000。从高位开始比较得到,得到10000000,即128.
5.位或运算符(|)
比如:129|128.
129转换成二进制就是10000001,128转换成二进制就是10000000。从高位开始比较得到,得到10000001,即129.
6.位非运算符(~)
运算规则:如果位为0,结果是1,如果位为1,结果是0.
在Java中,所有数据的表示方法都是以补码的形式表示,如果没有特殊说明,Java中的数据类型默认是int,int数据类型的长度是8位,一位是四个字节,就是32字节,32bit.
8转为二进制是100101.
补码后为: 00000000 00000000 00000000 00100101
取反为: 11111111 11111111 11111111 11011010
因为高位是1,所以原码为负数,负数的补码是其绝对值的原码取反,末尾再加1。
因此,我们可将这个二进制数的补码进行还原: 首先,末尾减1得反码:11111111 11111111 11111111 11011001 其次,将各位取反得原码:
00000000 00000000 00000000 00100110,此时二进制转原码为38
所以~37 = -38.
三种移位运算符:
<< : 左移运算符,不分正负数,低位补0;相当于乘以2
>> : 如果该数为正,则高位补0,若为负数,则高位补1;相当于除以2
>>> : 表示无符号右移,也叫逻辑右移,即若该数为正,则高位补0,而若该数为负数,则右移后高位同样补0
/**
* 【如何找到数组中唯一成对的那个数?】
* 1-1000这个1000个数放在含有1001个元素的数组中,
* 只有唯一的一个元素值重复,其它均只出现一次。
* 每个数组元素只能访问一次,
* 设计一个算法,将它找出来;不用辅助空间。
*/
import java.util.HashSet;
import java.util.Random;
import utils.Utils;
public class 唯一成对的数 {
public static void main(String[] args) {
//首先生成一个1-N的数组,有一个数重复
int N=11;
int[] arr=new int[N];
for(int i=0;i<arr.length-1;i++){
arr[i]=i+1;
}
//最后一个数是随机数
arr[arr.length-1]=new Random().nextInt(N-1)+1;
//随机下标
int index=new Random().nextInt(N);
Utils.swap(arr,index,arr.length-1);
Utils.print(arr);
int result = 0;
//方法一: 异或运算符 a^a=0, a^0=a
for(int i=1;i<=N-1;i++){
result=(result^i);
}
for(int i=0;i<N;i++){
result = result^arr[i];
}
System.out.println(result);
//1.2
int result1 = 0;
// 异或运算符 a^a=0, a^0=a
for(int i = 1; i < arr.length; i++) {
result1 = i^result1;
}
for(int i = 0; i < arr.length; i++) {
result1 = result1^arr[i];
}
System.out.println(result1);
System.out.println("================");
//方法二
int[] helper=new int[N];
for(int i=0;i<N;i++){
helper[arr[i]]++;
}
for(int i=0;i<N;i++){
if(helper[i]==2){
System.out.println(i);
break;
}
}
//方法三
HashSet<Integer> set=new HashSet<Integer>();
for(int i=0;i<arr.length;i++){
if(set.add(arr[i])!=true){
System.out.println(arr[i]);
return;
}
}
}
}
C#版本:
static void Main(string[] args)
{
//Console.WriteLine("Hello World!");
int num = 11;
int[] arr = new int[num];
for (int i = 0; i < arr.Length - 1; i++)
arr[i] = i + 1;
//最后一个数是随机数
arr[arr.Length - 1] = new Random().Next(num - 1) + 1;
//随机下标
int index = new Random().Next(num);
Swap(arr, index, arr.Length - 1);
Print(arr);
int result = 0;
//方法一1.1: 异或运算符 a^a=0, a^0=a
for (int i = 1; i < arr.Length; i++)
result = i ^ result;
for (int i = 0; i < arr.Length; i++)
result = result ^ arr[i];
Console.WriteLine(result);
//1.2
int result2 = 0;
for (int i = 1; i <= num - 1; i++)
result2 = result2 ^ i;
for (int i = 0; i < num; i++)
result2 = result2 ^ arr[i];
Console.WriteLine(result2);
//方法二
int[] helper = new int[num];
for (int i = 0; i < num; i++)
helper[arr[i]]++;
for (int i = 0; i < num; i++)
{
if (helper[i] == 2)
{
Console.WriteLine(i);
break;
}
}
//方法三
HashSet<int> set = new HashSet<int>();
for (int i = 0; i < arr.Length; i++)
{
if (set.Add(arr[i]) != true)
{
Console.WriteLine(arr[i]);
return;
}
}
}
public static void Swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void Print(int[] arr)
{
Console.WriteLine("[");
for (int i = 0; i < arr.Length; i++)
Console.WriteLine(arr[i]+",");
Console.WriteLine(arr[arr.Length-1]+"]");
}
/**
* 【二进制中1的个数】 请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。 例:9的二进制表示为10001,有2个是1
*/
public class CountBinary {
/**
* 【二进制中1的个数】 请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。 例:9的二进制表示为10001,有2位是1
*/
public static void main(String[] args) {
int n = 2000;
System.out.println(Integer.toBinaryString(n));
int count = funcition1(n);
System.out.println(count);
count = function2(n);
System.out.println(count);
count = function3(n);
System.out.println(count);
count =function4(n);
System.out.println(count);
}
private static int funcition1(int n) {
int count = 0;
while(n != 0) {
if((n & 1) == 1){
count++;
}
n = n >> 1;
}
return count;
}
//方法二
public static int function2(int n){
int count = 0;
for (int i = 0; i < 32; i++) {
if((n&(1<<i))==(1<<i)){
count++;
}
}
return count;
}
//方法三
public static int function3(int n){
int count = 0;
while(n != 0){
n = (n-1)&n;
count++;
}
return count;
}
private static int function4(int n){
int count=0;
for(int i=0;i<32;i++){
if(((n>>>i)&1)==1)
count++;
}
return count;
}
}



