JAVA二分搜索树
二叉树:
和链表一样,动态数据结构。
二叉树具有唯一根节点
二叉树具有天然的递归结构
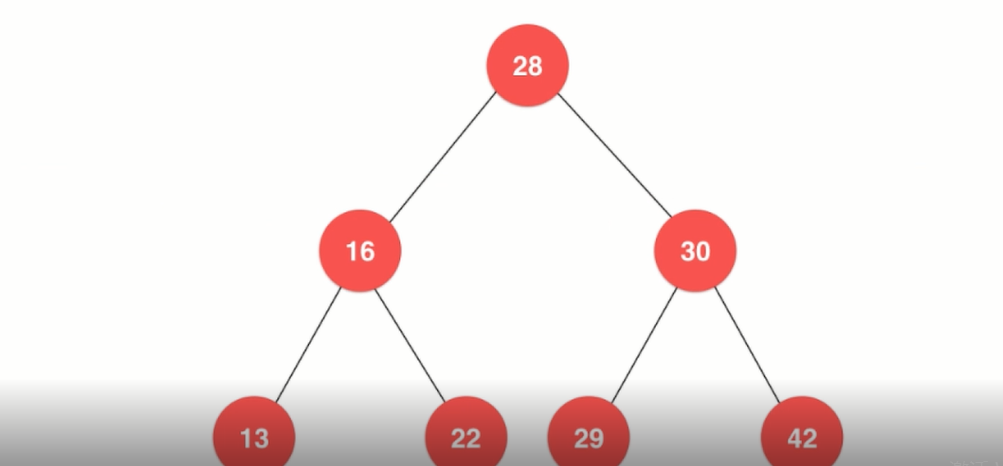
二分搜索树是二叉树
二分搜索树的每个节点的值:
1.大于其左子树的所有节点的值
2.小于其右子树的所有节点的值
每一颗子数也是二分搜索树
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 | public class BST<E extends Comparable<E>> { private class Node{ public E e; public Node left,right; public Node(E e){ this.e=e; left=null; right=null; } } private Node root; private int size; public BST(){ root=null; size=0; } public int size(){ return size; } public boolean isEmpty(){ return size==0; } public void add(E e){ if(root==null){ root=new Node(e); size++; }else{ add(root,e); } } 向以Node为跟节点的二分搜索树中插入元素E递归算法 private void add(Node node,E e){ if(e.equals(node.e)) return ; else if(e.compareTo(node.e)<0&&node.left==null){ node.left=new Node(e); size++; return ; }else if(e.compareTo(node.e)>0&&node.right==null){ node.right=new Node(e); size++; return; } if(e.compareTo(node.e)<0) add(node.left,e); else add(node.right, e);public void add(E e){ root=add(root, e); } private Node add(Node node,E e){ if(node==null){ size++; return new Node(e); } if(e.compareTo(node.e)<0) node.left=add(node.left, e); else if(e.compareTo(node.e)>0) node.right=add(node.right, e); return node; } //看二分搜索树中是否包含元素e public boolean contains(E e){ return contains(root,e) } //以node为根的二分搜索树中是否包含元素e,递归算法 public boolean contains(Node node,E e){ if(node==null) return false; if(e.compareTo(node.e)==0) return true; else if(e.compareTo(node.e)<0) return contains(node.left,e); else return contains(node.right, e); }} |
二分搜索树的前序遍历:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | //二分搜索树的前序遍历 public void preOrder(){ preOrder(root); } //前序遍历以node为根的二分搜索树,递归算法 private void preOrder(Node node){ if(node==null) return; System.out.println(node.e); preOrder(node.left); preOrder(node.right); } @Override public String toString(){ StringBuilder res=new StringBuilder(); generateBSTString(root,0,res); return res.toString(); } //生成node为根节点,深度为depth的描述二叉树的字符串 private void generateBSTString(Node node,int dept,StringBuilder res){ if(node==null){ res.append(generateDepthString(dept)+"null\n"); return; } res.append(generateDepthString(dept)+node.e+"\n"); generateBSTString(node.left,dept+1,res); generateBSTString(node.right,dept+1,res); } private String generateDepthString(int dept) { StringBuilder res=new StringBuilder(); for(int i=0;i<dept;i++) res.append("--"); return res.toString(); } |
测试:
1 2 3 4 5 6 7 8 9 10 11 | public class Main { public static void main(String[] args){ BST<Integer> bst=new BST<>(); int[] nums={5,3,6,8,4,2}; for(int num:nums) bst.add(num); bst.preOrder(); System.out.println(); System.out.println(bst); } } |
二分搜索树的中序遍历和后续遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | //二分搜索树的中序遍历 public void inOrder(){ inOrder(root); } //中序遍历以node为根的二分搜索树,递归算法 private void inOrder(Node node){ if(node==null) return ; inOrder(node.left); System.out.println(node.e); inOrder(node.right); } //二分搜索树的后续遍历 public void postOrder(){ postOrder(root); } //后续遍历以node为根的二分搜索树,递归算法 private void postOrder(Node node){ if(node==null) return ; postOrder(node.left); postOrder(node.right); System.out.println(node.e); } |
测试:
1 2 3 4 5 6 | bst.preOrder(); System.out.println(); bst.inOrder(); System.out.println(); bst.postOrder(); System.out.println(); |
1 2 3 4 5 6 7 8 9 10 11 12 13 | //二分搜索树的非递归前序遍历 public void preOrderNR(){ Stack<Node> stack=new Stack<>(); stack.push(root); while (!stack.isEmpty()) { Node cur=stack.pop(); System.out.println(cur.e); if(cur.right!=null) stack.push(cur.right); if(cur.left!=null) stack.push(cur.left); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 | //二分搜索树的层序遍历public void levelOrder(){ Queue<Node> queue=new LinkedList<>(); queue.add(root); while (!queue.isEmpty()) { Node cur=queue.remove(); System.out.println(cur.e); if(cur.left!=null) queue.add(cur.left); if(cur.right!=null) queue.add(cur.right); }} |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | //寻找二分搜索树的最小元素 public E mininum(){ if(size==0) throw new IllegalArgumentException("BST is empty"); return mininum(root).e; } //返回以node为根的二分搜索树的最小值所在的节点 private Node mininum(Node node){ if(node.left==null) return node; return mininum(node.left); } //寻找二分搜索树的最大元素 public E maximum(){ if(size==0) throw new IllegalArgumentException("BST is empty"); return maximum(root).e; } //返回node为根的二分搜索树的最大值所在的节点 private Node maximum(Node node){ if(node.right==null) return node; return maximum(node.right); } //从二分搜索树中删除最小值所在节点,并返回最小值 public E removeMin(){ E ret=mininum(); root=removeMin(root); return ret; } //删除掉以node为根的二分搜索树中的最小节点 //返回删除节点后新的二分搜索树的根 private Node removeMin(Node node){ if(node.left==null){ Node rightNode=node.right; node.right=null; size--; return rightNode; } node.left= removeMin(node.left); return node; } //从二分搜索树中删除最大值所在节点 public E removeMax(){ E ret=maximum(); root=removeMax(root); return ret; } //删除掉以node为根的二分搜索树中的最大节点 //返回删除节点后新的二分搜索树的根 public Node removeMax(Node node){ if(node.right==null){ Node leftNode=node.left; node.left=null; size--; return leftNode; } node.right=removeMax(node.right); return node; } |
测试
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | public class Main { public static void main(String[] args){ BST<Integer> bst=new BST<>(); Random random=new Random(); int n=1000; for(int i=0;i<n;i++) bst.add(random.nextInt(10000)); ArrayList<Integer> nums=new ArrayList<>(); while(!bst.isEmpty()) nums.add(bst.removeMin()); System.out.println(nums); for(int i=1;i<nums.size();i++) if(nums.get(i-1)>nums.get(i)) throw new IllegalArgumentException("Error"); System.out.println("removeMin test completed."); //test removeMax for(int i=0;i<n;i++) bst.add(random.nextInt(10000)); nums=new ArrayList<>(); while(!bst.isEmpty()) nums.add(bst.removeMax()); System.out.println(nums); for(int i=1;i<nums.size();i++) if(nums.get(i-1)<nums.get(i)) throw new IllegalArgumentException("Error"); System.out.println("removeMax test completed."); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | //从二分搜索树中删除元素为e的节点 public void remove(E e){ root=remove(root,e); } //删除以node为根的二分搜索树中值为e的节点,递归算法 //返回删除节点后新的二分搜索树的根 private Node remove(Node node,E e){ if(node==null) return null; if(e.compareTo(node.e)<0){ node.left=remove(node.left, e); return node; } else if(e.compareTo(node.e)>0){ node.right= remove(node.right, e); return node; }else { //待删除节点左子树为空的情况 if(node.left==null){ Node rightNode=node.right; node.right=null; size--; return rightNode; } //待删除节点右子数为空的情况 if(node.right==null){ Node leftNode=node.left; node.left=null; size--; return leftNode; } //待删除节点左右子数均不为空的情况 //找到比待删除节点大的最小节点,即待删除节点右子树的最小节点 //用这个节点顶替待删除节点的位置 Node successor=mininum(node.right); successor.right=removeMin(node.right); successor.left=node.left; node.left=node.right=null; return successor; } } |




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 用 C# 插值字符串处理器写一个 sscanf
· Java 中堆内存和栈内存上的数据分布和特点
· 开发中对象命名的一点思考
· .NET Core内存结构体系(Windows环境)底层原理浅谈
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· DeepSeek 解答了困扰我五年的技术问题。时代确实变了!
· 本地部署DeepSeek后,没有好看的交互界面怎么行!
· 趁着过年的时候手搓了一个低代码框架
· 推荐一个DeepSeek 大模型的免费 API 项目!兼容OpenAI接口!
2018-03-25 SQL Server索引维护