CF VP

• \(\color{green}\checkmark\)：vp 时场切。
• \(\color{red}(\checkmark)\)：赛后自己切掉。
• \(\color{red}\times\)：看题解才会。

CF1446

A. Knapsack \(\color{green}{\checkmark}\)

唐氏贪心题。

B. Catching Cheaters \(\color{green}{\checkmark}\)

考虑 dp。设 \(f_{x,y}\) 表示 \(s\) 考虑 \(x\) 位，\(t\) 考虑 \(y\) 位的答案，转移：

\(f_{x,y} = \begin{cases}f_{x-1,y-1}+2 \; (s_x = t_y)\\\max(0,\max(f_{x-1,y},f_{x,y-1}-1)) \; (s_x \ne t_y)\end{cases}\)

然后幽默的是 vp 时没和 \(0\) 取 \(\max\) 狂吃 2 发罚时。

C. Xor Tree \(\color{red}{\times}\)

不会转化条件，没救了。

结论：基环树上环长不会超过 \(2\)。

考虑建出 01trie，对于 \((i,j)\) 这一条边，找到第一个不同的二进制位 \(b\)。考虑 \(j\) 号点的连边，设其连边为 \((j,k)\)。

• 如果 \(j,k\) 的第一个不同二进制位也是 \(b\)，则 \(k = i\)。
• 否则，\(k\) 的连边一定在 \(b'\) 的子树内，不可能是 \(i\)。

因此，设 \(f_x\) 表示 \(x\) 子树内最多保留的点，如果它有两个儿子，那么保留大的那个子树，另一个子树最多保留一个。容易转移 \(f_x = \max(f_{ch_{x,0}},f_{ch_{x,1}}) + 1\)。

D. Frequency Problem \(\color{red}{\times}\)

发现不了性质。

结论：答案区间的众数一定包含全局众数。

考虑对于当前区间 \([l,r]\) 的众数是 \(p,q\)，全局众数是 \(x\)。我们考虑让这个区间包含 \(ct_p\) 个 \(x\)，如果现在众数出现次数变多了，那就增加 \(x\) 的出现次数。容易发现，这个过程中答案变得不劣。

对于 D1，直接枚举另一个众数 \(y\) 的值，找出最长的 \(x,y\) 出现次数相同的区间。这里我们不需要判断 \(x,y\) 是否是众数，因为真实答案不劣。复杂度 \(\mathcal O(na_i)\)。

对于 D2，考虑根号分治。出现次数大于 \(\sqrt n\) 的只有 \(\mathcal O(\sqrt n)\) 个，可以直接用 D1 的做法；对于出现次数小于 \(\sqrt n\) 的数，我们枚举出现次数，并控制 \(x\) 的出现次数即可。

CF1558

A. Charmed by the Game \(\color{green}{\checkmark}\)

分第一局为 Alice 和第一局为 Bob 讨论，然后枚举 Alice,Bob 在先手赢了几局即可。

B. Up the Strip \(\color{green}{\checkmark}\)

容易写出 DP 方程：\(f_i = \sum \limits_{j=2}^i f_{\lfloor\frac{i}{j}\rfloor} + \sum \limits_{j=1}^{i-1}f_j\)，直接整除分块的复杂度是根号，过不了。

考虑 \(f_j\) 对后面 \(f_i\) 的贡献，枚举 \(\lfloor \dfrac{i}{j}\rfloor = k\)，容易发现满足条件的 \(i\) 是一段区间，差分即可。复杂度调和级数。

C. Bottom-Tier Reversals \(\color{green}{\checkmark}\)

比较简单的构造题。

首先观察到位置的奇偶性不变，所以如果 \(p_i,i\) 的奇偶性不同直接无解。注意到翻转 \([1,p]\) 不会改变 \([p+1,n]\)，考虑增量构造，将 \(n,n-1,\ldots,2\) 依次放到位置上。

枚举 \(x = n,n-2,\ldots,3\)，一次性将 \(x,x-1\) 填入。最开始形如 \([\ldots,x,\ldots,x-1,y,\ldots,x+1,x+2,\ldots,n-1,n]\)。先将 \(x\) 翻转到 \(x-1\) 前面，然后翻转 \(y\)，序列形如 \([y,x-1,x,\ldots,]\)，然后翻转 \(x\)，再翻转到目标位置即可。需要用 \(5\) 次操作填入两个位置，满足限制。

D. Top-Notch Insertions \(\color{red}(\checkmark)\)

不困难的题，看完题说「要是 vp 的时候开了这题就过了」，但是实际上自己写和调了 3h，码力不足。

考虑插入排序后形成的最终不降数组，则每一个 \(i\) 和 \(i+1\) 之间的关系可能是严格小于或小于等于。考虑怎么计数，这是一个经典问题，设有 \(c\) 个小于等于号，我们将小于等于号后面的数字加 \(1\)，现在值域变成了 \(n+c\)，要求有多少严格递增序列长度为 \(n\)，值域为 \(n+c\)，插板容易求出答案。

问题在于怎么求出来 \(c\) 的值。很明显可以顺序插入 \(1\ldots n\)，插入数字后如果它不再末尾，将它设置成 \(<\) 且前面的设置为 \(\le\)。

但是我们复杂度不能乘 \(n\)，只可以与 \(m\) 有关，这是比较烦人的。考虑平衡树维护，插入一个 \((x,p)\) 时相当于 \(x\) 的最终下标是 \(p\)，同时给后面的所有下标 \(+1\)。然后查看平衡树里的前驱是否真的是前驱，如果是，把 \(\le\) 改成 \(<\)。这样的复杂度是 \(\mathcal O(m \log n)\)。

F. Strange Sort \(\color{red}{\times}\)

精妙的转化。

考虑对排列排序比较麻烦，不妨对 \(k = 1,2,\ldots,n\) 都执行：

• \(b_i = [a_i \ge k]\)，然后对序列 \(b\) 执行上述排序，得到答案 \(res_k\)。

最终的答案即为 \(\max \limits_{k=1}^n res_k\)。

考虑怎么求单个 \(res_k\)，设计 DP。我们需要让每一个 \(0\) 都到所有 \(1\) 左边。设第 \(i\) 个 \(0\) 归位的最小次数是 \(f_i\)，其左边有 \(c_i\) 个 \(1\)，则 \(f_i = \max(f_{i-1}+1,c_i + (pos_i \bmod 2))\)，含义是如果中途撞到 \(0\) 则答案就是上一个 \(0\) 的代价 \(+1\)，否则就是 \(1\) 的数量加上第一次不能操作的开销。

这里注意到我们只关心 \(f_m\)，因此将上式递归带入后得到 \(res_k = \max(c_i + (pos_i \bmod 2) + (m - i))\)。

因此按 \(k = 1,2,\ldots,n\) 顺序遍历后线段树维护 \(res\) 即可。

CF1528

第一次在 div1 切掉 4 题，纪念一下，虽然是 vp。

A. Parsa's Humongous Tree \(\color{green}{\checkmark}\)

感受那股劲，每个点取端点一定不劣，然后树 DP。

B. Kavi on Pairing Duty \(\color{green}{\checkmark}\)

感觉这是个困难题啊，被卡了 30+ mins。

考虑 DP，设 \(f_i\) 表示 \(i\) 个点的线段的方案数，答案是 \(f_{2n}\)。显然 \(\forall i \bmod 2 = 1,f_i = 0\)。

对于 \(i \bmod 2 = 0\)，分讨：

• 其内部的线段没有再嵌套，此时每条线段长度相等。手画一下发现长度 \(j\) 合法的条件是 \(i \bmod (2j) = 0\)。
• 其内部还有线段。此时 \(f_i \gets f_i + \sum \limits_{j=1}^{i-1}f_j\)。

注意到第一个即为偶约数个数，预处理即可。

C. Trees of Tranquillity \(\color{green}{\checkmark}\)

考虑两个条件的限制：

• \(S\) 中的点必须在第一棵树上一条到根链上。
• \(S\) 中任意两点 \(u,v\) 不能在第二棵树上一条到根链上。

贪心的，如果第二棵树上一条到根链出现多个点，保留最下面的。

因此 dfs 遍历第一棵树，在第二棵树上做链推平，求和，撤销，线段树即可。撤销的话只需要在每次修改时都记录下来，然后退栈。注意空间。

D. It's a bird! No, it's a plane! No, it's AaParsa! \(\color{green}{\checkmark}\)

最后 30min 秒掉了，感觉真的比 B 还简单。

对每个节点跑 \(\mathcal O(n^2)\) 的 dj。

因为可以停留，我们希望到每个点越早越好。到 \(u\) 后，根据 \(dis_u\) 判断每条边现在指的点 \(v\)，把它挂到 \(v\) 处，把取模的权值拆开后边权应为 \(w-v\)。顺序遍历 \(v = 1,2,\ldots,2n\)，每次加入挂在这个点的边权，得到集合最小值，然后用 \(mn+dis_u+v\) 更新 \(dis_v\) 即可。

E. Mashtali and Hagh Trees \(\color{red}{\times}\)

观察性质，满足第三条限制的树只有以下三种：叶向树、根向树、同根的叶向树和根向树拼起来的结果。

前两部分除去根的方向没有区别，计算出一个即可。

设 \(f_i\) 表示最长链长度为 \(i\) 的外向树且合法方案数，我们转移时考虑建一个新点然后往上面拼子树。由于会多出一条根连向儿子的边，因此我们钦定根的度数不超过 \(\textbf 2\)。

考虑转移，枚举根的度数。

• 度数为 \(1\)，此时直接就是 \(f_{i-1}\)。
• 度数为 \(2\)。此时我们要求两个子树至少有一个链长是 \(i-1\)，因此设 \(s_i = \sum \limits_{j = 1}^i f_j\)，我们先算出子树长度任意的方案树，然后减去链长都小于 \(i-1\) 的方案数，即 \(\dbinom{s_{i-1}+1}{2}-\dbinom{s_{i-2}+1}{2}\)。

求出 \(f_n\) 后，给答案加上 \(\dbinom{s_{n-1}+2}{3} - \dbinom{s_{n-2}+2}{3}\)，即根的度数为 \(3\) 的方案数，记这个值为 \(ans\)，贡献为 \(2ans \color{red}-1\)，这是因为内向链和外向链同构。

考虑第三种情况：（图来自题解区）

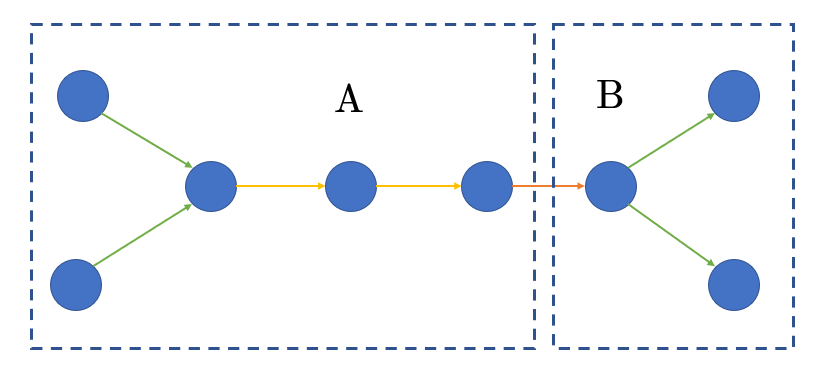
强制 B 部分的根度数为 \(\textbf{2}\)，记根为 \(2\) 的外向树数量为 \(g_i\)。枚举 A 部分的链长为 \(i\)，则贡献 \(g_{n-i-1}(f_i\color{red}-1\color{black})\)，原因是如果左侧是一条链整棵树会变成外向树。

因此给刚才的 \(2ans-1\) 再加上 \(\sum\limits_{i} g_{n-i-1}(f_i-1)\) 即可，时间复杂度线性。

CF1798 (Div.2)

笑点解析：div2 过了 3 个题，rank 3000+ 。

A. Showstopper \(\color{green}{\checkmark}\)

B. Three Sevens \(\color{green}{\checkmark}\)

直接模拟即可。

C. Candy Store \(\color{green}{\checkmark}\)

贪心的让 \(c_i\) 和 \(c_{i-1}\) 相同，如果不能相同就再开一段。

首先求 \(l = \operatorname{lcm}(c_{i-1},b_i)\)，则需要给这一段的每一个数字都乘 \(\dfrac{l}{c_{i-1}}\)，这个只需要维护 \(\gcd(\dfrac{a_i}{c_i})\)，然后再判以下 \(\dfrac{l}{b_i}\) 是否是 \(a_i\) 的因数即可，将其加入 \(\gcd\)。

D. Shocking Arrangement \(\color{red}{\times}\)

考虑转化条件，问题等价于前缀和的极差小于原序列的极差。

直接随便加，对 \(a\) 排序后，如果加最大的前缀和小于 \(\max\) 就加，否则加最小的。容易证明其合法。

E. Multitest Generator \(\color{red}(\checkmark)\)

简单的观察性质题，可惜 vp 时时间不够了。

• 观察 \(1\)：答案永远 \(\le 2\)。
  • 我们可以 \(a_1 \gets 1,a_2 \gets n - 2\)。

那我们分讨答案。

• 若答案为 \(0\)，则要求 \(a_2,\ldots,a_n\) 恰好可以划分成 \(a_1\) 个 test。
• 若答案为 \(1\)，则至少满足以下其一：
  • \(a_2,\ldots,a_n\) 可以划分为若干个合法 test，此时只需要修改 \(a_1\)。
  • \(a_2,\ldots,a_n\) 可以在 \(1\) 次修改后变成 \(a_1\) 个 test。
• 否则答案为 \(2\)。

容易想到设 \(f_i\) 表示以 \(i\) 结尾的后缀可以划分的 test 个数，如果不合法 \(f_i = -\inf\)。但是我们发现只用 \(f\) 无法处理情况 \(2.2\)。这里我们需要一个观察：

• 观察 \(2\)：对于情况 \(2.2\)，我们只关心可以达到的最大 test 数量。
  • 可以通过合并 test 将 test 数量调整至符合要求。

那么设 \(g_i\) 表示可以修改 \(1\) 个的最大划分 test 数量，有 \(g_i = \max(\max\limits_{j>i}\{f_j\}+1,g_{i+a_i+1}+1)\)。维护 \(f_i\) 的后缀 \(\max\) 即可做到线性。

F. Gifts from Grandfather Ahmed \(\color{red}{\times}\)

结论题。

定理：从 \(2n-1\) 个数字中一定可以选出 \(n\) 个和为 \(n\) 的倍数的数。

然后将 \(s_i\) 最大的使用额外的盒子，剩余的跑背包，时间复杂度 \(\mathcal O(n^3)\)。

CF1975（Div.1+2）

A. Bazoka and Mocha's Array \(\color{green}{\checkmark}\)

B. 378QAQ and Mocha's Array \(\color{green}{\checkmark}\)

最小值一定要包含。

把不是最小值倍数的取 \(\gcd\) 看一下是否在数组里即可。

C. Chamo and Mocha's Array \(\color{green}{\checkmark}\)

容易发现如果存在区间 \([l,r]\) 使得 \(x\) 是中位数，那么最后答案就可以是 \(x\)。

二分答案判定即可。

D. Paint the Tree \(\color{green}{\checkmark}\)

贪心的，让红点和蓝点直线相遇，然后跟着红点遍历整棵树。

E. Chain Queries \(\color{green}{\checkmark}\)

条件等价于存在一条路径覆盖所有黑点且路径长度恰为黑点数量。

线段树维护第一个条件是经典套路了，第二个条件最后算一下距离就行。

F. Set \(\color{red}{\times}\)

唐氏搜索题，但是我咋比这个题还唐啊？？？

考虑在 \(0 \sim 2^n - 1\) 的 trie 树上深搜 \(s\) 的值，设当前还剩 \(i\) 位未确定。记 \(m = 2^i\)，我们要维护数组 \(v_0,v_1,\ldots,v_{m-1}\)，\(v_x\) 表示剩余部分填 \(x\) 后 \(|s \cap t|\) 的合法值。

考察 \(s\) 的第 \(i\) 位填写什么值：

• 如果填 \(0\)，则需要把 \(v_j\) 和 \(v_{j+m}\) 的限制合并，原因是 \(i-1\) 及以下的位怎么填 \(|s \cap t|\) 和 \(|s \cap (t+m)|\) 的值都相同，因此需要合并限制。
• 如果填 \(1\)，则需要把 \(v_j\) 和 \(v_{j+m} >> 1\) 的限制合并，原因是 \(i-1\) 及以下的位怎么填 \(|s \cap t|\) 都比 \(|s \cap (t+m)|\) 的值少 \(1\)，因此右移掉末尾一位。

最终搜索到叶子时，判断一下 \(0\) 位是否合法即可。复杂度 \(\mathcal O(n2^n)\)。

CF1977 （Div.2）

A. Little Nikita \(\color{green}{\checkmark}\)

B. Binary Colouring \(\color{green}{\checkmark}\)

先将 \(x\) 转二进制，考察从低到高遍历，对于一段连续的 \(1\) 形如 \(0111110\)，把它变成 \(0,-1,0,0,0,0,1\)。如果出现 \(1,-1\)，就变成 \(-1,0\) 即可。

C. Nikita and LCM \(\color{red}{\times}\)

考虑一个简单情况：如果序列的 \(\operatorname{lcm}\) 大于最大值，那么答案是 \(n\)。否则，\(\operatorname{lcm}\) 只能是最大值的因数，直接 DP 即可。

D. XORificator \(\color{red}{\times}\)

唐氏题，但是我咋比这题还唐啊？？？

一个比较重要的观察是，使得一列变得合法的操作只有 \(\mathcal O(n)\) 种。

然后做完了。

注意 \(10^9\) 级别模数的单哈希会被卡。

E. Tensor \(\color{green}{\checkmark}\)

https://www.luogu.com.cn/article/huleeulw

CF1919 （Div.1 + 2）

A. Wallet Exchange \(\color{green}{\checkmark}\)

B. Plus-Minus Split \(\color{green}{\checkmark}\)

观察样例并合理猜测，最优解形如每个符号划一段，输出数量的差的绝对值即可。

C. Grouping Increases \(\color{green}{\checkmark}\)

直接嗯贪，维护两个结尾，如果只有一个序列填了答案不增加就填上，否则填在小的那个后面。

D. 01 Tree \(\color{red}{\times}\)

观察，再观察。

考虑对于两个父亲相同的叶子，其权值一定是 \(w,w+1\)，且 \(w\) 是其父亲的权值。我们删去这两个叶子并加入 \(w\) 表示其父亲成为新的叶子。

我们需要知道哪两个叶子相邻，这里需要另一个观察：选择最大的。容易发现如果合法，最大值的旁边一定还有叶子。

注意到最大值不一定唯一，找到一个最大值连续段，其前驱后继至少有一个 \(mx - 1\)，链表维护顺序即可。

注意 \(0\) 需要恰好有一个，需要特判。

E. Counting Prefixes \(\color{red}{\times}\)

神秘的思路，想不到一点。

考虑枚举序列的和 \(s\)，先构造序列 \([1,1,1,\ldots,1,-1,\ldots,-1]\)，其中 \(1\) 有 \(p_n\) 个，\(-1\) 有 \(p_n - s\) 个。

一个神秘的思路是，从大到小使得前缀和 \(x\) 合法，在前缀和 \(x\) 处不断插入 \(-1,1\)，使得 \(x\) 数量增加 \(1\)，\(x-1\) 的数量也增加 \(1\)。因此，若 \(x\) 出现了 \(y\) 次，则插板容易得到方案数量。

我们可以 \(\mathcal O(n)\) 计算一个 \(s\)，枚举 \(\mathcal O(n)\) 个 \(s\) 即可。

F1. Wine Factory (Easy Version) \(\color{green}{\checkmark}\)

容易发现酒量就是 \(\sum a_i\) 减去最后的水量，设水量 \(x\)，则过一个 \((a_i,b_i)\) 相当于 \(x \gets \max(x+a_i-b_i,0)\)，维护矩阵 \(\begin{bmatrix}x & 0 \end{bmatrix}\)，每次相当于做 \((\max,+)\) 的矩阵乘法，给每个位置赋矩阵 \(\begin{bmatrix}a_i-b_i & -\infty\\0 & 0 \end{bmatrix}\) 即可，线段树维护矩阵乘积。

CF1794 （Div.2）

A. Prefix and Suffix Array \(\color{green}{\checkmark}\)

容易发现只需要寻找长度为 \(n-1\) 的串。

B. Not Dividing \(\color{green}{\checkmark}\)

如果 \(a_{i-1} \ne 1\)，最多让 \(a_i\) 自增一次就能合法。

C. Scoring Subsequences \(\color{green}{\checkmark}\)

唐氏贪心题。容易发现答案是一段后缀，二分一下即可。

D. Counting Factorizations \(\color{green}{\checkmark}\)

考虑设 \(a_i\) 为第 \(i\) 个质因子，\(b_i\) 为第 \(i\) 个质因子的出现次数。对于非质数，其只能出现在次数上。对于一组选择，设次数的出现次数为 \(c_1,\ldots,c_k\)，次数的排列方案为 \(\dfrac{n!}{c_1!c_2!\ldots c_k!}\)

设 \(f_{i,j}\) 表示考虑了前 \(i\) 个质因子，已经选择了 \(j\) 个，转移是 \(f_{i,j} = (b_i - 1)!^{-1}f_{i-1,j-1} + (b_i)^{-1}f_{i-1,j}\)，最后输出 \(f_{ct,n}\) 即可。

E. Labeling the Tree with Distances \(\color{red}{\times}\)

树哈希，设计哈希函数 \(f(T) = \sum ct_i \times base^i\)，其中 \(ct_i\) 是深度为 \(i\) 的点的数量。

这样设计函数的用意有两个，一是方便换根求出所有哈希值，二是可以直接与给出的深度数组对比。

由于只给出了 \(n-1\) 个点，我们判断时与预定的哈希值做差，判断剩余的是否是 \(base\) 的次幂即可。

CF1743 （Edu Div.2）

A. Password \(\color{green}{\checkmark}\)

B. Permutation Value \(\color{green}{\checkmark}\)

答案的下界显然是 \(2\)。

排列 \(1,n,\ldots,2,3,\ldots,n-1\) 即可达到这一下界。

C. Save the Magazines \(\color{green}{\checkmark}\)

对于一段连续的 \(1\)，其可以选择放弃覆盖中间的某一个并覆盖前面那个 \(0\)。因此把 \(0\) 的权值和区间 \(\min\) 比较一下即可。

D. Problem with Random Tests \(\color{green}{\checkmark}\)

做麻烦了，哈哈。

首先有个显然的贪心：一个串必定是原串，否则最高位不优。

然后发现另一个串必定是一个前缀。

赛时的做法是，枚举最多有几个 \(0\) 能变成 \(1\)，这会要求存在一个子串满足对应位置全 \(1\)。由于数据随机的性质，这样暴力的复杂度正确。

当然一个更明智的做法是，直接暴力把 \(n\) 个前缀都尝试一次，暴力比较字典序。由于数据随机，复杂度正确。

E. FTL \(\color{red}{\times}\)

看了题解第一句话就会了，哎。

一个重要的观察是：执行完两个武器一起攻击后，问题变成了一个规模更小的子问题。

因此就可以设计 DP 了，即 \(f_i\) 表示怪物剩余 \(x\) 滴血，且两个武器都刚刚进入冷却期的最小代价。

考虑转移，枚举连续使用第 \(k\) 个武器 \(j\) 次，需要的时间是 \(jt_k\)，而这个时间可以进行 \(l = \dfrac{jt_k}{t_{1-k}}\) 次 \(1-k\) 武器攻击，其中最后一次攻击可以两个一起，因此伤害要减去 \((l + j - 1)s\)。

时间复杂度即为 \(\mathcal O(n^2)\)。

F. Intersection and Union \(\color{green}{\checkmark}\)

好像也做麻烦了？

关于连续做多次位运算，一个常见的套路是考虑最后一次推平操作。比如，\(\operatorname{or} 1,\operatorname{and} 0\) 都是推平操作，而 \(\operatorname{or} 0,\operatorname{and} 1\) 则是无效操作。异或我们暂时不管。

我们拆位考虑每一位的贡献，考虑每一位有多少种情况可以在最后的集合中为 \(1\)，把所有位的方案数加起来即为答案。

倒序考虑每一条线段 \([l_i,r_i]\)，钦定它有效，则首先有了 \(3^{i-2}\) 种确定前面符号的方案。考虑后面的所有 \(0\)，他们可以自由选择 \(\operatorname{or}\) 或 \(\operatorname{xor}\)，而对于 \(1\)，我们需要选择特定奇偶个做 \(\operatorname{xor}\) 以保证最终结果是 \(1\)。由于 \(\dbinom{n}{0} + \dbinom{n}{2} + \ldots + \dbinom{n}{n - n \bmod 2} = 2^{n-1}\)，故方案数量为 \(2^{n-i-1}\)。注意特判后面没有 \(1\) 的情况，此时次幂不 \(-1\)。这样的时间复杂度是 \(\mathcal O(n^2)\)。

考虑优化：我们只需要把所有位一起考虑，用线段树维护每个位的系数再求和即可。时间复杂度 \(\mathcal O(n \log n)\)。

G. Antifibonacci Cut \(\color{red}{\times}\)

首先有显然的 \(\mathcal O(m)\) 空间的 DP 做法。

注意到 \(\forall i > 1,f_i\) 是 \(f_{i+1}\) 的前缀，因此我们把所有 \(f_i \; (i > 1)\) 拼起来称作串 \(t\)。

核心结论：对于固定的右端点 \(r\)，只有 \(\mathcal O(\log m)\) 个左端点 \(l\) 满足 \(s[l,r]\) 是 \(t\) 的前缀。

官方题解也没有给出正式证明，只是打表验证。

考虑用 bitset 存下 \(s,t\)，直接维护这 \(\mathcal O(\log m)\) 个左端点和其对应的 DP 值，每加入一个新的字符，将其丢进左端点集合，并判断给每个左端点拼上这个字符后是否仍是 \(t\) 的前缀。时间复杂度 \(\mathcal O(m \log m)\)，空间复杂度 \(\mathcal O(\dfrac{m}{w})\)。

CF1778 （Div.2）

集爆搜、大型推柿子、板子、巨多细节题于一场，非常好的组题！

不补这场 D。

A. Flip Flop Sum \(\color{green}{\checkmark}\)

B. The Forbidden Permutation \(\color{green}{\checkmark}\)

容易有贪心：只考虑打破 \(a_i,a_{i+1}\) 的限制即可。计算每一对 \(a_i,a_{i+1}\) 的限制只需要简单分讨。

C. Flexible String \(\color{green}{\checkmark}\)

喜欢出爆搜？

E. The Tree Has Fallen! \(\color{green}{\checkmark}\)

喜欢出板子？

通常换根子树的处理策略都是把新的子树对应到原来的子树上，新子树有 \(3\) 种情况：全局、原子树和全局除掉原节点某个儿子的子树，这些都可以拆到 dfn 区间上。

然后直接变成 CF1100F 了，线性基解决。

F. Maximizing Root \(\color{red}{(\checkmark)}\)

【】DP 题。码题十分钟，调题一小时。

考虑最终的 \(\gcd\) 一定是 \(a_1\) 的因数，因此我们设 \(f_{i,j}\) 表示 \(i\) 的子树内 \(\gcd\) 是 \(j\) 的倍数的最小代价，注意只有 \(\mathcal O(d)\) 个有效状态。

进入 \(u\) 时，我们首先将 \(a_u\) 的因数 dp 值赋 \(0\)。考虑一个一个子树合并，即 \(\operatorname{chmin}(f_{u,\gcd(i,j)},f_{u,i} + f_{v,j})\)。这时我们得到了不在 \(u\) 做乘法的答案，只需要考虑乘法的贡献即可（注意 \(u = 1\) 时不能做这个转移）。

复杂度即为 \(\mathcal O(nd^2)\)，注意求 \(\gcd\) 的次数非常多而值域很小，故需要先 \(\mathcal O(V^2 \log V)\) 预处理后 \(\mathcal O(1)\) 查询。

CF1696（Div.1+2）

不做这场 C。

A. NIT orz! \(\color{green}{\checkmark}\)

B. NIT Destroys the Universe \(\color{green}{\checkmark}\)

注意到可以通过 \([1,n]\) 消灭所有 \(0\) 或者全都变成 \(0\)，故答案不超过 \(2\)。简单分讨即可。

D. Permutation Graph \(\color{green}{\checkmark}\)

考虑一个贪心：每次走合法的最远的。它看起来很对，实际上也很对。

接下来问题是对于 \(i\) 怎么找这个最远的，不妨找到第一个小于它的位置 \(r\)。我们不断跳第一个大于当前值的位置，直到这个位置大于 \(r\)，小于同理。复杂度均摊线性。

E. Placing Jinas \(\color{green}{\checkmark}\)

容易发现 \((i,j)\) 需要操作的次数是 \(\dbinom{i + j}{i}\)，上指标求和即可。

F. Tree Recovery \(\color{red}{\times}\)

考虑如果我们已经知道一条边 \((u,v)\)，则可以根据 \(v\) 的所有和 \(u\) 距离相同的点，确定 \(v\) 的所有出边。

那么直接枚举一条边 \((1,i)\) 并 check，时间复杂度 \(\mathcal O(n^4)\) 可以通过。

CF1984（Div.1+2）

A. Strange Splitting \(\color{green}{\checkmark}\)

B. Large Addition \(\color{green}{\checkmark}\)

降智了，卡了好久。

注意到一个数字合法的充要条件是，\(s_0 = 1,s_{n} \ne 9\) 且中间没有 \(0\)。

C. Magnitude \(\color{green}{\checkmark}\)

降智了，又卡了好久。

注意到我们只关心 \(c\) 的最值，因此设计 DP：\(f_i,g_i\) 分别表示到 \(i\) 且能到达的最大最小值，\(gf_i,gg_i\) 表示对应的方案数。\(f,g\) 的转移是简单的，\(gg\) 的转移只需要考虑是否使用 \(\operatorname{abs}\) 的答案是否相同，\(gf\) 的转移考虑选 \(f,g\) 哪个更大，如果一样注意如果 \(f,g\) 相同不要算重。

D. "a" String Problem \(\color{green}{\checkmark}\)

考虑找到第一个 \(s_{p} \ne \texttt a\) 的位置 \(p\)，则 \(t\) 形如 \(\texttt{aa}\ldots\texttt{a}+s_{p\ldots q}\)。直接枚举 \(q\)，考虑这个 \(q\) 对应的 \(t\) 前面能拼接几个 \(\texttt{a}\)。

考虑如何求这个值。对于一个非 \(\texttt{a}\) 值，其必须完全匹配 \(s_{p\ldots q}\)，可以用 Z 函数快速判断。如果这个值是 \(\texttt{a}\) 则直接跳过。最大拼接 \(\texttt a\) 的数量就是两两匹配之间 \(\texttt a\) 的最小值。

由调和级数容易分析复杂度是 \(\mathcal O(n \log n)\)。

E. Shuffle \(\color{red}{\times}\)

需要惊人的注意力。

结论：答案是去掉每个叶子后的最大独立集的最大值 \(+1\)。

• 必要性：对于非根节点，在原树上有边相连的两点 \((u,v)\) 不可能同时是叶子。
  • 假设 \(u\) 比 \(v\) 先选出来做根，此时 \(u\) 一定不是叶子。
• 充分性：手玩一下吧，我也不知道怎么严谨的证明。

考虑怎么求出来这个，看看做题笔记 III 的 \(\color{blue}(163)\) 吧。

F. Reconstruction \(\color{red}{\times}\)

看了一个 Hint 就会了，怎么回事呢。

Hint：考虑相邻元素的限制。

设 \(sum\) 表示整个序列的和。

• \(\texttt{PP}\)：\(|a_i - a_{i-1}| \le m\)。
• \(\texttt{SS}\)：\(|a_i - a_{i-1}| \le m\)。
• \(\texttt{PS}\)：\(a_i + a_{i-1} = sum\)。
• \(\texttt{SP}\)：\(|a_i - (sum - a_{i-1})| \le 2m\)，也即 \(|a_i + a_{i+1} - sum| \le 2m\)。

考虑枚举第一个 \(\texttt{PS}\) 的位置以确定 \(sum\)，然后根据上述四个条件做 DP 即可。

每次 DP 的复杂度线性，总复杂度 \(\mathcal O(n^2)\)。

G. Magic Trick II \(\color{red}{\times}\)

• 重要观察：答案至少是 \(n - 3\)。
• 直接通过构造证明。

\(k = n,n-1\) 的情况是简单的。

考虑 \(n\) 是奇数的情况，此时我们有答案至少是 \(n - 2\)。

考虑把数组看作一个环，一次操作看作对这个环的修改，同时维护终止位置 \(ed\)。

考察我们实质上操作能干什么：

• 将 \(ed\) 移动两位。例如 \([1,2,3,4,5|] \to [4,5,1,2,3]([1,2,3|4,5])\)。
• 将 \(ed\) 两侧的元素交换，同时移动一位。例如 \([1,2,3,4,5|] \to [1,5,2,3,4]([5,2,3,4|1])\)。

那么由于 \(n\) 是奇数，我们可以通过操作 \(1\) 将 \(ed\) 移动到任意位置，并用操作 \(2\) 移动元素。那么从 \(n\) 到 \(1\) 依次归位即可。

\(n\) 是偶数时一个 naive 的思路是取 \(k = n - 3\)，将 \(n\) 归位后变成奇数的情况。

但是有一些情况我们可以用 \(k = n - 2\) 解决，这种情况是逆序对有偶数个。

我们考虑当 \(ed\) 和 \(pos_i\) 奇偶性不同的处理方法，以数组 \([1,2,3,\color{red}{4,5,6}\color{black}]\) 举例，我们当前要把某个数字放到位置 \(3\)。

• 如果在位置 \(3\)，那么直接不用管。
• 如果在位置 \(2\)，我们先将其调到 \(1,2\) 之间并交换，转化为位置 \(1\) 的 case。
• 如果在位置 \(1\)，将 \(ed\) 放置在 \(2,3\) 中间交换改变奇偶性即可。

然后就做完了，细节特别多，唉。

CF1523（Div.1+2）

A. Game of Life \(\color{green}{\checkmark}\)

注意到有用的操作是 \(\mathcal O(n)\) 级别的，直接模拟即可。

B. Lord of the Values \(\color{green}{\checkmark}\)

先解决 \(n = 2\)：\((a_1,a_2) \to (a_1 + a_2,-a_1) \to (a_2,-a_1) \to (a_2-a_1,-a_2) \to (-a_1,-a_2)\)。

然后由于 \(n\) 是偶数，两两之间做即可。

C. Compression and Expansion \(\color{green}{\checkmark}\)

直接贪心的留下更多的 \(\texttt{.}\) 不劣。

D. Love-Hate \(\color{green}{\checkmark}\)

看到保留至少一半想到随机化：随机选取一个 \(i \in [1,n]\)，其有 \(\dfrac{1}{2}\) 的概率包含在答案里。

考虑只保留第 \(i\) 个人有的 \(p\) 位，剩余的问题是每个人给自己子集 \(+1\)，合法的是值 \(\ge \dfrac{n}{2}\) 的，直接高维前缀和即可。

E. Crypto Lights \(\color{red}{\times}\)

精彩的转化。

考虑写出期望的表达式：\(E = \sum\limits_{i=1}^n i \cdot p_i\)，对 \(p_i\) 求后缀和记为 \(s\)，则式子转化为 \(E = \sum s_i\)。

考虑 \(s_i\) 的实际含义：在 \(i\) 之后出现不合法的所有概率之和，等价于到达 \(i - 1\) 时刻仍然合法。也就是 \(s_i\) 是在 \(1,2,\ldots,n\) 中选择 \(i-1\) 个数且相邻数字差大于 \(k\) 的方案数。

这个东西相当于插长度为 \(k\) 的板，类似插板法求答案。

G. Try Booking \(\color{red}{\times}\)

• 观察：对于一个 \(x\)，只会选择 \(\dfrac{n}{x}\) 个区间，所有 \(x\) 选择的区间数量和是 \(\mathcal O(n \log n)\) 的。

对于一个固定的 \(x\)，其被选择区间隔开形成的空闲区间也是 \(\mathcal O(\dfrac{n}{x})\) 个。

设计 \(sol(l,r)\) 表示当前 \([l,r]\) 区间空闲，只需要找到 \(l \le x,y \le r\) 的事件 \((x,y)\) 的最小 id，然后递归 \(sol(l,x-1),sol(y+1,r)\)，树套树即可。

扫描线实现加点，复杂度 \(\mathcal O(n \log^3 n)\)。

CF1503（Div.1）

草你吗啊，破防了，，，

A. Balance the Bits \(\color{red}{\times}\)

什么人类智慧题，，

首先有解的充要条件显然：有偶数个 \(1\) 且 \(s_1 = s_n = 1\)。

然后对于 \(1\)，前一半填左括号，后一半填右括号。

对于 \(0\)，左右括号交替填。

结束。

B. 3-Coloring \(\color{green}{\checkmark}\)

考虑染色法，给 \((i,j)\) 染色 \((i+j) \bmod 2+1\)。这样的问题是交互库可以一直不让我们染某种颜色，此时一定是一种颜色已经填满，那么填颜色 \(3\) 即可。

C. Travelling Salesman Problem \(\color{red}{\times}\)

注意到 \(\sum c_i\) 是必须要付出的，我们希望让额外代价尽可能小。

你可能会有若干符合直觉的想法：直接降序排，只需要最后一次付额外代价；直接升序排，等等。但是这些都不对。

给 \(c_i\) 找一个实际含义：从 \(i\) 出发可以不付代价到达 \(a_j \in [0,a_i + c_i]\) 之间的 \(j\)。

考虑按 \(a\) 升序排序后从 \(1\) 出发，维护 \(a_i + c_i\) 的 \(\max\)。顺序遍历 \(1 \sim n\)，如果发现 \(a_i\) 大于前面所有 \(a_j + c_j\) 则必须付出代价。只走这些必须付出代价的，然后免费走到 \(n\) 后再免费返回即可。

时间复杂度除排序外线性。

D. Flip the Cards \(\color{red}{\times}\)

寻找有解条件，容易发现一个显然的必要条件：不存在 \(i\) 满足 \(a_i,b_i \le n\)。存在这种情况会导致还需要 \(n - 1\) 个小于等于 \(n\) 的数字，但是由于存在 \(a_i,b_i\) 导致最多有 \(n - 2\) 个。

那么现在所有 \((a_i,b_i)\) 都满足 \(\min(a_i,b_i) \le n,\max(a_i,b_i) > n\)，考虑设 \(f_i\) 表示 \(i\) 对应的数字。寻找合法的充要条件：

• 充要条件：\(\{f_i\}\) 可以划分为两个下降子序列。
• 充分性：注意到 \(f_i > n\)，可以将第二个下降序列以 \((f_i,i)\) 的形式拼在第一个后面。
• 必要性：额。

当然我们还要最优化，考察一些特殊的决策点：满足 \(\min\limits_{i=1}^{j-1} f_j > \max \limits_{i=j+1}^n f_j\) 的点 \(j\)，以这些位置将序列划分为若干段，则段之间可以自由拼接，段中的划分方式唯一。因此每段最优化后加起来即可。

CF1978（Div.2）

第一场 AK 的 Div.2，纪念一下。

A. Alice and Books \(\color{green}{\checkmark}\)

B. New Bakery \(\color{green}{\checkmark}\)

答案随 \(k\) 是二次函数，直接三分求 \(\max\) 即可。

C. Manhattan Permutations \(\color{green}{\checkmark}\)

\(k\) 是奇数显然无解。

和出题人对脑电波，一种合法构造是如果交换 \(i,p\) 不会使得答案大于 \(k\) 就交换，初始时 \(p = n\)，每完成一次交换 \(p \gets p - 1\)。

D. Elections \(\color{green}{\checkmark}\)

考虑对于 \(i\)，如果它不能赢，那么需要清除掉前面所有元素使得中立的人投给他。

如果这还不够，就把后面的 \(\max\) 投给他，结束。

E. Computing Machine \(\color{green}{\checkmark}\)

注意到我们一定是贪心的先把 \(b\) 尽可能的填 \(1\)，再把 \(a\) 尽可能的填 \(1\)。然后注意到 \([l,r]\) 的答案和 \([1,n]\) 的答案只差在位置 \(l,l+1,r-1,r\)，这些位置暴力计算后，剩余位置前缀和即可。

F. Large Graph \(\color{green}{\checkmark}\)

注意到表格形如：

1234
4123
3412
2341

由于 \(k \ge 2\)，因此如果 \(a_i \ge 2\) 则一条对角线总在一个连通块中，因此我们实际上得到了一个由 \(2n-1\) 条对角线组成的新数组，这个问题转化到了数列上。我们只需要枚举质因子 \(w\)，对其倍数合并即可。每个元素只会被枚举 \(\mathcal O(\log n)\) 次，因此复杂度 \(\mathcal O(n \log^2 n)\)。

CF1637（Div.1+2）

A. Sorting Parts \(\color{green}{\checkmark}\)

B. MEX and Array \(\color{green}{\checkmark}\)

对每个子区间嗯 DP 即可。复杂度 \(\mathcal O(n^4)\)。

C. Andrew and Stones \(\color{green}{\checkmark}\)

差点没做出来这题 /hsh

考虑大部分情况，只要存在一个非 \(1\) 元素就可以用它周转存在解。

此时每个奇数元素需要传递一个 \(1\)，答案是 \(\sum \lceil \dfrac{a_i}{2} \rceil\)。

无解情况只有全 \(1\) 和 \(n = 3\) 且中间的是奇数。

D. Yet Another Minimization Problem \(\color{green}{\checkmark}\)

平方拆开，代价是 \(\sum (n-2)(a_i^2 + b_i^2) + (\sum a_i)^2 + (\sum b_i) ^ 2\)。直接设 \(dp_{i,j}\) 表示 \(\sum a = i,\sum b = j\) 是否可以达到，bitset 优化之，复杂度 \(\mathcal O(\dfrac{n^5}{w})\)。

E. Best Pair \(\color{green}{\checkmark}\)

注意到出现次数只有 \(\mathcal O(\sqrt n)\) 个。

枚举一个 \(x\) 和出现次数 \(k\)，对于这个 \(k\) 从大到小遍历元素，找到第一个没有 ban 掉的，均摊复杂度正确。

复杂度有显然的上界 \(\mathcal O(n \sqrt n)\)，也许可以分析的更紧，但是这个已经能过了。

F. Towers \(\color{red}{\times}\)

毫无头 zhu，怎么回事呢。

考虑以 \(h_i\) 最大的点为根，则除根外每个点子树内只需要选择一个 \(e \ge h\) 的点 \(x\)，因为必然有一条路径从 \(x\) 出发穿过这个点到达另一个根下的点。

那么贪心的，找到每个子树内 \(e\) 最大的并填到 \(h\)，对于根选两个即可。复杂度线性。

G. Birthday \(\color{red}{\times}\)

Key ob.

• 操作结束后，每个数字都会变成 \(2^{\lceil \log_2 n\rceil}\)。
  考虑最终变成的数 \(x\)，假设其含有任何奇素数因子 \(p\)。注意到 \(x,y\) 如果满足 \(x \not \equiv 0 \pmod p\) 或 \(y \not \equiv 0 \pmod p\)，那么操作一次后 \(x,y\) 一定不可能全 \(0\)。

注意只要存在一个 \(0\)，我们就可以把任意 \(x\) 通过 \((0,x),(x,x)\) 将 \(x\) 翻倍同时保留 \(0\)。那么，我们先将所有数字变到 \(2\) 的整数次幂。

设计 \(f(n)\) 表示构造将 \(1 \sim n\) 变成 \(2\) 的整数次幂。

• 如果 \(n\) 是 \(2\) 的整数次幂，那么直接调用 \(f(n-1)\)。
• 如果 \(n = 0\)，推出。
• 否则，找到 \(p = 2^{\lfloor \log_2 n \rfloor}\)。操作 \((p-1,p+1),(p-2,p+2),\ldots,(2p-n,n)\)，注意到以上两两配对，会形成若干个 \(2p\) 和 \(2,4,6,\ldots\)，同时有 \(1 \sim 2p-n-1\) 未操作。调用 \(f(2p-n-1)\) 和 \(f(n-p)\)，注意把 \(f(n-p)\) 乘 \(2\)。

容易发现产生了很多 \(2\) 的次幂，因此一定有一个 \(2^r\) 出现了两次，操作 \((2^r,2^r)\) 即可得到 \(0\)，再把每个数字乘 \(2\) 乘到答案即可。

CF1500（Div.1）

A. Going Home \(\color{green}{\checkmark}\)

由抽屉原理，当 \(n \ge 10000\) 时一定有解，故把 \(n\) 对 \(10000\) 取 \(\min\) 后跑 \(\mathcal O(n^2)\) 暴力即可。

B. Two chandeliers \(\color{red}{(\checkmark)}\)

注意到两个数组以 \(\operatorname{lcm}(n,m)\) 为周期。数组元素互不相同，意味着一个周期内 \(a_i\) 最多匹配一次。

二分答案 \(l\)，拆成整周期和散的计算，\(a_i\) 需要几次才能匹配是在求同余方程 \(i + xn \equiv ps_{a_i} \pmod m\) 的解。对于散周期，如果这个解小于 \(a\) 的出现次数即计入答案。

由于 \(n\) 始终不变，可以提前预处理同余方程答案。

注意：std::lcm(int a,int b) 会返回 int 而不是 long long！

C. Matrix Sorting \(\color{red}{\times}\)

倒序看操作序列 \(a_1,\ldots,a_k\)，实际上是先按照 \(a_k\) 排序，对于 \(a_k\) 相同的按 \(a_{k-1}\) 排，依次类推。这是一个 \(k\) 关键字的排序过程。

首先如果 \(b\) 的行集合和 \(a\) 的行集合不相等肯定直接无解，先把它判掉。考虑先找到 \(b\) 中一个递增的列，然后再找到一列满足上一次排序后相等的段也递增，一直到找不到这样的列。找不到后，显然需要满足剩下的连续段里编号递增。

如果有多个递增的列，我们可以任选，因为每次选择的区间是包含关系，先选择小区间后小区间内大区间仍然合法。

每次暴力找这样的列是 \(\mathcal O(n^3)\) 的，但是我们可以 bitset 优化，即对每一行开 bitset，每一行把这一行大于等于上一行的列记录下来，每次与上这些行的 bitset 即可除掉一个 \(w\)。

D. Tiles for Bathroom \(\color{red}{\times}\)

考虑按照 CF1753F 的套路枚举对角线，问题是这道题每次暴力扫 \(\mathcal O(n^3)\) 是过不了的。

注意到 \(q \le 10\)，考虑让复杂度带 \(q\)。我们只需要找出颜色不同的切比雪夫距离前 \(q+1\) 大的点即可确定以它为右下角正方形大小，可以根据 \((i-1,j-1),(i-1,j),(i,j-1)\) 快速递推。

E. Subset Trick \(\color{red}{\times}\)

首先有显然的 \(\mathcal O(nq)\) 做法。

注意到我们要求的是一堆区间 \([\max(r_{i-1},l_i),r_i)\) 的并，考虑从这些区间的形态上入手观察有没有什么好的性质。

发现 \(l\) 的增速在增大，而 \(r\) 的增速在减小，因此 \(l_{i+1}\) 和 \(r_i\) 的大小关系必然最多分为三段：左右的有 \(r_i < l_{i+1}\)，而中间的有 \(r_i \ge l_{i+1}\)，找出它们后答案很好计算。

CF1495（Div.1）

A. Diamond Miner \(\color{green}{\checkmark}\)

显然符号没有用，直接取绝对值。然后猜一下排序是最优的，prove by AC。

B. Let's Go Hiking \(\color{red}{(\checkmark)}\)

Daniel 的策略比较有限：对冲和忽略对方。首先 QS 如果只能往一边走，那么 DN 直接堵死，QS 输。那么 QS 一定要选择可以往两边走的。

前一种是选择一个和 Qingshan 位置奇偶性不同的，逼迫 Qingshan 走另一边；后一种是直接选择一个和 QS 不交的区间走。枚举 \(x\) 都判断一下即可。

好像有结论是答案不超过 \(1\)，不过无所谓了，这个做法不太依赖。

C. Garden of the Sun \(\color{red}{(\checkmark)}\)

做过 Yin Yang 的话这个题是不是直接秒啊！

考虑在列 \(\bmod 3 = 0\) 的地方涂一条竖线，竖线之间会隔两列，则任意一个方块会连在一条竖线上。

竖线的连通是容易的，只需要在竖线间找一个已经有一个 X 的行连起来即可，没有的话随便选一行。

特判最后剩两列的情况。

D. BFS Trees \(\color{red}{\times}\)

考虑以 \(1\) 为根的最短路树个数怎么求：只需要对每个点可能的父亲数量计数后乘起来。

首先有个比较显然的性质是，如果 \(s \to t\) 有超过一条最短路答案一定是 \(0\)。（为啥我没发现？？？）

我们把 \((s,t)\) 的链看作树根，则对于边 \((u,v)\) 要有 \(u\) 是 \(v\) 的父亲需要同时满足 \(d_{s,u} + 1 = d_{s,v},d_{t,u} + 1 = d_{t,v}\)，直接数就行了，，，

F. Squares \(\color{red}{\times}\)

首先注意到这是一个 dag 且边都有 \(i<j\)，因此答案即为 \(s\) 中相邻点对的最短路的和。

注意到最短路的总对数是 \(\mathcal O(q)\) 级别的，我们可以离线全都求出来。

注意到所有 \([i,b_i)\) 的区间要么包含要么不交，因此考虑倒序扫描 \(l\)。维护 \(r\) 的最短路，如果 \(b_i\) 短于最短路，则给 \([b_i,n+1]\) 的最短路减去差值即可。FWT 维护之。

CF1477（Div.1）

A. Nezzar and Board \(\color{green}{\checkmark}\)

• ob1：所有最终生成的数字，可以表示为 \(\sum p_ia_i - \sum q_ia_i\) 的形式，且 \(\sum p_i = \sum q_i + 1\)。
• ob2：我们可以两两配对，即，任选若干对数字的差加起来，然后最后加上一个 \(a_i\)。
• ob3：所有 \(a_i - a_j\) 的 \(\gcd\) 等于排序后两两差的 \(\gcd\)。

B. Nezzar and Binary String \(\color{green}{\checkmark}\)

倒序做就结束了。

C. Nezzar and Nice Beatmap \(\color{red}{\times}\)

考虑人类智慧：每次选离 \(A\) 最远的点 \(B\) 连边，此时所有其它点 \(C\) 都在以 \(AB\) 为半径的圆内，这个角显然小于 \(90\) 度。

D. Nezzar and Hidden Permutations \(\color{red}{\times}\)

首先注意到 \(n - 1\) 度点没有用，在所有拓扑序里它的位置都相同。

人类智慧的，考虑图的补图。补图的每一个连通块大小至少为 \(2\)，且连通块间是独立的。

如果补图是菊花，可以依次赋上 \(1,2,3,4,5\) 和 \(5,1,2,3,4\)。

否则，我们找出一棵生成树并把这棵树划分为若干菊花。

CF1458（Div.1）

A. Row GCD \(\color{green}{\checkmark}\)

经典套路，差分后求出 \(\gcd(a_i - a_{i-1})\)，然后每组询问和 \(a_1 + b_i\) 取 \(\gcd\)。

B. Glass Half Spilled \(\color{red}{(\checkmark)}\)

最优解肯定不会在没有选中的杯子上相互转移，直接背包即可。抄了 t 宝的代码。

C. Latin Square \(\color{red}{\times}\)

观察 I 和 C 操作有什么性质：把 \((i,p_i)\) 看作平面上一个点，将排列变为逆排列相当于交换 \(i,p_i\)。

那么把 \((i,j,a_{i,j})\) 看作平面上的点，维护三维的增量即可。

D. Flip and Reverse \(\color{red}{\times}\)

人类智慧：将 \(0\) 看作 \(-1\)，求出前缀和 \(s_i\)，把 \(s_i \to s_{i+1}\) 连边，则一次操作等价于翻转一个环。

观察到所有欧拉路径都可以通过翻转操作拼凑出，因此直接求字典序最小的欧拉路径即可。由于边只有 \((i,i+1)\)，这个是容易求的。

CF1383（Div.1）

A. String Transformation 1 \(\color{green}{\checkmark}\)

按字符从小到大贪心即可。

B. GameGame \(\color{green}{\checkmark}\)

注意到如果某一位出现了偶数次，那么不论怎么划分其在两个子集里贡献都相同；反之如果出现了奇数次，其在两边的出现次数一定不同。那我们只需要关心最高出现了奇数次的位。

现在问题变成这样：有两堆石子 A,B，每个人每一次可以从任意一个石子堆中取走一个石子，最终取走了奇数个 B 石子的获胜。

考虑如果 \(\dfrac{b-1}{2} \bmod 2 = 0\)，那么先手可以先取走一个 B，然后和后手下模仿棋，这样不论怎样剩下的 B 石子都会被平分，先手必胜。

反之，如果先手先取 B，那么后手也来下模仿棋，先手会输掉。这时候需要 A 石子堆来交换先后手，判断 A 堆石子数量的奇偶性即可。

C. String Transformation 1 \(\color{red}{\times}\)

什么神秘数竞题，不知道有什么意义。垃圾。出题人你妈死了。

考虑建一张图，\(a_i \to b_i\) 连边。设这张图有 \(c\) 个连通块，且最大导出 DAG 的点数是 \(k\)，直接给出结论：答案是 \(2n - k - c\)。

• 充分性：构造证明。将图顶点重标号，使得 DAG 部分按拓扑序标号为 \(1\sim k\)。
  • 首先顺次操作 \((k+1,k+2),\ldots,(n-1,n),(n,1)\)，这样所有 \(k+1 \sim n\) 的元素都聚集到了 \(1\)。
  • 然后顺次操作 \((1,2),(2,3),\ldots,(n-1,n)\)。
  • 这样操作完只有 \(\forall i,j \in [1,k],i > j\) 的点不可达，而由于这是一个 DAG 的拓扑序，故这样的边不存在。
• 必要性：我们证明另外一个结论：如果存在一种操作数为 \(e\) 的方案，则原图一定存在大小至少为 \(2n-e-c\) 的导出 DAG。依次考虑 DAG 中的每一条边 \((u,v)\)，维护一个点集 \(S\)，初始为全集。
  • 如果这条边连接的两点不在同一个若连通块，则直接连接。
  • 否则，如果 \(v \in S\)，将 \(v\) 从 \(S\) 中删去。
  • 考虑这样操作完后 \(S\) 的形态：如果 \(u,v \in S\) 且存在 \(u \to v \to u\) 的环，那么在 \(v \to u\) 这条路径加入时，\(u,v\) 已经弱联通，\(v\) 会被删去，故 \(S\) 是一个 DAG。
  • 操作 \(1\) 有恰好 \(n - c\) 个，故操作 \(2\) 只会有 \(e-(n-c)\) 个，故 \(|S| \ge n-(e-n+c) = 2n-e-c\)。
    证毕。

D. Rearrange \(\color{red}{\times}\)

很困难的题，我的思路是先让行满足要求再去调整列，但是很久都没有什么进展。

注意到题目限制了 \(\max\)，那我们考虑直接降序填入所有元素，这样如果填了新的一行或者一列，它一定是 \(\max\)；否则它一定不是 \(\max\)。

如果数字 \(i\) 是 \(\max\)，那我们新开一行/一列，然后我们就需要将数字逆序填入这一行 / 一列的其他位置。可以直接将这些位置用队列维护。

一个最大值的左上一定是升序，因为我们的队列是按照这个顺序填入的；右下也一定合法，因为我们是降序填入的。做完了。

CF2023（Div.1）

Guess Forces。

A. Concatenation of Arrays \(\color{green}{\checkmark}\)

首先不难想到对于 \(i,j\)，如果 \(i\) 在 \(j\) 前面造成的逆序对比较少就让 \(i\) 在前面，否则让 \(j\) 在前面。但是这样做会 wa on test 3，原因是逆序对相等时会出问题。

正确的做法有很多，可以先 \(\max\) 后 \(\min\)、先 \(\min\) 后 \(\max\) 或者直接比较和，都可以调整证明（？

B. Skipping \(\color{green}{\checkmark}\)

观察到如果已经走到了位置 \(i\)，那么所有 \(i\) 之前的位置都会被计入答案。那么线段树优化 DP 即可。

还有一种最短路做法，仍然是基于上述观察，设 \(f_i\) 表示走到 \(i\) 的最小 skip 代价，连边 \((i,i-1,0),(i,b_i,a_i)\)，答案是到 \(n\) 的最短路。

C. C+K+S \(\color{green}{\checkmark}\)

• 观察 \(1\)：一张合法的图一定是一张 \(k\) 分图，且颜色 \(i\) 只和颜色 \((i+1) \bmod k\) 之间有边。
• 观察 \(2\)：从第一张图连向第二张图的边一定都是这个形式，即需要存在一种颜色的对应关系 \(i \to p\) 有边，\(i + 1 \to p + 1\) 有边，\(p \to i + 2\) 有边。

综上可以哈希判断。

D. Many Games \(\color{red}{(\checkmark)}\)

显然有一个暴力 DP 做法，但是复杂度显然爆炸。

注意到这个问题其实非常困难，考虑进行一些剪枝：

• 概率如果太低显然期望会很小，因此当概率 \(\le 10^{-4}\) 时直接退出。
• 最终的 \(\sum w\) 直觉上不会超过 \(2 \cdot 10^5\)。
• 如果一个概率有很多元素，我们只选取前面的一点点。具体的，当乘积小于等于 \(10^{-4}\) 时直接退出。

然后就直接 AC 啦！拜拜程序！

E. Tree of Life \(\color{red}{\times}\)

神秘结论题。

链覆盖的过程如果从下向上合并，在每个点做的决策会很困难。

考虑这样一种策略：首先覆盖掉每个点的 \(\dfrac{s(s-1)}{2}\) 对儿子之间的边，然后向每个儿子下传一条长度为 \(s-1\) 的链。这样的问题是，会存在一些无法被上面传下来覆盖的链，这时候我们希望其两两匹配。

这时候题解断言：选择度数最大的根，一定存在一种合法的匹配方案。咋证明，不会。