CF 做题笔记

\(\texttt{Ac*\_**bin}\)：做过的题要写题解！

\(\texttt{t**l}\)：要制定训练计划！

\(\texttt{Le0**an}\)：我写了三篇做题笔记了！

于是就有了这篇。

设有两段区间 \(a,b\)，我们希望 \(a\) 成为最大值，\(b\) 成为最小值，那么我们一定会问只有 \(a\) 会的问题；问 \(a,b\) 都会/都不会的问题没有意义。因此，答案是 \(2(|a|-|a \cap b|)\)。我们枚举 \(a\)，考虑什么样的 \(b\) 是有意义的。分类讨论：

  • \(a\) 和 \(b\) 不交

显然答案是 \(2|a|\)。

  • \(a\) 和 \(b\) 交但没有包含

我们贪心的选择右端点最靠左的区间 和 左端点最靠右的区间，进行比较。

  • \(a\) 和 \(b\) 包含

此时答案为 \(2(|a| - |b|)\)。发现我们只需要找长度最小的区间。如果这个区间并没有包含，那么显然已经考虑在情况 \(1,2\) 中，而这种情况比包含任意一个长度大于等于这个长度的区间都优。如果包含，选择这个即可。

时间复杂度 \(\mathcal O(n)\)。评测记录。

策略是前半部分变成负的，后半部分变成正的。考虑在正负两种情况下你需要操作一次的条件是什么。枚举分界点，动态更新答案。时间复杂度 \(\mathcal O(n)\)。评测记录。

显然的是，一边攒魔法一边打怪物没有任何意义，我们的策略是先攒够魔法再一次性暴击怪物。枚举用多少“水系咒语”打怪物，剩余的用“火系咒语”。但是你要保证那个值可以恰好打死若干只怪物，不能出现打不死怪物的情况。

那么我们背包一下，时间复杂度 \(\mathcal O(n^2s)\)，卡着能过。要想卡个常的话可以 bitset。评测记录。

状压 + 最短路裸题，几乎是板子就不说了。时间复杂度 \(\mathcal O(2^nm \log (2^nm))\)。

说句闲话：这题想了半小时，写了半小时，拍了半小时，最后假了。

贪心。变小只改最后一个，变大只改第一个，感性证明。时间复杂度 \(\mathcal O((|\Sigma|)^2n)\)，本题 \(|\Sigma| = 5\)。评测记录。

首先 \(n \bmod 3 \ne 0\) 肯定无解；然后随便找个点当根 dfs 一遍，\(f_u\) 表示 \(u\) 为根的子树里的多余点的剩余量，直接搜即可。评测记录。

贪心。答案的下界是 \(\lceil \dfrac{\sum a_i}{n} \rceil\)，考虑怎么达到。我们的策略是拿若干组狂打一只怪，打死再打下一只。对怪物生命做前缀和，设 \(s_i = (\sum\limits_{i=1}^n a_i) \bmod n\)，\(s_n\) 是无意义的因为最后多余的组都会暴击最后一只怪，那么令 \(s_m = n\)。排序后，令 \(c_i = s_i-s_{i-1}\)，则 \(c_i\) 就是第 \(i\) 个组的人数。显然 \(\sum c_i = n\)，接下来考虑它的意义。如果我们 \(m\) 个组打了一轮，则怪物生命减少 \(n\)。到了最后，怪物的生命一定是 \(a_i \bmod n\)。而我们顺序杀死每一只怪物，则相当于打死一只怪物消耗的人数是那个对应的前缀和模 \(n\)，而这个前缀除了 \(i=m\) 时都在 \(c\) 中存在，即不会造成浪费。会浪费的只有最后一次，答案的下界总可以达到。

构造方案时，直接根据上面的方法模拟即可。评测记录。

水水水水水。

先把式子拆成 最大值的和减去最小值的和，然后点权转边权，就成了 ABC214D。要求最大值的和，我们将边从小到大排序，并查集维护，每条边的贡献是 \(w \times siz_u \times siz_v\)。最小值同理。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

我们先任意求出一棵最小生成树，考虑一条边 \((u,v)\) 在最小生成树上的条件。

  • 它是树边。那么不能存在一条边 \((x,y)\)，使得断开 \((u,v)\) 连接 \((x,y)\) 后仍然是树形，且 \(w_{x,y} \le w_{u,v}\)。
  • 它是非树边。只需要在 \((u,v)\) 的路径上存在一条边 \((x,y)\) 使得 \(w_{x,y} > w_{u,v}\)。

第二种情况是好做的，只需要维护路径上的最大值。对于第一种情况，我们反过来考虑，遍历每一条非树边，把路径上树边的边权和这条边边权 \(-1\) 取 \(\min\)。树剖即可。时间复杂度 \(\mathcal O(n \log^2 n)\)。评测记录。

树剖优化交互过程的好题。

naive 的思路是从 \(1\) 一直执行询问 \(2\) 直到找到，可惜询问次数不够。我们每次跳深度和 \(x\) 的相同的对应重儿子，然后通过问这个儿子和 \(x\) 的距离得到他们的 LCA，再进行询问 \(2\)。这样询问次数是正确的，应用了路径上轻边不超过 \(\log\) 条的树剖经典结论。找 lca 时需要 k 级祖先，我直接写了倍增，其实有更优秀的实现方法。评测记录。

注意最后的答案是与起来的，也就是说你希望一位是 \(1\) 必须所有 \(c_i\) 都是 \(1\)。拆位贪心考虑。\(a_i\) 和 \(b_i\) 是异或起来的，因此如果你希望 \(c_i\) 在这一位上是 \(1\)，必须每一个 \(a_i,b_i\) 在这一位上都不同。

我们发现高位的选择和低位是有关系的，不能直接扫一遍。我们有式子：\((a_i \operatorname{and} ans) \oplus (b_i \operatorname{and} ans) = ans\)，也就必须有按位取反后的 \(b_i \operatorname{and} ans\) 和 \(a_i \operatorname{and} ans\) 相等。map 维护即可。时间复杂度 \(\mathcal O(n \log n \log a_i)\)。评测记录。

注意到所有 距离自己节点距离的最大值 \(\ge k\) 的点构成一个连通块，其余点每个点单独构成连通块，考虑如何维护。题解告诉我们一个经典结论：距离每个点最远的点一定是树的直径的一端。于是搜出树的直径后得到每个点的最远距离，后缀和一下即可。时间复杂度 \(\mathcal O(n)\)。评测记录。

显然答案一定形如前缀一段 \(0\) 拼上后缀一段 \(1\)。我们的交换肯定会交换前面的 \(1\) 和后面的 \(0\)。因为 \(10^{12}\) 次方很大，我们肯定要让操作次数最小。考虑一个结论：交换操作只会发生一次，否则可以直接删除那个 \(1\)。统计出前缀 \(1\) 和后缀 \(0\) 的数量，枚举 删除前缀 \(1\) 和 删除后缀 \(0\) 的分界点，若删除后缀 \(0\) 部分的第一个 \(1\) 后面恰好是 \(0\)，那么答案 \(-1\)。时间复杂度 \(\mathcal O(n)\)。
评测记录。

水水水水水，不知道为什么是蓝的。

发现一次修改操作只会影响三个节点的信息：\(fa_u,u,son_u\)，画个图研究一下它们的变化。开个 set 维护每个点的所有儿子信息，取出 set 的第一个即为重儿子，然后直接操作即可。时间复杂度 \(\mathcal O(n + m \log n)\)。评测记录。

边数太大，无法承受直接建图的复杂度。我们对每个质因子建立虚点，向所有它的倍数连无向边，最后将答案除以 \(2\)。质因子的倍数有限，最终边的数量是 \(\mathcal O(n \log a_i)\) 级别。边权都是 \(1\)，可以 bfs。那么时间复杂度 \(\mathcal O(n \log a_i)\)。评测记录。

分奇偶构造。

\(n\) 为偶数时，直接输出以 \(n\) 为中心的“回文串”，例如 \(n=6\) 时，构造 \([3,4,5,7,8,9]\)。显然 \(\sum a = n^2,\max - \min = n\)。

\(n\) 为奇数时，仍然构造“回文串”。当 \(n=7\) 时，构造 \([4,5,6,7,8,9,10]\)。显然的，此时 \(\sum a = n^2\) 但 \(\max - \min = n-1\)。我们进行两步处理，把 \(\sum a \to (n+1)^2,\max - \min \to n + 1\)。

  1. 步骤一：\(a_i \gets a_i + 2\)。此时 \(\max - \min\) 不变，和增加 \(2n\)。

  2. 步骤二：\(a_1 \gets a_1 - 1,a_n \gets a_n+1,a_{n-1} \gets a_{n-1}+1\)。此时 \(\max - \min\) 加 \(2\)，和加 \(1\)。

至此完成构造。时间复杂度 \(\mathcal O(n)\)。评测记录。

二分答案，考虑如何 check。

从根到儿子贪心，找到第一个深度 \(> mid\) 的点断开是显然错误的，考虑深度为 \(mid\) 的点下挂了很多儿子，此时直接在 \(mid\) 处断最优。

我们从下向上贪心，如果该点深度不满足要求，那么断开其 \(mid-1\) 级祖先。倍增维护树上 \(k\) 级祖先，线段树 + dfn 序判断点是否已经断开，时间复杂度 \(\mathcal O(n \log^2 n)\)。

题解各种好写还少只 $\log $ 的做法，是我小丑了。评测记录。

拆位，从高到低每一位贪心的选 \(0\)。我们要选的边，必须满足已经考虑的位置该权值是答案的子集；然后用并查集判断满足上面条件的边权这一位是 \(0\) 的边是否连通。时间复杂度 \(\mathcal O((n+m) \log n \log w_i)\)。评测记录。

很无聊的一道题，思维难度 \(0\)，细节一车。考虑最后一位变化会包含所有位数，那么只需要考虑前面的位数的影响即可。map 随便搞一搞就好。

怎么看怎么水，但是各种细节搞得我 1h 才过。

首先你发现你不论怎么操作区间异或和不会变，所以如果异或和不是 \(0\) 直接 \(-1\)。然后分区间长度奇偶讨论，奇数时候是平凡的，此处不再赘述。考虑几种偶数情况，以下记 \(k = r-l+1\)。

  • \(k=2\)。此时你不能操作，如果 \(a_l=a_r=0\) 那么答案 \(0\)，否则 \(-1\)。

  • 区间全 \(0\)。答案显然是 \(0\)。

  • \(a_l = 0\) 或 \(a_r = 0\)。答案显然是 \(1\)。

  • 存在一个点 \(i(l < i<r-1)\) 满足 \((i-l+1) \bmod 2 = 1\) 且 \(\oplus_{j=l}^i=0\)。此时答案为 \(2\)。特别注意此时 \(i \ne r- 1\)。

对于情况 4，我们使用 vector 记录所有奇数位/偶数位前缀和对应的下标，运用差分查询。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

无论是贪心还是 dp 都是一道好题，限于篇幅这里只写贪心做法。

首先要得出的结论是，若点 \(u\) 的度数是 \(d_u\)，且它要被覆盖 \(k\) 次，那么它的每个儿子至少覆盖 \(\lfloor \dfrac{k}{d_u} \rfloor\) 次，至多覆盖 \(\lceil \dfrac{k}{d_u} \rceil\) 次。证明显然。

我们对于每个儿子保留其子树内点权和最大的链向上继承，对于每个点维护一个堆，取其前 \(k \bmod d_u\) 大链，然后将剩余的最大向上继承。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

感觉这题黄题差不多了。

每次会从 \(100\) 个数字里随便选一个，还只能问两次，值域 \(2^{14}-1\)，其实提示的相当明显了。第一次问确保所有数字前 \(7\) 位都是 \(0\)，第二次确保所有数字后 \(7\) 位都是 \(0\)，两次结果拼起来就好。评测记录。

好水，建议降橙。

所有点在一个环上，我们问一次 \((a,b)\)，问一次 \((b,a)\)，如果答案不同，那么两个答案加起来就是环的大小。交互库保证随机，那么问 \(25\) 组问不到的概率只有 \(2^{-25} \le 0.000003\%\)，只有 \(50\) 组数据，应该不会有人运气这么差吧 qwq。评测记录。

以下用 黑色 表示坏人，白色 表示好人。

我们如果知道一个黑色和白色的位置，可以简单通过 \(n-2\) 次询问得到所有位置的颜色。那么考虑如何找到这两个位置，\(\dfrac{n}{3} < k < \dfrac{2n}{3}\) 这个奇怪的条件很关键。我们顺次问过 \((1,2,3),(2,3,4),(3,4,5),\ldots,(n,1,2)\) 这 \(n\) 个对，一定存在两个对黑白数量大小关系不同。找到这两个对，立即可以得到一黑一白，然后就做完了。评测记录。

延续上面 easy version 的思路，先找到两个位置 \(l,r\) 满足 \(l\) 是黑色，\(r\) 是白色。我们把序列分成 \(\dfrac{n}{3}\) 块，每次问 \((i,i+1,i+2)\)，那么显然存在相邻的两块数量大小关系不同。设这两块左端点是 \(p,q(p < q)\)，询问 \((p+1,p+2,p+3),(p+2,p+3,p+4)\)，就能得到 \(l,r\) 的值，这里和 D1 类似。然后拿着 \(l,r\) 枚举每一块，假设这一块大小关系是 \(0\)。（\(1\) 同理）设 \(i\) 是这一块的左端点，我们询问 \((i,i+1,r)\)，\((i+1,i+2,r)\)，一定可以唯一确定 \(i,i+1,i+2\) 的黑白。当然进行这次询问的条件是 \(i \ne p,i \ne q\)。如果 \(i=p\) 或 \(i=q\)，用 D1 的方法暴力枚举即可。总的询问次数 \(n+2\)。代码实现稍微复杂，写的时候想清楚。评测记录。

根据 \(\operatorname{MAD}\) 运算的性质，易推出以下结论：

  • 如果最大值出现了 \(\ge 3\) 次，那么断开所有边答案都是这个值。感性理解，虽然严格证明也不难。

  • 否则，只有断开其两次出现的点 \(u,v\) 的链上的边，才会影响答案。

我们考虑如何计算这条链上的答案。钦定最大值一次出现的位置 \(v\) 为树根 dfs，方便之后处理。我们从链的另一端 \(u\) 向上跳，维护两个 set 和两个 map 分别表示下面的子树和除去这个子树外的部分。每次遍历到点 \(u\)，访问其子树内没有被访问过的地方，让下面子树的 map 对应位置 \(-1\)，同时更改 set 的值。然后，记录下答案为两个 set 的 \(\max\)，再向上跳即可。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

容易发现除了第一个传送点，其他点代价都是 \(a_i+\min(i,n-i+1)\)。贪心的考虑，将所有点代价从小到达排序。枚举第一个传送点，树状数组或线段树维护代价，二分查找。写代码的时候降智了，把前缀和又前缀和了一遍，然后写了区间改区间查的线段树。。。时间复杂度 \(\mathcal O(n \log^2 n)\)。评测记录。

感觉这题可以紫啊，不知道咋就降蓝了。

你发现 \(\operatorname{mex} = i\) 的数量就是 \([0,i-1]\) 都出现的方案数减去 \([0,i]\) 都出现的方案数。 然后假设我们有一条维护好的链 \((u,v)\)，新加入点 \(x\)：

  • 若 \(x\) 在这条链上，则什么也不会发生。

  • 若 \(x\) 在这条链的“延长链”上，则链扩展。

  • 否则，答案为 \(0\)。

当你知道端点 \(u,v\) 时，如果 \(u \ne 1,v \ne 1\)，那么显然方案是 \(siz_u \times siz_v\)。否则，假设 \(u=1\)，那么方案数是 \(siz_u \times(siz_u - siz_r)\)，其中 \(r\) 是 \(u \to v\) 路径上的第二个点。维护一下即可，有一些实现细节。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

距离为 \(1\) 即与链上某个点相邻，而不论是相邻还是直接经过都会经过这个点的父亲。把关键点转化为父亲，按深度排序，判断后面的点在不在前面的子树里即可。时间复杂度 \(\mathcal O(n+k\log k)\)。评测记录。

二分 + 数位 dp + 状压，还是相当板子的，关键是要能想到用二分转化为数位 dp 问题。注意不要重复 memset，会 T 飞。评测记录。

玄学题，暴力删 \(0\) 复杂度就是对的，模拟就好。证明 \(\to\) link。评测记录。

由于边权互不相同，最小生成树唯一。对于每个点，如果它的答案要正确，我们要保证以它为根时，所有非树边都是返祖边，因为 dfs 遍历无向图不会出现横叉边。我们对于每一条非树边，给它连接的两端点的子树内点权 \(+1\)，显然最终点权为 \(m-n+1\) 的点是合法点。树上差分维护，时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

\(a\) 的长度只有 \(n-1\) 时，可以直接构造前缀和。类似的，我们先枚举位置 \(j\)，将 \(b\) 构造为 \(a\) 的除了 \(j\) 的前缀和，然后判断是否存在若干元素的和或差能够拼出 \(a_j\)。时间复杂度 \(\mathcal O(n4^n)\)。评测记录。

\(a \operatorname{and} b + a \operatorname{or} b = a+b\)。然后依次问过 \(a_1+a_2,a_1+a_3,\ldots\)，最后问 \(a_2+a_3\)，解个三元一次方程组，手玩即可。当然你也可以高斯消元。评测记录。

水水树剖。

先拆一下题目中的式子，原式即：

\[\dfrac{b_x^2\sum\limits_{i=1}^ns_i^2-2cb_x\sum\limits_{i=1}^ns_i+nc^2}{n} \]

我们要做的是维护子树颜色出现次数的平方和和和。动态开点线段树 + 树剖即可，每次修改时，改 \(1 \sim u\) 的链。时空复杂度均为 \(\mathcal O(n \log^2 n)\)（\(n,m\) 同阶）。评测记录。

考虑 Floyd 的过程，发现如果存在一个点 \(u\)，满足它不和任意一个关键点相连，那么这个 Floyd 必然是错的。然后剩下的点随便连，看是否能连够 \(m\) 条边判有无解。注意 \(u\) 要选标记点，这样连边上线可以 \(+1\)。然后注意连边时，务必保证图连通，务必保证无重边自环。评测记录。

由于每个点双都是完全子图，手模样例后发现最短路就是圆方树上距离除以 \(2\)，直接做。时间复杂度 \(\mathcal O(n+m+q \log n)\)。评测记录。

注意到奇怪的限制：\(m-n \le 20\)，启发我们建出最小生成树后枚举非树边。对每个非树边的两个端点为源点跑最短路，查询时，每次枚举这些点做中转点，对 \(ans\) 取 \(\min\)。不要忘记和原树上距离取 \(\min\)。时间复杂度 \(\mathcal O(km \log m + kq \log n)\)，其中 \(k = 42\)。评测记录。

把这题想简单了，一直一维 dp 推式子，寄寄。

设 \(f_{i,j}\) 表示处理前 \(i\) 个程序，上一次在 CPU 2 运行的程序是 \(j\) 的最小代价。显然这种情况下上一次在 CPU 1 运行的程序是 \(a_{i-1}\)。我们先考虑，如果上一个程序在 CPU 1 运行，此时 \(j\) 值不变，\(f_{i,j} = f_{i-1,j} + c_i\)，\(c_i\) 是程序 \(i\) 的代价。如果程序 \(i\) 在 CPU 2 上运行，我们交换两个 CPU，得到 \(j = a_{i-1}\)，\(f_{i,a_{i-1}} = f_{i-1,j} + c_i\)。时间复杂度 \(\mathcal O(nk)\)。评测记录。

这题没自己想出来真的是降智了 /kel

考虑暴力 dp，\(\mathcal O(n^2)\) 显然过不了，但是值域很小。我们反向思考，维护答案桶，对应下标记录异或值对应的最小 \(a_i\)，每次转移枚举之前的异或和 \(j\) 判断是否合法。时间复杂度 \(\mathcal O(nV)\)，\(V=100\)。评测记录。

  • CF1891D Suspicious logarithms \(^*1900\)

一个显然的结论是：设 \(l=2^k,r = 2^{k+1}-1\)，那么 \(g(r) - g(l) \le 1\)。证明非常简单：因为 \(f(l)=f(r),g(l) \ge 2\)，而 \(r < 2l\)，对于固定的底数 \(y(y \ge 2)\) 区间内最多存在一个 \(y\) 的正整数次幂 \(y^k\)，那么 \(g(l) \to g(r)\) 的增量就显然不超过 \(1\) 了。

我们枚举 \(i=\log_2(x)\)，记输入的 \(l,r\) 为 \(L,R\)，我们首先计算 \(l=\max(L,2^i),r = \min(R,2^{i+1}-1)\)，并计算 \(g(l) = \log_{i}l\)。然后计算 \(p = i^{g(l)+1}\)，判断是否在该区间内。如果在，那么 \([l,p)\) 的答案为 \(g(l)\)，\([p,r]\) 的答案为 \(g(l)+1\)。时间复杂度 \(\mathcal O(q \log^2V)\)。评测记录。

水题。考虑固定左端点，不同的 \(\gcd\) 数量是 \(\log\) 级别的。二分这 \(\log\) 个端点，st 表维护区间 \(\gcd\) 即可。时间复杂度不会高于 \(\mathcal O(n \log^3 n)\)。评测记录。

  • CF1891F A Growing Tree \(^*2000\)

因为树形固定且没有删除操作，我们考虑离线处理。先把整棵树建出来，然后要做的就是给 \(u\) 的子树 \(+x\)。但是，因为加法时不一定所有子树内的点都建了出来，所以我们不能简单的给 dfn 序区间做加法。

我们给每个点增加一个属性 \(t_i\) 表示点 \(i\) 是什么时候出现的，那么本质上，一次操作 \((u,x)\) 等价于给满足 \(dfn_u \le dfn_y \le dfn_u+siz_u-1,t_y \le t_u\) 的点 \(y\) 做 \(+x\)。你发现这是一个二维区间加法，把它差分一下，变成了二维平面内单点修改区间求和。树状数组离线二维数点即可。时间复杂度 \(\mathcal O(q \log q)\)。评测记录。

太水了，建议降绿。容易发现答案单调，二分一下，AC 了。时间复杂度 \(\mathcal O(\log^2 n)\)。评测记录。

因为只有三个点，我们可以暴力重排计算答案，问题转化为对于确定的 \(a,b,c\) 计算答案。好像有很多巧妙做法，这里给出一种理解简单的分类讨论做法：

  • 情况一：\(a,b\) 都在 \(c\) 的子树内。

此时答案显然为 \(dep_c - dep_{\operatorname{lca}(a,b)}+1\)。

  • 情况二：\(a,b\) 一个在 \(c\) 的子树内，另一个不在。

此时答案显然为 \(1\)。

  • 情况三：\(a,b\) 都在 \(c\) 的子树外。

这种情况还需要继续分类：

  1. \(\operatorname{lca}(a,c) = \operatorname{lca}(b,c)\)。

画图理解一下，发现这种情况 \(a,b\) 在 \(c\) 子树外的同一棵子树，答案是 \(\operatorname{dis}(c,\operatorname{lca}(a,b))\)。

  1. \(\operatorname{lca}(a,c) \ne \operatorname{lca}(b,c)\)。

此时两条路径一定只在 \(1 \to c\) 的链上有交，那么答案应该是两个 \(\operatorname{lca}\) 之间较深的和 \(c\) 的距离。

到这里代码就很好写了，分析一下复杂度，瓶颈在求 \(\operatorname{lca}\)。这里采用朴素的倍增实现，时间复杂度 \(\mathcal O((n+q) \log n)\)。评测记录。

贪心题，对于每个点 \(u\)，优先取贡献大的儿子消耗，然后若还有剩余，则不断地重复儿子——父亲。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

题目即是求 \(dfn_u \le dfn_x \le dfn_u+siz_u-1,dep_x \le dep_u+k\) 的 \(x\) 里 \(a_x\) 的最小值，裸的二维数点。既然强制在线那就主席树直接做。注意要把 \(dep\) 放在外层因为 \(\min\) 不可差分。评测记录。

分类讨论。链上有偶数个点肯定无解，奇数个点时，容易发现就是在链中点处，分出去的其他链的和。

  • 如果 \(dep_u = dep_v\)，那么它们中点的父亲一直延伸到根节点。此时不满足条件的点都在 LCA 的 \(u,v\) 对应的儿子的子树里。

  • 否则，答案是链的中点的子树大小减去较深的那个点的对应儿子的子树大小。

我们需要求树上 \(k\) 级祖先和 LCA。时间复杂度 \(\mathcal O((n+q) \log n)\)。如果使用 st 表求 LCA 并配合长链剖分求树上 \(k\) 级祖先可以做到 \(\mathcal O(n \log n + q)\)。评测记录。

Count on a tree 双倍经验。评测记录。

dp。和在序列上的版本是有些类似的，但是要考虑的更多。设 \(f_{u,i,0/1}\) 表示 \(u\) 的子树内二进制第 \(i\) 位是 \(0/1\) 的方案数，则对于每个点 \(u\) 和其儿子 \(v\)，会产生 \(\sum\limits_i2^i(f_{u,i,0}f_{v,i,1} + f_{u,i,1}f_{v,i,0})\) 的贡献。 dp 转移时，根据 \(a_u\) 二进制位的 \(0/1\) 的到方程：\(f_{u,i,j} = \sum\limits_{v}f_{v,i,k \oplus j}\)，其中 \(k\) 是 \(a_u\) 二进制下的第 \(i\) 位。记得考虑单点的贡献，即最后答案加上 \(\sum\limits_{i=1}^n a_i\)。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

本来想的离线二维数点，但是发现差分一下就做完了。。。时间复杂度 \(\mathcal O(n+m)\)。评测记录。

把每个点拆成两个点，一个代表 \(0\)，一个代表 \(1\)，并把 \(0 \to 1\) 连边。然后我们对于所有边，如果边权是 \(1\) 就在 \(1\) 图，否则在 \(0\) 图。只包含 \(0\) 或 \(1\) 的路径统计是简单的，考虑如何计算同时包含 \(0,1\)。把每个点当转折点统计贡献，答案是 \(0\) 的入边数乘上 \(1\) 的出边数。你发现这个数量就是连通块大小，并查集统计即可。时间复杂度 \(\mathcal O(n \log n)\)，写了按秩合并就是 \(\mathcal O(n\alpha(n))\)。评测记录。

考虑人类智慧：枚举每个位置当最大值，找到左边右边第一个大于它的位置，枚举短区间在长区间寻找答案。提交一发，你发现 AC 了。考虑证明。每一次大区间裂成小区间，较短的那个长度至少减半，所以时间复杂度是 \(\mathcal O(n \log n)\)。评测记录。

由于是二进制，考虑从大到小贪心加点。我们本质要求的是极小连通子树的大小，若这个大小小于等于 \(n-k\)，我们就加入这个点。现在要做的是动态加点，求极小连通子树。这是一个经典问题，维护 dfn 序使用 set 做即可。时间复杂度 \(\mathcal O(n \log n)\)。由于倍增常数巨大，跑得飞慢 qwq。评测记录。

AC 后看题解发现我数据结构学傻了……

容易想到的是计算所有 \(y-x\) 并去掉 \(|y-x| \le 1\) 的贡献。那你发现树状数组就可以解决，然而值域很大，我们树状数组开 map，时间复杂度 \(\mathcal O(n \log^2 V)\)。

但是很遗憾，这个复杂度不够优秀，TLE 了。先离散化数组，注意把 \(a_i+1,a_i-1\) 一起离散化避免错误。这样的时间复杂度是 \(\mathcal O(n \log V)\)，可以通过。注意开 __int128。评测记录。

【】翻译是错的，这题要输出所有可能的最优方案。

妙妙题。我们记下每个叶子节点的 dfn 序，问题转化成序列上的区间问题。我们差分一下，显然原数组全 \(0\)，差分数组也全 \(0\)，而差分数组的和不会因为区间加而改变，所以只有 \(n+1\) 位置可以非 \(0\)。我们把一个区间视作一条 \((l,r+1)\) 的无向边，跑最小生成树即可。这个题很答辩的是要输出方案，而方案是所有在最小生成树里的边的并。需要在 kruskal 时特判。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

题目这个形式就很图论，考虑合法的条件。\(a_{i,j} = \max(a_{i,j},a_{j,k},a_{k,i})\)，即每一条边都是任意一个环上的非严格最大值。我们求 MST，如果加边时，两者已经在同一并查集，那么必然无解。注意考虑相同边权，不然会寄寄。时间复杂度 \(\mathcal O(n^2 \log n^2)\)。评测记录。

二进制划分。题目给了 \(19\) 次询问，正好是 \(2 \log_2 n - 1\)。题目中的询问本质上告诉我们的是，一个集合里 \(y\) 出现次数的奇偶性。我们通过二进制划分，每次询问二进制第 \(i\) 位是 \(1\) 的下标，得到两个出现位置 \(p,q\) 的异或值 \(p \oplus q\)。然后选择一个出现次数是奇数的划分，二分得到一个位置。由于某一位是 \(1\) 的下标位置不会超过 \(\dfrac{n}{2}\)，所以二分只需要 \(9\) 次询问，刚好用完 \(19\) 次询问。评测记录。

VP 的时候遇到的题。设 \(A,B,C\) 的公差分别为 \(d_a,d_b,d_c\)，则 \(d_c = \operatorname{lcm}(d_a,d_b)\)。我们枚举 \(d_a\)，先检验是否有上式成立，然后对于非无穷解的情况，贡献为 \((\dfrac{d_c}{d_a})^2\)。当左端点或右端点比 \(B\) 更向外时，有无穷解。当 \(C\) 的左右端点 \(B\) 里根本没有时，无解。有一些特殊细节，判掉即可。时间复杂度 \(\mathcal O(\sqrt{d_b} \log d_b)\)。评测记录。

先找到基环树的环，然后枚举环上的每一条边。我们发现暴力重算直径是 \(\mathcal O \left(n^2\right)\)，不能通过。首先环外的每一棵子树的直径是与断开边无关的，我们预处理出来环上每一个点的子树直径，记作 \(a_i\)。断环为链，断开每一条边后，直径有三种可能：是左边的两个点，是右边的两个点和一个在左边一个在右边。我们记录下链长的前缀和 \(d_i\)，以第一种情况为例，环上一条路径的长度是 \(a_i + d_i + a_j - d_j \left(i < j\right)\)。只需要在枚举 \(i\) 时记录 \(a_i - d_i\) 的最值即可。另外两种情况计算方法类似。时间复杂度 \(\mathcal O\left(n\right)\)。 评测记录。

好题好题。 /kel

观察到数组内所有元素都是 \(2\) 的正整数次幂，而模数也是，考虑找一些性质。我们发现一个区间 \([l,r]\) 做连续幂运算，得到的结果是 \(2^{b_l2^{\sum_{i=l+1}^r b_i}}\)。模数是 \(2^{2^{20}}\)，也就意味着如果 \(b_l2^{\sum_{i=l+1}^r b_i} \ge 2^{20}\)，贡献一定是 \(0\)。这样一来，我们只需要考虑长度 \(\le 20\) 的区间。

我们枚举一个区间，钦定区间内所有符号填乘方，考虑外面有多少种填符号的方式，方式的数量就是这个区间最后对答案的贡献次数。因为贡献是异或，我们只需要关系这个数量对 \(2\) 取模的结果。考虑外面的空位数量 \(p = n-1-(r-l)-[l \ne 1] - [r \ne n]\)，当 \(l \ne 1,r \ne n\) 时我们要钦定两边填异或。类似的，外面还至少需要填的异或数量是 \(q = k-[l \ne 1] - [r \ne n]\)。那么它对答案的贡献即是：

\[\begin{aligned}ans &= \sum \limits_{i=q}^p\dbinom{p}{i}\\ &= 2^p - \sum \limits_{i=0}^{q-1}\dbinom{p}{i}\\&= \sum \limits_{i=0}^{q-1} \dbinom{p}{i} \pmod 2\\ &= \dbinom{p-1}{q-1} \pmod 2\end{aligned} \]

我们知道组合数 \(\dbinom{n}{m}\) 模 \(2\) 为 \(1\)，当且仅当二进制下 \(m\) 是 \(n\) 的子集。我们只需要枚举每一个区间，计算答案即可。时间复杂度 \(\mathcal O(n \log V)\)，其中 \(V = 2^{20}\)。评测记录。

本质上问的是，只由 \(0\) 边构成的图的连通块个数 \(-1\)。先找到 \(0\) 度数最大的点选择，连接这个点的所有 \(0\) 边。对于剩下的点，暴力枚举点对连边。可以证明最大节点的 \(1\) 度数不会大于 \(k=\dfrac{2m}{n}\)，复杂度是 \(\mathcal O(k^2+nk) = \mathcal O(n+m)\)。评测记录。

抽象而巧妙。忽略边权和的限制，先考虑一条数轴的情况，这是简单的。我们钦定到达位置 \(i\) 的异或和是 \(i-1\)，则 \(i \to i+1\) 的边权值为 \(i\)。因为回头路会抵消，最终返回的 \(x\) 就是最后的位置。放到网格图里，naive 的思路是一半表示行，另一半表示列，但是计算后发现总长度是 \(1.3 \times 10^5\)，寄寄。考虑优化。

  • 优化一：格雷码优化，减少 \(1\) 的数量。将第 \(i\) 个点的权值改为格雷码的第 \(i\) 位，边权改为格雷码相邻项的异或值，总长度降到 \(8 \times 10^4\) 左右。

  • 优化二：奇偶位优化，降低 \(1\) 的权值。我们发现对于前一半，每个 \(1\) 带来的贡献很大，很浪费。因此考虑第 \(0,2,4,6,8\) 和 \(1,3,5,7,9\) 位分开维护信息，最终长度在 \(4.7 \times 10^4\) 左右。

评测记录。

考虑用 kruskal 求出所有可能出现在最小生成树里的边数量，我们一定可以通过某种方式只修改这些边并让最小生成树唯一。因此，答案是这些边的数量减去树边的数量。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

如果 \(n \le 1000\)，这就是很经典的分层图最短路问题。可惜，\(n\) 太大，层间连边过多，如果直接跑，复杂度会达到 \(\mathcal O(kn^2\log kn^2)\)。

我们观察层间连边的边权形式，平方很容易想到斜率优化。我们设 \(f_i\) 表示到点 \(i\) 的最短路，层内跑最短路，层间 dp 转移，使用斜率优化，时间复杂度 \(\mathcal O(km \log m+kn)\)。评测记录。

怎么题解区都是树形 dp 啊 /fn /fn。直接寻宝游戏就好。评测记录。

【模板】线段树分治。双倍经验。评测记录。

考虑加边，合并连通块会使得连边总数减少，因此贪心的取 \(siz\) 最小的两个连通块。此时，计算 \(r = \sum\limits_{i}\min(siz_i,k)\)，\(i\) 是连通块，则 \(\dfrac{r}{2}\) 就是我们可以连的边数，判断是否大于连通块数量 \(-1\) 即可。最多 \(n\) 个连通块，时间复杂度 \(\mathcal O(n \log n)\)。

vp 时遇到的题。考虑列出 \(\mathcal O(n^2)\) 的朴素 dp 式子：\(f_i = \max\{f_j+w_{j+1,i}\}\)。然后开两个树状数组，维护前缀前缀和 \(\max\)、后缀前缀和 \(\max\) 和等于前缀和 \(\max\) 即可，时间复杂度 \(\mathcal O(n \log n)\)。

基本的思路是，设答案为 \(k\)，用这 \(k\) 个放在不同行列，用对角线覆盖 \(n-k\) 的方格，如图。

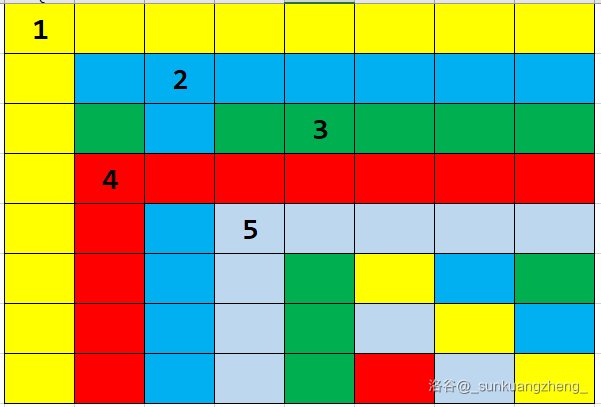
你发现 \(n-k\) 的方格有 \(2(n-k)-1\) 条对角线，所以列出式子：\(k \ge 2(n-k)-1\)，即 \(k \le \lfloor \dfrac{2n+1}{3} \rfloor\)。我们每一行放的位置是下面对应的对角线和行的交点。评测记录。

我们知道 \(x \operatorname{and} y = 0\) 等价于 \(x\) 是 \(y\) 二进制补集的子集。考虑建类似“分层图”的东西，每一个二进制只向和它差一位的数字连边。然后在图上 dfs 数连通块。时间复杂度 \(\mathcal O(n2^n)\)。评测记录。

考虑最简单的无解条件：所有点的度数都大于点权。从这里入手，我们找到一个 \(w_u \ge d_u\) 的点 \(u\)，它的连边的删边顺序一定都不会对答案造成影响，我们希望最后删除这些边，最大化对别的点的贡献。把所有点按 \(d_i - w_i\) 排序扔进 set，每次取出最小值，给其连边的 \(d \gets d-1\)，重复这一过程直到结束。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

找到所有相交区间并相互连边，发现你要干的等价于判断这张图是否是二分图。染色法。时间复杂度 \(\mathcal O(m^2)\)。评测记录。

经典结论是，存在长度大于 \(1\) 的奇数长度回文串，一定要存在长度为 \(3\) 的回文串。现在的问题即为，求满足 \(a_i \ne a_{i+2}\) 的序列 \(a\) 数量。你发现按奇偶性拆成两部分，两部分完全无关，我们分别求解后乘起来。

对于每一部分，考虑 dp 求解。设一段区间两端元素是 \(a_l,a_r\)，\(f_{i,0/1}\) 表示考虑前 \(i\) 个元素，\(a_i = a_r\) 和 \(a_i \ne a_r\) 的方案数量，转移显然。注意根据 \(a_l = a_r\) 是否成立确定边界值。最后，把每一段区间所有数量乘起来即可。时间复杂度 \(\mathcal O(n)\)。评测记录。

区间加不好操作，我们转化成在差分数组上的操作。我们希望，差分数组的字典序尽可能的小，在第一个非 \(0\) 项小于 \(0\) 时，新数组一定比旧答案更优。我们维护一个 map，下标为键，差分数组为值，每次删除 map 最开始所有 \(0\) 项，然后判断第一项是否为负数。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

考虑有解的充要条件：存在两个有边相交的环。此时，我们可以以相交部分的端点为起点终点，找到三条路径。问题转化为如何找到环。

巧妙的思路是先找一棵原图的生成树，对每一条非树边，给它在树上的路径的边边权 \(+1\)。如果存在边权 \(\ge 2\) 的边，那么一定存在两个相交环。这个可以简单树上差分完成。

到这里都是很好写的，但是我们要输出方案，那么首先要找到两个公共端点。最暴力的思路是，类似于求树的直径，两次 dfs 找到两个端点，当然这种做法是可行的。然后，我们需要输出树上路径，最暴力的思路是以端点为根 dfs，不断跳父亲。然后就做完了。注意图不连通，那么对每个连通块跑一遍就行。时间复杂度 \(\mathcal O(n+m\log m)\)。评测记录。

康托展开基础练习题。考虑一个排列的排名式子：\(rk= \sum \limits_{i=1}^na_i(n-i)!\)，\(a_i\) 是除去填过的，比 \(i\) 小的数字个数。将两个排名相加，易得 \(rk = \sum\limits_{i=1}^n(a_i+b_i)(n-i)!\)。当然，这个式子需要取模，但是 \(n!\) 我们不能计算。我们知道，\(n! = n(n-1)!\)，也就是说，对于 \(i \in [1,n-1]\)，如果 \(a_i +b_i \ge n-i+1\)，我们可以向前进位。然后这题就变成了 UVA11525，可以二分树状数组两只 \(\log\) 做，也可以平衡树或者线段树二分一只 \(\log\) 做。评测记录。

矩阵乘法基础练习题。矩阵乘法有结合律和分配律，我们可以用线段树维护区间和。要做的操作有，区间乘矩阵，区间求和，线段树即可。时间复杂度 \(\mathcal O(n \log n)\)，带 \(4\) 倍常数。评测记录。

每个点度数都是偶数是存在欧拉回路的充要条件，那么我们统计度数，两两配对。但是，题目要求入度和出度都是偶数，意味着如果 \(m\) 是奇数，必然存在入度为奇数的点，需要连自环。然后跑欧拉回路，类似 \(a \to b \gets c \to d\) 去定向。评测记录。

我们知道邻接矩阵的 \(k\) 次方表示恰好经过 \(k\) 条边的路径数量，当然在本题里我们只关心可达性。按照边的 \(d\) 值给所有边从小到大排序，每次乘上邻接矩阵的 \(d - d_{lst}\) 次方。然后把可达的点放进队列，跑一遍 bfs 求出最短路即可，最后所有答案取 \(\min\)。时间复杂度 \(\mathcal O(n^3m \log d)\)，并不能过。bitset 优化矩乘即可，时间复杂度 \(\mathcal O(\dfrac{n^3m \log d}{w})\)。评测记录。

我们把排列看作一个一个的环，对每个环上每个元素考虑贡献。为了方便，以下将题意转化为：可以选 \(k\) 个位置，最大最小化可以得到礼物的人的数量。

先考虑最小值，这一部分很简单。我们考虑一个环，如果隔一个选一个，贡献一定是 \(0\)。对于一个环，你可以以 \(0\) 的贡献选 \(\lfloor \dfrac{n}{2} \rfloor\) 个位置。然后考虑填入间隔。如果这是奇环，第一次填贡献是 \(1\)，之后都是 \(2\)；对于偶环，每一个位置都是 \(2\)。我们简单贪心即可，先把贡献 \(0\) 的选完，然后选贡献 \(1\) 的，最后选 \(2\)。

对于最大值，我们希望连续填入。对于一个环，第一次贡献是 \(0\)，最后一次贡献是 \(2\)，除此以外都是 \(1\)。很自然的贪心想法是，按环长从小到大排序去取，但这是错误的。考虑有 \(2\) 个环大小为 \(2,3\)，你可以选 \(k=3\) 个人，此时选大环贡献是 \(3\)，而小环贡献是 \(2\)。仔细思考，你发现一个环的贡献和永远是其大小，我们只需要关心 \(k\) 所在的环能否选到 \(2\)，即第 \(k\) 次选是否能恰好选完一个环。对环的大小做可行性 01 背包，就算用 bitset，复杂度仍是 \(\mathcal O(\dfrac{n^2}{w})\)，无法通过。

本题一个重要性质是，所有物品大小和等于 \(n\)，即使所有环大小不同，也只会存在 \(\sqrt n\) 个本质不同的大小。当然，每个大小会有很多，因此我们进行二进制拆分优化，然后再套可行性 01 背包，时间复杂度 \(\mathcal O(\dfrac{n \sqrt n \log n}{w})\)。评测记录。

贪心。先求出不包含 \(s,t\) 的边构成的各种连通块，然后考虑包含 \(s,t\) 的边，考虑其另一端的连通块 \(v\)。如果只被一个连通，那么必须连；否则，取还能连边多的点连边。注意需要有一个连通块同时连通两边。时间复杂度 \(\mathcal O(n \log n)\)，当然你可以按秩合并优化到几乎线性。评测记录。

考虑 MEX 等于 \(x\) 意味着 \(1 \sim x-1\) 出现在一条链上，用线段树维护值对应的点，现在需要判断若干个点是否在一条链上。我们每一次合并两段链，如何判断能否合出新链？简单的方法是，把四个端点按照 dfs 序排序，计算极小连通子树的大小。如果四个点在一条链上，那么第一个点和最后一个点的距离一定等于这个大小，据此合并即可。每次查询时，可以在线段树上二分，也可以直接二分，使用 st 表求 LCA。用前者的时间复杂度是 \(\mathcal O((n+q) \log n)\)，后者的复杂度是 \(\mathcal O(n \log n + q \log^2 n)\)。评测记录。

先考虑对于一个相同的数字 \(i\)，设出现的 \(c_i\) 个位置是 \(p_1,p_2,\ldots,p_{c_i}\)，它的贡献是什么？容易发现，每一个数字有加的贡献和减的贡献，简单推导可以求出值为 \(\sum \limits_{j=1}^{c_i}(2j-1-c_i)p_j\)。我们计算出所有 \(i\) 的所有系数，现在只需要求 \(\sum\limits_{i=1}^nia_i\)，\(a_i\) 是系数数组。由排序不等式得，将 \(a_i\) 从小到大排序后填在对应位置上可以最大化。由基础组合数学知识，方案数量是每一个相同的 \(a_i\) 数量的阶乘的乘积。现在我们需要快速计算 \(a\) 数组，发现对于每一个 \(c_i\)，其系数形如 \(1-c_i,3-c_i,\ldots,c_i-3,c_i-1\)，差分即可。时间复杂度 \(\mathcal O(n)\)，如果偷懒用 map 的话就会带 \(\log\)。评测记录。

发现一个基本的性质：若第 \(i\) 个位置填 \(x\)，则 \(\operatorname{MEX}(a_1,a_2,\ldots.,a_i) = x-1\) 或 \(x+1\)。

考虑 \(\mathcal O(n^2)\) 的 dp。设 \(f_{i,0/1}\) 表示到第 \(i\) 个数字，\(\operatorname{MEX} = a_i-1/a_i + 1\) 的方案数量，可以暴力转移： \(f_{i,0} = \sum\limits_{j=1}^{i-1}f_{j,0}[a_i=a_j] + f_{j,1}[a_i=a_j+2]\)，另一种转移同理。 但是观察到题目限制 \(1 \le a_i \le n\)，考虑在值域上 dp。设 \(f_{i,x,0/1}\) 表示前 \(i\) 个数字的 \(\operatorname{MEX} = x\)，且 \(a_k=x-1/x+1\) 的方案数量（\(a_k\) 表示最后一个数字），分类讨论进行转移。

  • 前 \(i\) 个数字的 \(\operatorname{MEX} = x+1\)，新状态最后一位仍填 \(x\)。

  1. 前 \(i-1\) 个数字的 \(\operatorname{MEX} = x+1\) 且最后一位是 \(x\)，这一位不填。

  2. 前 \(i-1\) 个数字的 \(\operatorname{MEX} = x+1\) 且最后一位是 \(x\)，这一位填 \(x\)。

  3. 前 \(i-1\) 个数字的 \(\operatorname{MEX} = x\) 且最后一位是 \(x-1\)，这一位填 \(x\)。

对应的转移是 \(f_{i,x+1,0} = 2f_{i-1,x+1,0} + f_{i-1,x,0}\)。

剩余情况转移基本类似。最后省掉第一维，时间复杂度 \(\mathcal O(n)\)。评测记录。

大概计算一下，发现询问次数是 \(5 \log_2 n\) 左右，容易想到二分、二进制分组等算法。但是很遗憾，我们很难利用这些算法求出最终的 \(x\)。考虑每一次将一个集合分为 \(3\) 段，第一次询问第一段，如果是 \(\texttt{No}\) 就再次询问，分类讨论：

  • 得到了 \(\texttt{No}\)。

两次询问都是 \(\texttt{No}\) 证明交互库没有说谎，直接删除第一段。

  • 得到了 \(\texttt{Yes}\)

这种情况相对复杂，我们询问第二段。

  1. 得到了 \(\texttt{Yes}\)。

如果第一段确实是 \(\texttt{Yes}\)，那么 \(x\) 一定不在第三段；否则，这次询问一定是真，\(x\) 也不在第三段，故删除第三段。

  1. 得到了 \(\texttt{No}\)

类似的，直接删除第二段。

每一次都会减少 \(\dfrac{1}{3}\) 的大小，最终只剩 \(2\) 个元素时暴力尝试。询问次数不会超过 \(80\)。评测记录。

巧妙的思路是把 \((a_i,b_i)\) 看作一条线段，\(|a_i - b_i|\) 是线段长度。你可以交换两个端点。接下来我们分类讨论两条线段的位置关系。

  • \(a\) 和 \(b\) 不交

此时交换肯定不优，答案一定变大。

  • \(a\) 和 \(b\) 相交或包含

此时两个线段都会减少两个线段的交，答案减少 \(2|a \cap b|\)。

问题转化成找到两个线段，使得 \(|a \cap b|\) 最大。给所有 \([l,r]\) 排序后维护小于等于当前 \(l\) 的最大 \(r\) 可以很简单的做。

但是你 WA 了，因为你只能交换 \(b\)。简单分析，只有 \((a_i-b_i)(a_j-b_j) < 0\) 你才能交换，维护两个即可。时间复杂度 \(\mathcal O(n \log n)\)。评测记录。

挺好的题啊，为什么做的人这么少 /kel

首先有两个很显然的性质：

  • 性质 \(1\)：若重排 \([l_1,r_1]\) 可以使原序列回文，则对于任意 \(l_2 \in [1,l_1],r_2 \in [r_1,n]\)，重排 \([l_2,r_2]\) 都可以使原序列回文。

  • 性质 \(2\)：设去除掉首尾极长回文段后的区间是 \([l,r](r = n-l+1)\)（形式化的，\(\forall i \in [1,l),a_i = a_{n-i+1}\) 且 \(a_l \ne a_r\)），则任意合法区间都至少包含 \(l,r\) 中的一个。

性质 \(2\) 决定了我们选择的区间一定包含 \([l,r]\) 的前缀或后缀，而性质 \(1\) 决定了确定这个前后缀的长度可以二分。假设我们可以 \(\mathcal O(n)\) 判定一个区间是否合法，考虑怎么计算答案。

首先去除掉首尾的极长回文段，得到区间 \([l,r]\)。我们二分两次，第一次二分出一个 \(p\) 表示 \([l,p]\) 是最短的以 \(l\) 为左端点的合法区间，第二次二分出一个 \(q\) 表示 \([q,r]\) 是最短的以 \(r\) 为右端点的合法区间。显然，一个合法区间 \([x,y]\) 需要满足以下条件中的至少一个：

  • \(x \le l,y \ge p\)。满足该条条件的区间数量是 \(l(n-p+1)\)。

  • \(x \le q,y \ge r\)。满足该条条件的区间数量是 \(q(n-r+1)\)。

当然，我们需要减去算重复的，即同时满足两个条件的区间，也即 \(x \le l,y \ge r\) 的区间，共 \(l(n-r+1)\) 个。那么，最终的答案就是 \(l(n-p+1)+q(n-r+1)-l(n-r+1)\)。

要注意一下，有无论如何重排都不合法和无论如何重排都合法的情况，记得特判掉，防止出现意外错误。

接下来需要考虑这样一个问题：给定区间 \([l,r]\)，问重排 \([l,r]\) 内元素可否使原序列回文。

考虑回文的限制很严格，很多位置的值其实是可以根据已经填好的位置直接确定的。关于序列对称的两个位置都不确定的，一定是中间的一段区间。此时，分 \(n\) 的奇偶性讨论：

  • \(n\) 是偶数。所有未填的元素均要出现偶数次。

  • \(n\) 是奇数。需要有恰好一个元素出现奇数次，其余元素出现偶数次。

体现在程序上，首先计算出 \([l,r]\) 里元素的出现次数，然后我们按照 \(1 \sim \lceil\dfrac{n}{2}\rceil\) 的顺序枚举 \(i\)，分情况讨论：

  • 如果 \(a_i\) 和 \(a_{n-i+1}\) 都已经确定，直接判断是否相等。如果不等，说明区间不合法。

  • 如果 \(a_i\) 和 \(a_{n-i+1}\) 恰好有一个不确定，显然不确定的位置只可以填另一个位置的值，让这个值出现次数 \(-1\)。

  • 如果 \(a_i\) 和 \(a_{n-i+1}\) 都不确定，证明已经到了中间段。直接根据上面的判断条件判断即可。

这部分的时间复杂度 \(\mathcal O(n)\)，因此总的时间复杂度是 \(\mathcal O(n \log n)\)。

先考虑 \(n\) 是奇数的情况，这种情况较为简单。

考虑我们把数字除 \(1\) 外两两分组，\((1),(2,3),(4,5),(6,7),\ldots\)，这些数对内数字除以 \(2\) 下取整相等。如果我们一次询问两个区间 \([1,p],[p+1,n]\)，得到了答案分别为 \(a_1,a_2\)。显然如果一组数字出现在两个区间内，它的贡献会在作差中抵消。因此，我们求出 \(q = a_1 - a_2\) 的值，得到的就是两边区间组数的差值。我们把根据组数差算出的理论长度差 \(2q\) 和区间长度差 \(n-2p\) 比较，由于数组 \((1)\) 的长度少一，如果 \(2q < n-2p\)，则证明 \(1\) 在左边，否则 \(1\) 在右边。一共需要 \(2 \log_2 n \le 20\) 次询问，你发现 G3 已经过了！

考虑 \(n\) 是偶数。注意到此时 \(k=n\) 可以找到 \(n\)。我们直接进行一次二分找到 \(n\) 的位置，再进行上述判断即可，需要 \(30\) 次询问，可以通过 G1。

你发现 \(n\) 到底在哪里并不重要，我们唯一需要用到 \(n\) 的位置的地方在二分时 \(2q = n-2p\)，此时 \(1,n\) 一个在左一个在右。那我们可以直接在这时问出 \(n\) 在哪边啊！此时 \(n\) 的那边被舍弃，我们也不用关心其位置了。现在只需要 \(21\) 次询问，可以过 G2。

找 \(n\) 是必要的，很难去掉这一步，考虑在二分上优化。我们知道二分时，当 \([l,r]\) 的长度仅有 \(2\) 时也需要问两次，有些不划算。考虑利用历史询问信息，由二分的过程，我们一定已经问过了 \([1,l-1],[1,r],[l,n],[r+1,n]\)。如果 \(n\) 不在区间 \([l,r]\) 内，考虑另外一个元素是和左边配对还是和右边配对。假设其和左边配对，那么 \([1,l-1]\) 的答案和 \([1,l]\) 的答案相同时，说明 \(1\) 在 \(r\)，否则在 \(l\)。和右边配对同理。如果 \(n\) 在区间 \([l,r]\) 内，直接问出 \(n\) 的位置就好。只需要 \(2 \log_2 n \le 20\) 次询问。评测记录。

代码其实挺好写的，也挺好调的，我就 WA 了 25 发。

最简单的思路是 \(2^n\) 次询问，当然应该不超过 \(1\) 分钟就能想到先问全 \(\texttt{T/F}\)，枚举每个位置，通过正确数量的差值计算答案。可惜，询问次数是 \(n+1\)，不能通过。

观察询问次数，发现 \(675\) 大概是 \(1000\) 的 \(\dfrac{2}{3}\)，出题人想让我们用两次询问确定三个位置。考虑 \(i,j,k\) 这三个位置，我们用第一次询问问出 \(\texttt{T}\) 的数量 \(a\)。如果 \(a = 0/3\)，我们可以立即判断这三个位置的值。第二次询问，我们询问位置 \(i,j\)，和串 \(\texttt{TFTFTFTF} \ldots\) 的正确数量比较，记差为 \(d\)。如果 \(|d| = 1\)，那么这两个位置肯定相等，可以直接根据 \(a\) 的值确定。否则，可以确定这两个位置的值，再根据 \(a\) 确定第三个位置。记得特判长度 \(\le 2\) 的区间。评测记录。

看到题目第一个想到的就是二进制分组，即对于每个 \(j(0 \le j \le 9)\)，询问二进制下第 \(j\) 位为 \(0\) 和 \(1\) 的下标集合，回答询问时，给答案或上第 \(j\) 位与 \(i\) 这一位值相反的集合。由于不存在两个不同的数字二进制编码相同，所以上面的方法可以遍历到每一个非 \(i\) 元素。但是，它需要 \(20\) 次询问。

观察询问过程，你发现我们的询问方式不太明智，询问过程中大量的信息被重复问到。想要在 \(13\) 次询问内完成交互，我们需要设计一种新的编码方式。

二进制分组时，我们要对每一位是 \(0\) 和 \(1\) 分别问一次，因为可能会存在两个二进制编码，一个是另一个的子集。考虑这样一种编码：不存在两个不等数字，其编码一个是另一个的子集。有这样的编码，我们可以对于每一位只问一次吗？答案是肯定的。

考虑如果编码里不会出现 \(i\) 是 \(j\) 的子集，意味着一定存在两位 \(p,q\)，使得 \(i\) 在第 \(p\) 位上是 \(0\)，第 \(q\) 位上是 \(1\)，而 \(j\) 在这两位上的值正好相反。也就是说，对于所有不等于 \(i\) 的数字 \(j\)，都至少存在一位 \(k\) 满足第 \(k\) 位上 \(j\) 是 \(1\) 而 \(i\) 是 \(0\)。我们可以只询问每一位上是 \(1\) 的下标集合。

如何构造这样的编码？根据询问次数，推断出编码长度应该是 \(13\) 位。我们需要使编码互相不为子集，简单的办法是所有编码 \(1\) 的数量相等。当然，我们需要编码至少能表示 \(10^3\) 个数字，所以我们希望表示的数字尽可能多。显然 \(\dbinom{13}{6} = \dbinom{13}{7}\) 是大于其他 \(n = 13\) 的组合数的，那么我们选择 \(6\) 个 \(1\) 的 \(13\) 位编码即可。计算得知，这样的编码大于 \(1700\) 个，满足要求。评测记录。

首先考虑，如果原矩阵是类型 \(1\)，答案是 \(\texttt{.}\) 的个数；如果是类型 \(2\)，答案是 \(\texttt{.}\) 的数量减去 \(\texttt{V}\) 到边缘的最短路。如果是类型 \(3\)，答案是 \(\texttt{.}\) 的数量减去 \(\texttt{V}\) 到边缘两个不同点的路径的并的最短路。

前两种类型好求，考虑怎么算最后一种。类似于 P6833 的 trick，枚举两条路径的公共部分端点，答案是从这个端点到 \(\texttt{V}\) 的最短路，加上到边缘两个点的最短路和次短路。

但是暴力枚举 bfs 求最短路和次短路的时间复杂度是 \(\mathcal O((n+m)nm)\)，无法通过。我们多源 bfs 同时维护即可，维护每个点的最短路前驱，更新次短路时，只需要这个点不等于前驱即可。时间复杂度 \(\mathcal O(nm)\)。代码非常恶心，不建议写。评测记录。

考虑贪心策略：当对方打出牌 \((a,b)\) 时，你想选择攻击力严格大于 \(b\) 且防御值最大的牌，以减少对方出牌的机会。那么，我们把对应的牌连边，得到一个内向基环森林。显然如果走到环上会平局，否则判断末端是谁即可。时间复杂度 \(\mathcal O(n\log n)\)，瓶颈在建图。评测记录。

首先应该能想到 dp：设 \(f_{i,j}\) 表示考虑前 \(i\) 个，前面有 \(j\) 个红 \(1\) 的最大收益，转移显然，时间复杂度 \(\mathcal O(n^2)\)，能过 \(51\) 个测试点。你发现它很难优化，果断抛弃 dp！

我们看到要么涂红色，要么涂蓝色，想到最小割模型。不考虑数据范围，考虑怎么建模。我们的要求是，如果前面的 \(1\) 和后面的 \(0\) 同时涂红色，应该存在一条 \(s \to 1 \to 0 \to t\) 的路径。那么不难想到这么连边：对于 \(s_i = 0\)，连接 \((s,i,b_i),(i,t,r_i)\)；对于 \(s_i = 1\)，连接 \((s,i,r_i),(i,t,b_i)\)；对于前面的 \(1\) 和后面的 \(0\)，连一条边权为 \(1\) 的边。边数是 \(\mathcal O(n^2)\) 级别的，那么总复杂度是优秀的 \(\mathcal O(n^4)\)，实测 TLE on test 2，甚至不如暴力 dp。

观察到这个图的形式很特殊，考虑贪心求最大流。我们首先让每一条 \(s \to i \to t\) 的路径满流，容易证明这样流不劣。然后，考虑 \(1 \to 0\) 的边，如果对于 \(s_i = 1,r_i \le b_i\)，那么它可以流出的流量全部由 \((i,t)\) 流至汇点，无法外流；如果对于 \(s_i = 0,r_i \le b_i\)，那么它可以汇入的流量全部由 \((s,i)\) 从源点流入，无法接受其他位置的流量。那么，我们得到结论，如果 \(r_i \le b_i\)，可以直接忽略。当然你也可以感性理解：显然多一个位置染红不会减少逆序对数量，而涂红色的收益不大于涂蓝色，那当然直接涂蓝色，不用考虑别的了。

考虑对于剩下的点。如果 \(s_i = 1\)，那么它能为后面的 \(0\) 提供 \(r_i -b_i\) 的多余流量；否则，它可以接受 \(r_i-b_i\) 的流量。我们对于 \(s_i=0\) 的位置考虑，如果前面 \(1\) 的个数大于等于 \(r_i-b_i\)，选择哪些位置流入更优？答案是优先选前 \(r_i-b_i\) 大的。考虑每个位置只能贡献给这个点一次，那么我们希望平均消耗，给后面的 \(0\) 提供尽可能多的位置。为什么 \(1\) 的个数大于等于 \(r_i-b_i\) 就一定要在这个位置流满？考虑把流量让给后面不会使总流量增加，反而可能造成浪费，因此这样正确性就显然了。

总结一下我们要做的事情：

  • 插入 \(r_i-b_i\)。

  • 将前 \(r_i-b_i\) 大的数字 \(-1\)。

  • 查询当前元素个数是否有 \(r_i-b_i\) 个。

  • 删除所有 \(0\)。

我们用 FHQ Treap 维护：操作 \(1,3\) 直接做，操作 \(4\) 可以直接 split，如何处理操作 \(2\)？给每个点维护 \(tag\)，每次操作打 \(tag\)。首先分裂出前 \(k\) 大放到右边，如果左边最大值严格小于右边最小值，那么 \(-1\) 后直接合并；否则需要交叉合并子树。最终时间复杂度 \(\mathcal O(n \log n)\)。代码其实很好写，大部分比较板，没有太多细节。评测记录。

进行一些基本的观察。

性质 \(1\)：若有解，一定有 \(a_1=a_{2n}\)。

证明：每次操作一定会同时取反 \(a_1,a_{2n}\)，因此最开始它们如果不等，一定不能通过若干次操作使它们相等。

性质 \(2\)：若有解，\(a\) 中一定有偶数个 \(1\)。

证明：合法括号序列只能完全包含或者完全不交，而每一个合法括号序列长度都是偶数，所以每次改变的位置数量都是偶数。

现在考虑如何通过这些性质构造。

如果 \(a_1 = 1\) 且 \(\forall i \bmod 2 = 0,a_i = a_{i+1}\)，我们可以通过一次操作把所有数字都变成 \(0\)。具体方法是，对于 \(s_i=s_{i+1}=0\)，我们希望它被覆盖偶数次，而开始时 \(s_1 = \texttt{(}\)，因此填 \(\texttt{()}\)。否则，我们填 \(\texttt{)(}\)，前面的括号和上一个左括号匹配，后一个括号开启新一段。当 \(a = \texttt{1110011001}\) 时，我们构造 \(\texttt{()(())(())}\)。

如何变成上面的形式？忽略 \(a_1\) 的限制，考虑对于每一个 \(i \bmod 2 = 0\)，讨论 \(a_i,a_{i+1}\)。如果 \(a_i = a_{i+1}\)，填 \(\texttt{()}\)，同时取反。否则，填 \(\texttt{((}\) 或者 \(\texttt{))}\)，恰好一位取反。因为有偶数个 \(1\)，因此括号匹配。

如何解决 $a_1 =1 $ 的限制？这是简单的，如果不满足，你只需要 \(\texttt{()()}\) 即可。评测记录。

有意思的题。

先考虑怎么找最大值。显然问 \(n^2-n+1\) 次很浪费。注意到恰有 \(n^2\) 个元素，一次问 \(n\) 个，不难想到分成 \(n\) 组，每次问出一个组里最大的元素，再问一次这些最大的元素中的最大值，询问次数 \(n+1\)。

按照这个思路，再找次大值时仍然分 \(n\) 组，若组内元素不够就从其他组非组内最大值的元素中选一个补上。每一轮询问次数都是 \(n+1\)，总询问次数 \((n^2-n+1)(n+1) = n^3+1\)，在 \(n=0\) 时询问次数符合要求！

考虑这样做还是很浪费询问次数。比如 \(n=3\)，最大值在 \(5\)，两次你会重复询问 \([1,3],[7,9]\)。你发现只有上一次最大值出现的组的组内最大值会改变，我们只需要重问这一个组，这样第一次需要 \(n+1\) 次询问，以后每次需要 \(2\) 次询问，总数量 \(n+1+2(n^2-n)=2n^2-n+1\)，仍然只有 \(n=0\) 时可以通过。

考虑最后剩 \(2n-1\) 个元素的情况。我们有 \(n\) 个组内最大值。显然，一个组内最大值至少会大于 \(n-1\) 个元素，因此这 \(n\) 个数字都不是最小的。我们进行一次询问，问出这 \(n\) 个数字中的最大值，删掉最大值，拿一个后 \(n-1\) 小的数字补上，继续询问。注意你在到 \(2n-1\) 个人的局面时还需要额外问一次组内最大值，总共需要的询问次数 \(n+1+2(n^2-2n)+1+n=2n^2-2n+2\)，正好多一次！

你发现只剩 \(n\) 个人时，那个剩余的唯一组内最大值一定是最大元素，这次询问就省下来了，于是你就 AC 啦！评测记录。

首先你发现如果一个点有 \(\ge 2\) 个儿子，你可以给所有儿子染同色。进一步的，如果不存在只有一个儿子的点，只需要 \(\le 2\) 种颜色。那么考虑只有一个儿子的点怎么办。如果所有只有一个儿子的点深度奇偶性相同，或者都在不同的子树里，那么 \(2\) 种颜色可以解决；否则，按照深度 \(\bmod 3 + 1\) 染色 \(1,2,3\)，只有一个儿子时，根据有哪些颜色就可以找到往上的路。记得判深度为 \(2\) 时只需要一种颜色。评测记录。

一个人存活的时间实际上是 \(h_i \lceil \dfrac{a_i}{x} \rceil\)，取值只有根号种。我们考虑把人按照 \(a_i\) 放在值域上处理，枚举 \(x\)。考虑对于每一个除以 \(x\) 都相等的大块里，你只关心 \(h_i\) 的最大和次大。那么 st 表维护值域上的 \(h_i\) 最大次大，枚举 \(x\) 并暴力枚举块。由调和级数，复杂度 \(\mathcal O(V \log V)\)。略微卡常，记得 st 表 \(2^j\) 一维放外边。评测记录。

最短路，改一改 dij，边权设置为大于当前时间的最早通行时间，直接跑即可。复杂度 \(\mathcal O(m \log m + m \log t)\)。评测记录。

考虑枚举左边的最大值。枚举 \(a_i\) 作为左边的最大值，设 \(l,r\) 是其作为最大值的极长区间的左右端点，则我们找到 \((r,n]\) 内第一个小于 \(a_i\) 的 \(a_x\)，显然左端点 \(L \in [l,r]\)，右端点 \(R \in (r,x)\) 的所有区间 \([L,R]\) 都合法。把 \((L,R)\) 看作平面上的点，题目等价于矩形 \(+1\)，单点查值，差分一下离线二维数点。时间复杂度 \(\mathcal O((n+q) \log n)\)。评测记录。

考虑建一张二分图，左边是行右边是列，一个格子 \((i,j)\) 填数字 \(c\) 则给 \(i\) 行 \(j\) 列对应的点连边，边权 \(c\)。题目转化为找一个长度恰好为 \(4\) 的环且边权互不相同。图中已经有 \(2n\) 条边，易证一定存在长度为 \(2k(k \ge 2)\) 的环。我们每次从中点断环，由于环上原本边权互不相同，不论新边权值为何都有一个环仍满足边权互不相同，继续递归即可。最多操作 \(\log_2 10^3 \le 10\) 次，满足题目要求。注意环长模 \(4\) 的余数不同时环的中点位置不同。评测记录。

设 \(f_{i,j}\) 表示到第 \(i\) 天删除了 \(j\) 条线段的最大空余点数，则有 \(f_{i,j} = \max \limits_{k=1}^{i-1}f_{k,j-x}+1\)，其中 \(x\) 是满足 \(l \in (k,i],r \in [i,n]\) 的区间 \([l,r]\) 数量，因为 \(l \le k\) 的在位置 \(k\) 被消除。直接转移是 \(\mathcal O(n^2k)\) 的，考虑线段树优化。你发现 \(k\) 很小，每层分别维护一个线段树，复杂度 \(\mathcal O(nk^2\log n)\)，卡一卡就过了。评测记录。

好题！

posted @ 2024-01-21 22:17  sunkuangzheng  阅读(50)  评论(0)  编辑  收藏  举报