力扣1235——规划兼职工作

1235. 规划兼职工作

难度困难

你打算利用空闲时间来做兼职工作赚些零花钱。

这里有 n 份兼职工作，每份工作预计从 startTime[i] 开始到 endTime[i] 结束，报酬为 profit[i]。

给你一份兼职工作表，包含开始时间 startTime，结束时间 endTime 和预计报酬 profit 三个数组，请你计算并返回可以获得的最大报酬。

注意，时间上出现重叠的 2 份工作不能同时进行。

如果你选择的工作在时间 X 结束，那么你可以立刻进行在时间 X 开始的下一份工作。

 

示例 1：

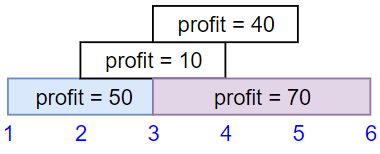
输入：startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出：120
解释：
我们选出第 1 份和第 4 份工作， 
时间范围是 [1-3]+[3-6]，共获得报酬 120 = 50 + 70。

示例 2：

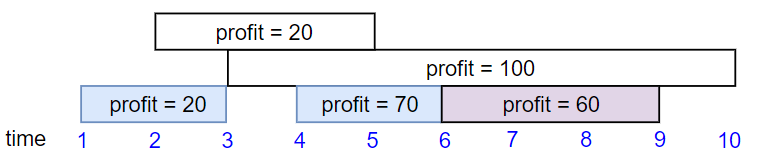
输入：startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出：150
解释：
我们选择第 1，4，5 份工作。 
共获得报酬 150 = 20 + 70 + 60。

示例 3：

输入：startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出：6

 

提示：

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
• 1 <= startTime[i] < endTime[i] <= 10^9
• 1 <= profit[i] <= 10^4

题解

这道题的第一想法就是动态规划，首先将startTime endTime profit放到一个结构体中，按照endTime从小到大进行排序
然后创建一个dp数组，直接使用dp[i] = max(dp[i],dp[starTime]+profit)，但是发现给定的startTime的值最大可以到1e9,
这显示是不能直接使用数组来做的
那么接下来就考虑空间压缩
创建一个pair<int,int>dp[50000+10]数组，first表示endTime结束时间，second表示到该结束时间的总收益
当我们对上面创建的结构体进行排好序之后，就直接遍历结构体数组的每一个元素
当遍历到元素i的时候，使用二分查找dp中找出最大的first小于等于当前开始时间，找出这个dp的index
然后当前收益的最大值就是maxn[index]+profit，而maxn[]数组中存储的就是到dp[index].first为结束时间的最大收益

代码

点击查看代码

class Solution {
public:
    struct Node{
            int startTime,endTime,profit;
            bool operator<(const Node &a)const{
                return endTime < a.endTime;
            }
        }node[50000+10];
    pair<int,int> dp[50000+10]; //first表示endtime  second表示最大利润
    int maxn[50000+10]={0};//存储的是node[0]到node[i]的最大收益
    //二分查找
    int get(int target,int r){//找到dp中的first距离小于等于target中最大的那个first所对应的index
        int l = 0, mid;
        while(l <= r){
            mid = (l + r) >> 1;
            if(dp[mid].first > target) r = mid - 1;
            else l = mid + 1;
        }
        return l - 1;
    }

    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        
        for(int i = 0;i < startTime.size(); i++){
            node[i].startTime = startTime[i];
            node[i].endTime = endTime[i];
            node[i].profit = profit[i];
        }
        sort(node,node + startTime.size());
        dp[0].first = 0;
        dp[0].second = 0;
        maxn[0]=0;
        int nowMaxn = 0;
        for(int i = 0; i < startTime.size(); i++){
            int start = node[i].startTime;
            int end = node[i].endTime;
            int pro = node[i].profit;
            dp[i].first = node[i].endTime; //这里需要注意这句话要在get()之前因为get中的r=i，因此需要提前对i进行赋值         
            //需要注意index有可能是-1,此时说明start比前面dp中所有的first都要小
            int index = get(start,i);
            if(i!=0 && node[i].endTime == node[i-1].endTime) {
                nowMaxn = max(nowMaxn, dp[i-1].second);
            }
            else nowMaxn = 0;
            if(index == -1) {
                dp[i].second = pro;
            }
            else{
                dp[i].second = max(nowMaxn,maxn[index] + pro);
            }         
            maxn[i] = max(dp[i].second,maxn[max(0,i-1)]);
        }

        return maxn[startTime.size() - 1];

    }
};