力扣778——水位上升的泳池中游泳

778. 水位上升的泳池中游泳

难度困难

在一个 n x n 的整数矩阵 grid 中，每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度。

当开始下雨时，在时间为 t 时，水池中的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台，但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离，也就是默认在方格内部游动是不耗时的。当然，在你游泳的时候你必须待在坐标方格里面。

你从坐标方格的左上平台 (0，0) 出发。返回 你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间 。

 

示例 1:

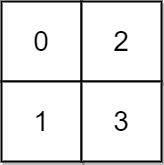
输入: grid = [[0,2],[1,3]]
输出: 3
解释:
时间为0时，你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向，因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时，你才可以游向平台 (1, 1). 因为此时的水位是 3，坐标方格中的平台没有比水位 3 更高的，所以你可以游向坐标方格中的任意位置

示例 2:

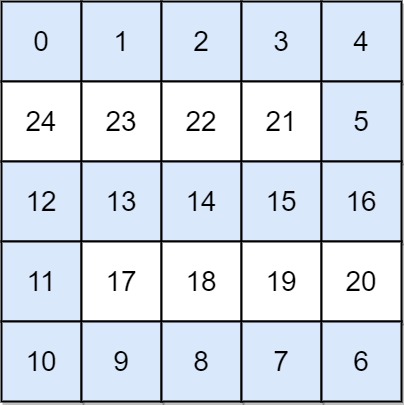
输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
输出: 16
解释: 最终的路线用加粗进行了标记。
我们必须等到时间为 16，此时才能保证平台 (0, 0) 和 (4, 4) 是连通的

 

提示:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] < n2
• grid[i][j] 中每个值 均无重复

题解

虽然在力扣中将这道题标为了困难，但实际上这道题就是一个简单的深搜dfs+剪枝
我们首先创建一个dp的二维数字，因为题目中说给定的grid的元素值都小于nn，因此我们直接让dp中的每个值都初始化为nn，也就是相当于一个无穷大的值
从[0][0]开始进行搜，查看如果从当前位置到下一个位置，会不会使得dp[nexti][nextj]的值变小，也就是是否会更新dp[nexti][nextj]，如果更新，那么
我们继续向(nexti,nextj)进行深搜，如果不变，则不需要向该点进行深搜。
当深搜完毕之后，最后的dp[n-1][n-1]就是我们需要的结果

代码

点击查看代码

class Solution {
public:

    int direct[2][4] = {{1,-1,0,0},{0,0,1,-1}};

    void dfs(int dp[][50],vector<vector<int>>& grid,int i,int j,int n){
        for(int k = 0; k < 4; k++){
            int nowi = i + direct[0][k];
            int nowj = j + direct[1][k];
            if(nowi >= 0 && nowi < n && nowj >= 0 && nowj < n){
                if(dp[nowi][nowj] > max(dp[i][j], grid[nowi][nowj])){
                    dp[nowi][nowj] = max(dp[i][j], grid[nowi][nowj]);
                    dfs(dp,grid,nowi,nowj,n);
                }
            }
        }
    }

    int swimInWater(vector<vector<int>>& grid) {
        int n = grid.size();

        int dp[50][50];
        for(int i = 0; i < n; i++){
            for(int j = 0;j < n; j++){
                dp[i][j] = n * n;
            }
            
        }
        dp[0][0] = grid[0][0];
        dfs(dp,grid,0,0,n);
        return dp[n-1][n-1];

    }
};