算法导论读书笔记（6）

算法导论读书笔记（6）

目录

• 优先级队列
• 练习
  • 6.5-7
  • 6.5-8

优先级队列

堆的一个很常见的应用：作为高效的 优先级队列 （priority queue）。队列也有两种：最大优先级队列和最小优先级队列。

优先级队列 是一种用来维护由一组元素构成的集合 S 的数据结构，这一组元素中的每一个都有一个关键字 key 。一个 最大优先级队列 支持以下操作：

• INSERT(S, x) ：把元素 x 插入集合。
• MAXIMUM(S) ：返回 S 中具有最大关键字的元素。
• EXTRACT-MAX(S) ：去掉并返回 S 中具有最大关键字的元素。
• INCREASE-KEY(S, x, k) ：将元素 x 的关键字值增加到 k ，这里 k 值不能小于 x 的原关键字值。

最大优先级队列的一个应用是在一台分时计算机上进行作业调度。 最小优先级队列 支持的操作包括 INSERT ， MINIMUM ， EXTRACT-MIN ， DECREASE-KEY 。这种队列可被用在基于事件驱动的模拟器中。

下面是最大优先级队列的操作。过程 HEAP-MAXIMUM 用 Θ (1)的时间实现了 MAXIMUM 操作

HEAP-MAXIMUM(A)
1 return A[1]

过程 HEAP-EXTRACT-MAX 实现了 EXTRACT-MAX 操作。

HEAP-EXTRACT-MAX(A)
1 if A.heap-size < 1
2     error "heap underflow"
3 max = A[1]
4 A[1] = A[A.heap-size]
5 A.heap-size = A.heap-size - 1
6 MAX-HEAPIFY(A, 1)
7 reutrn max

HEAP-EXTRACT-MAX 的运行时间为 O (lg n )。

过程 HEAP-INCREASE-KEY 实现了 INCREASE-KEY 操作。

HEAP-INCREASE-KEY(A, i, key)
1 if key < A[i]
2     error "new key is smaller than current key"
3 A[i] = key
4 while i > 1 and A[PARENT(i)] < A[i]
5     exchange A[i] with A[PARENT(i)]
6     i = PARENT(i)

下图是 HEAP-INCREASE-KEY 操作的一个示例。在 n 元堆上， HEAP-INCREASE-KEY 的运行时间为 O (lg n )。

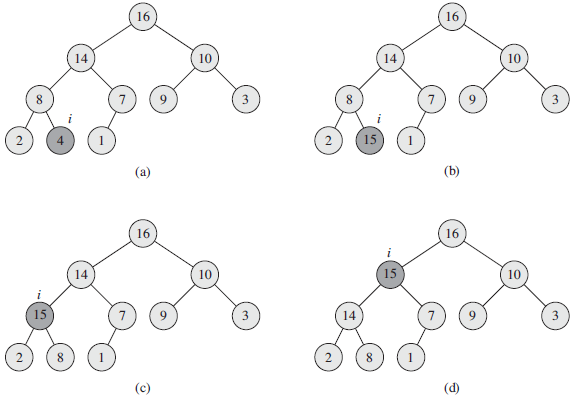
下面的 MAX-HEAP-INSERT 过程实现了 INSERT 操作。

MAX-HEAP-INSERT(A, key)
1 A.heap-size = A.heap-size + 1
2 A[A.heap-size] = -∞
3 HEAP-INCREASE-KEY(A, A.heap-size, key)

该过程的运行时间也是 O (lg n )。

上述过程的参考实现。

练习

6.5-7

给出 HEAP-DELETE 的伪码

HEAP-DELETE(A, i)
1 A[i] = A[A.heap-size]
2 A.heap-size = A.heap-size - 1
3 MAX-HEAPIFY(A, i)

6.5-8

给出一个时间为 O ( n lg n )，用来将 k 个已排序链表合并成一个排序链表的算法。此处 n 为所有链表中元素的总数。（用最小堆做 k 路合并）

问题思路：首先将 k 个已排序链表中的第一个元素取出并放入一个有 k 个元素的数组中，接着使用该数组构造最小堆。然后使用 HEAP-EXTRACT-MIN 过程每次从堆中取出一个元素放入新链表中，然后再从取出元素的原链表中取出下一个元素放入堆中，重复以上步骤直到堆为空。最终的新链表中保存的就是已排序的所有元素。