题意:
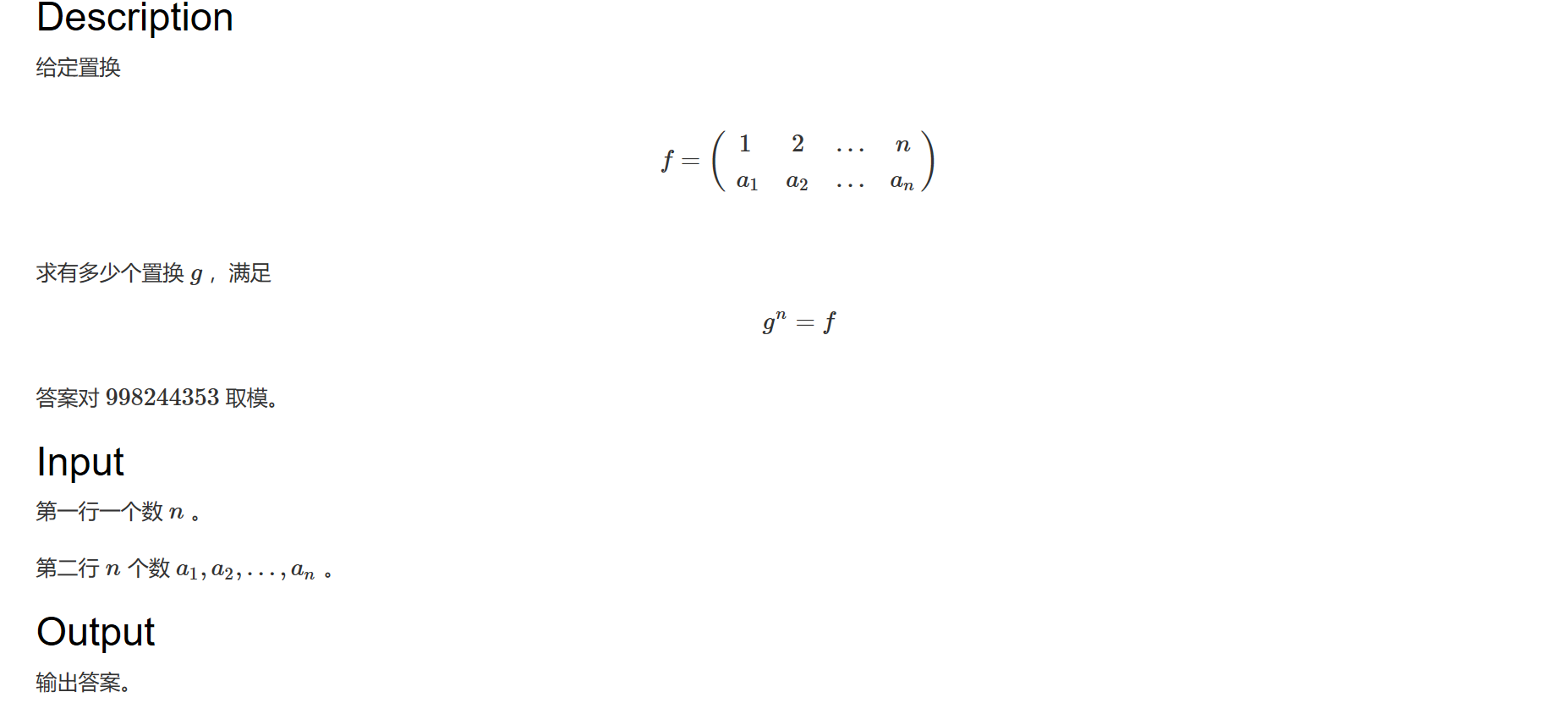
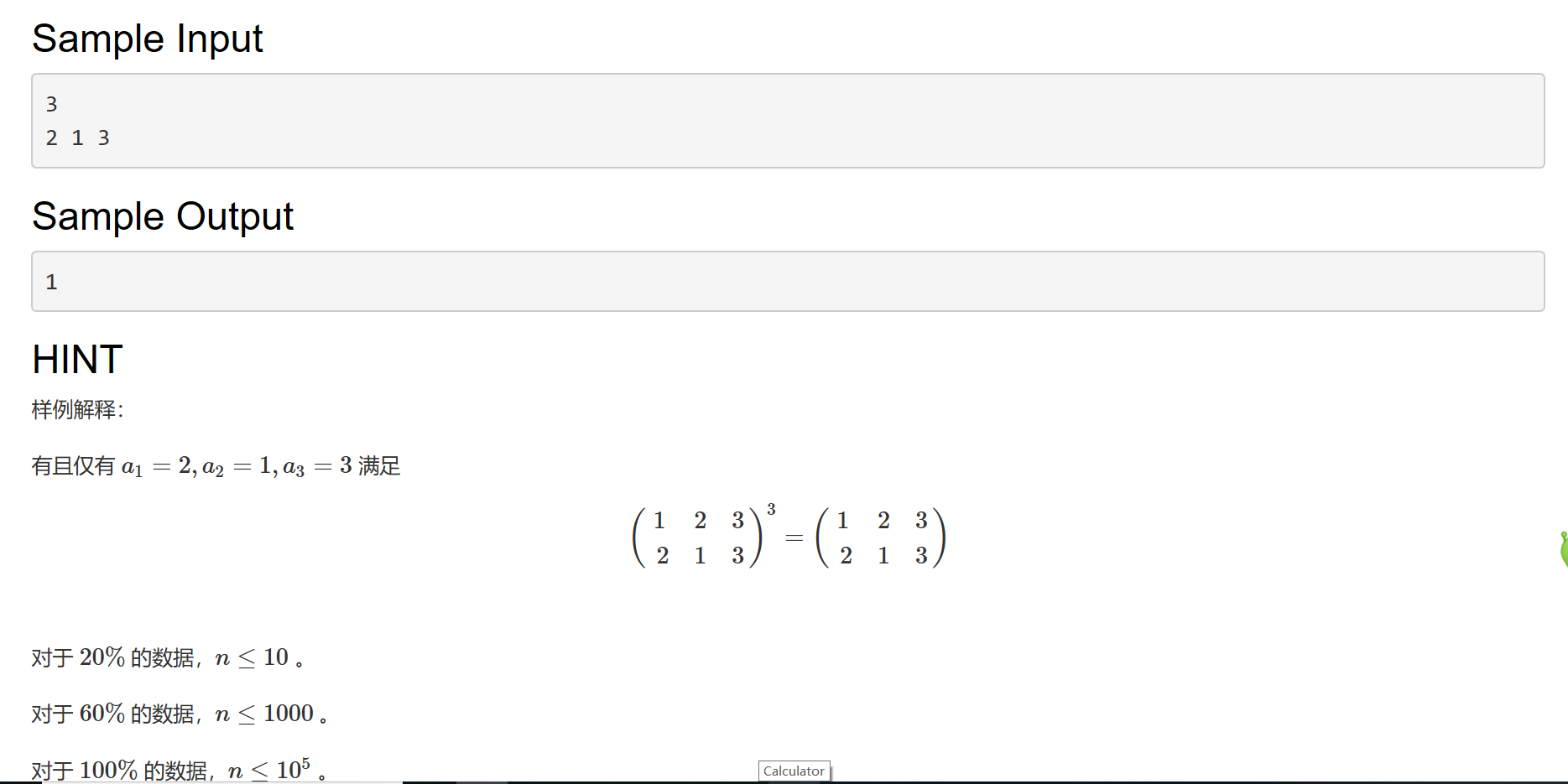
题解: 这道题我思路大方向是正确的,但是生成函数推错导致一直WA,看了标程才改对……
首先一个长为\(m\)的轮换的\(n\)次幂会分裂成\(\gcd(n,m)\)个长为\(\frac{m}{\gcd(n,m)}\)的轮换
所以合并的时候相当于对于一个长度\(l\)若存在一个\(m\)使得\(\frac{m}{\gcd(n,m)}=l\)则\(\gcd(n,m)\)个长度为\(l\)的轮换可以合并
显然不同长度的轮换是互不影响的,那么我们可以分开每种长度计算
就相当于对于一个长度为\(l\)的有标号的轮换,要把它们划分成若干无标号集合,每个集合大小都在给定的集合\(S\)内,并且每个集合有权值(合并的方案数),一种划分方案的权值为所有集合权值之积,求所有划分方案权值总和
那么显然这个东西的EGF就等于\(\exp(\sum_{i\in S} \frac{w_i}{i!})\), \(w_i\)为权值
如何求\(w_i\)? 在这里我出了问题
正确的答案是,假设\(k\)个长度为\(l\)的轮换合并,方案数为\(l^{k-1}(k-1)!\), 也就是\(\frac{l^kk!}{lk}\).
这大概是因为,假设我们定住第一个轮换的第一个元素的位置,那么其余每个轮换自身内部的顺序都可以改变,这样是\(l^{k-1}\)种;这些轮换之间的顺序也可以改变,这样是\((k-1)!\)种。
代码
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<iostream>
#include<vector>
#define llong long long
using namespace std;
inline int read()
{
int x=0; bool f=1; char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=0;
for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0');
if(f) return x;
return -x;
}
const int N = 1<<19;
const int LGN = 19;
const int P = 998244353;
const int G = 3;
llong quickpow(llong x,llong y)
{
llong cur = x,ret = 1ll;
for(int i=0; y; i++)
{
if(y&(1ll<<i)) {y-=(1ll<<i); ret = ret*cur%P;}
cur = cur*cur%P;
}
return ret;
}
llong mulinv(llong x) {return quickpow(x,P-2);}
namespace FFT
{
llong tmp1[N+3],tmp2[N+3],tmp3[N+3],tmp4[N+3],tmp5[N+3],tmp6[N+3],tmp7[N+3],tmp8[N+3],tmp9[N+3],tmp10[N+3];
llong tst1[N+3],tst2[N+3],tst3[N+3];
llong sexp[N+3];
int fftid[N+3];
int getdgr(int n) {int ret = 1; while(ret<=n) ret<<=1; return ret;}
void init_fftid(int dgr)
{
int len = 0; for(int i=1; i<=LGN; i++) {if((1<<i)==dgr) {len = i; break;}}
fftid[0] = 0; for(int i=1; i<dgr; i++) fftid[i] = (fftid[i>>1]>>1)|((i&1)<<(len-1));
}
void ntt(int dgr,int coe,llong poly[],llong ret[])
{
init_fftid(dgr);
if(poly==ret) {for(int i=0; i<dgr; i++) {if(i<fftid[i]) swap(ret[i],ret[fftid[i]]);}}
else {for(int i=0; i<dgr; i++) ret[i] = poly[fftid[i]];}
for(int i=1; i<=(dgr>>1); i<<=1)
{
llong tmp = quickpow(G,(P-1)/(i<<1));
if(coe==-1) {tmp = mulinv(tmp);}
sexp[0] = 1ll; for(int j=1; j<i; j++) sexp[j] = sexp[j-1]*tmp%P;
for(int j=0; j<dgr; j+=(i<<1))
{
for(llong *k=ret+j,*kk=sexp; k<ret+i+j; k++,kk++)
{
llong y = k[i]*(*kk)%P;
k[i] = (*k)-y<0 ? (*k)-y+P : (*k)-y;
(*k) = (*k)+y>=P ? (*k)+y-P : (*k)+y;
}
}
}
if(coe==-1)
{
llong tmp = mulinv(dgr);
for(int i=0; i<dgr; i++) ret[i] = ret[i]*tmp%P;
}
}
void polymul(int dgr,llong poly1[],llong poly2[],llong ret[])
{
ntt((dgr<<1),1,poly1,tmp1); ntt((dgr<<1),1,poly2,tmp2);
for(int i=0; i<(dgr<<1); i++) ret[i] = tmp1[i]*tmp2[i]%P;
ntt((dgr<<1),-1,ret,ret);
}
void polyinv(int dgr,llong poly[],llong ret[])
{
for(int i=0; i<(dgr<<1); i++) ret[i] = tmp3[i] = tmp4[i] = tmp5[i] = 0ll;
ret[0] = mulinv(poly[0]);
for(int i=1; i<=(dgr>>1); i<<=1)
{
for(int j=0; j<(i<<1); j++) tmp3[j] = poly[j];
ntt((i<<2),1,tmp3,tmp4); ntt((i<<2),1,ret,tmp5);
for(int j=0; j<(i<<2); j++) tmp3[j] = tmp4[j]*tmp5[j]%P*tmp5[j]%P;
ntt((i<<2),-1,tmp3,tmp4);
for(int j=0; j<(i<<1); j++) ret[j] = (ret[j]+ret[j]-tmp4[j]+P)%P;
}
}
void polyder(int dgr,llong poly[],llong ret[])
{
for(int i=0; i<dgr-1; i++) ret[i] = poly[i+1]*(i+1)%P;
ret[dgr-1] = 0ll;
}
void polyint(int dgr,llong poly[],llong ret[])
{
for(int i=1; i<dgr; i++) ret[i] = poly[i-1]*mulinv(i)%P;
ret[0] = 0ll;
}
void polyln(int dgr,llong poly[],llong ret[])
{
for(int i=0; i<(dgr<<1); i++) ret[i] = tmp6[i] = tmp7[i] = tmp8[i] = 0ll;
polyder(dgr,poly,tmp6);
polyinv(dgr,poly,tmp7);
polymul(dgr,tmp6,tmp7,tmp8);
polyint(dgr,tmp8,ret);
}
void polyexp(int dgr,llong poly[],llong ret[])
{
for(int i=0; i<(dgr<<1); i++) ret[i] = tmp9[i] = tmp10[i] = 0ll;
ret[0] = 1ll;
for(int i=1; i<=(dgr>>1); i<<=1)
{
polyln((i<<1),ret,tmp9);
for(int j=0; j<(i<<1); j++) tmp9[j] = (-tmp9[j]+poly[j]+P)%P; tmp9[0]++;
polymul((i<<2),ret,tmp9,tmp10);
for(int j=0; j<(i<<1); j++) ret[j] = tmp10[j];
}
}
}
int permu[N+3];
int a[N+3];
int dgr[N+3];
bool vis[N+3];
vector<int> s[N+3];
llong f[N+3],expf[N+3];
llong fact[N+3];
int n;
int gcd(int x,int y) {return y==0?x:gcd(y,x%y);}
int main()
{
fact[0] = 1ll; for(int i=1; i<=N; i++) fact[i] = fact[i-1]*i%P;
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&permu[i]);
for(int i=1; i<=n; i++)
{
if(vis[i]) continue;
int len = 1; vis[i] = true;
for(int j=permu[i]; j!=i; j=permu[j])
{
len++;
vis[j] = true;
}
a[len]++;
}
for(int i=1; i<=n; i++)
{
int g = gcd(i,n),l = i/gcd(i,n);
s[l].push_back(g);
}
llong ans = 1ll;
for(int i=1; i<=n; i++)
{
if(a[i]==0) continue;
int dgr = FFT::getdgr(a[i]);
for(int j=0; j<s[i].size(); j++)
{
if(s[i][j]<dgr)
{
f[s[i][j]] = (f[s[i][j]]+mulinv(s[i][j])*quickpow(i,s[i][j]-1))%P;
}
}
FFT::polyexp(dgr,f,expf);
ans = ans*expf[a[i]]%P*fact[a[i]]%P;
for(int j=0; j<(dgr<<1); j++) f[j] = expf[j] = 0ll;
}
printf("%lld\n",ans);
return 0;
}



