我们的数组
上一篇，我们讲完算法复杂度，接下来我们来见一见我们非常熟悉的朋友--数组。
我们平时使用的数组是数据类型，但是数组不仅仅是数据类型更是一种基础的数据结构。
数组的定义
我们来看看数组定义：分类连续的内存空间来存储相同类型集合的线性表数据结构。
线性表+连续内存+相同类型 着三个特性合并出了数组的必杀技：随机访问。
那么数组是怎么实现下标随机访问的呢？
随机访问
根据头节点和固定类型具体长度，就可以实现随机访问。
search[i]_address = base_address + i*data_type_size
虽然对于访问来讲，下标随机访问的复杂度为O(1)
插入和删除
但是对于插入和删除来说日子就不是那么好过了。
因为数组要保证内存的连续性这个特性，所以插入和删除都是比较低效的，我们具体来看看插入和删除。
插入：我们在任意节点前插入，那么后面的元素必须后移一位来保证连续性。
假设我们有一个数组为 int[n] =[1,2,3,4,5,......,n]
我们在左侧顶头插入呢？后面的全部都移动，所以算个复杂度为O(n)，我们上面一篇提到过的最差情况时间复杂度
与此对应的是末尾插入，完美，啥都不用干，这就不用说了就是 最好情况时间复杂度。
那么如果在中间任意位置出现呢？多种情况，所以就是平均情况时间复杂度
归纳一下：
数组左侧顶头插入元素，最坏情况时间复杂度 O(n)
数组末尾追加插入元素：最好情况时间复杂度 O(1)
数组中间情况插入元素，平均情况时间复杂度 O(n)
插入平均时间复杂度
我们这里来验证一下，数组下标随机访问的平均时间复杂度为什么是O(n)：
对于一个 int[n] = [1，2，3，4，5，......，n]
我从头依次进行插入，那么对应的移动数组次数是
n
(n-1)
(n-2)
...
1
0
对于平均时间复杂度来讲，可以插入的空前后两端2个+中间n-1，即 n+1 种情况
这里的每个插入点发生的情况概率是一样的都是 1 / (n+1）
所以，平均时间复杂度为移动次数*发生的概率
n * [1/(n+1)]
(n-1) * [1/(n+1)]
...
1 * [1/(n+1)]
0 * [1/(n+1)]
简化一下：(0+1+2+3...n) / (n+1) => [(n-1)/2] * n + n / (n+1)
算法复杂度去除系数、常量、低阶，这里的平均情况时间复杂度是O(n)
日常开发中，如果我们遇到有序数组，那我们必须在插入的同时，后移后面的所有位置。
但是如果数组对排序不敏感，那么我们的插入可以在后面追加，这样避免了移动数组，复杂度就是O(1)
删除：如果我们删除数组中的元素，为了保持数组的连续性，依然需要搬运数组元素。
所以删除操作和插入操作的最好、最坏、平均复杂度是对应的。
其实我们也可以加一个删除标记，在空闲的时候进行删除重排序。
访问越界问题
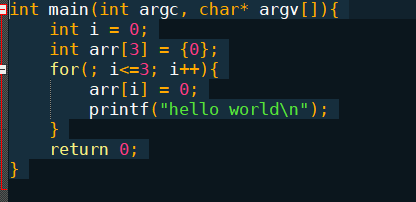
对于以上这段C程序来说，上面这段代码，我们在书写的时候，没有仔细检查，使得<写成了<=，这样就会产生了越界问题。
前提条件：
1、因为不同的CPU架构不同的编译器会有不同的内存分配策略：从高地址向低地址增长，或者从低地址向高地址增长。也就是大小端问题。
2、首先压栈的是 i ，之后是数组arr。所以 i 的内存地址比arr中的元素高，并且 i 和arr中的元素相邻，并且类型相同，也就是子节是对齐的。
所以当 arr [ 3 ] 这个地址越界访问到了 相邻的同类型的 i 这个变量的内存地址。arr[3] =0，其实也就是 i = 0，好吧，又从头开始了，无限循环。
那么为什么我们平时使用的语言即便是越界也会程序异常终止。其实这是编译器做的工作，编译器不同，内存申请方式也不同。
我们平时的编译器已经帮我们做好了代码检查等工作。所以避免了越界的情况。
C# []、Array、ArrayList、List<T>
首先 [] ,就是我们声明简单的数组,因为数组是连续的线性数据结构，所以很多操作微软又给做了封装。
Array ，就是微软对数组进行的封装类。下面又进一步衍生出了动态数组。
ArrayList，就是动态数组，里面封装了数组很多的操作。尤其是动态扩容。泛型之后，又出了泛型列表。
List<T>是动态数组的泛型版本，避免了频繁的装箱拆箱，效率较高，也是我们平时使用最频繁的一种。
其实微软已经开源了.NET Framework 源码，详细可查看此地址。
还有一种方式，可以使用远程调试源码，远程下载源码到本地，进行源码调试：
工具 -》 调试 -》勾选 启用源代码单步调试
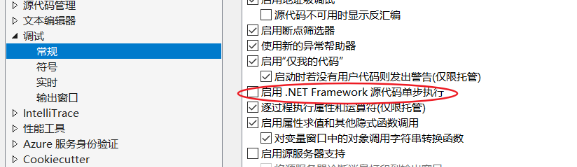
当然速度上肯定会比本地代码慢。
以上就是今天的内容。
