二叉树的遍历递归非递归

重点说一下二叉树后序遍历的非递归实现
创建的二叉树如下：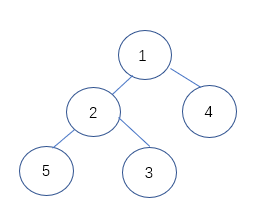

后序遍历为：5 3 2 4 1

先序遍历为：1 2 5 3 4

逆后序遍历为：1 4 2 3 5

从逆后序遍历与先序遍历的关系中我们可以知道逆后序遍历序列为先序遍历交换左右子树的遍历顺序得到的，所以我们得到了逆后序序列之后然后逆序就可以得到后序遍历的序列了，所以需要两个栈，第一个栈用来存储先序遍历交换左右子树的遍历的中介结果，第二个是存储后序遍历的结果（逆序也就是可以理解为先进后出的意思）

下面是模仿元素进栈与出栈的过程：

① 1节点进栈，在循环中弹出1节点压入到第二个栈中，发现左右节点不为空那么将左右节点压入栈1，这个与先序遍历中将左右子树压入到栈顶的顺序是相反的

② 弹出4节点压入到第二个栈中，发现左右孩子都为空那么不进行任何的操作

③ 弹出2节点压入到第二个栈中，发现左右节点不为空那么将左右节点压入到栈1中

④ 弹出3节点压入到第二个栈中，发现左右孩子都为空不进行任何操作

⑤ 弹出5节点压入到第二个栈中，发现左右孩子都为空不进行任何操作

最后栈为空那么退出循环结束
代码：

public class 树的遍历 {
    //前序 递归
    public static void preOrderTraversal(int[] nums, int i) {
        if(i >= nums.length || nums[i] == -1) {
            return;
        }
        System.out.print(nums[i] + " ");
        preOrderTraversal(nums, 2 * i + 1);
        preOrderTraversal(nums, 2 * i + 2);
    }
    //前序 非递归
    public static void preOrderTraversal2(int[] nums, int i) {
        LinkedList<Integer> list = new LinkedList<>();
        //i < nums.length && nums[i] != -1表示nums[i]存在
        while(i < nums.length && nums[i] != -1 || !list.isEmpty()) {
            while(i < nums.length && nums[i] != -1) {
                System.out.print(nums[i] + " ");
                list.push(i);
                i = 2 * i + 1;//nums[i]左节点
            }
            i = list.pop() * 2 + 2;//nums[i]右节点
        }

    }
    //中序 递归
    public static void inOrderTraversal(int[] nums, int i) {
        if(i >= nums.length || nums[i] == -1) {
            return;
        }
        inOrderTraversal(nums, 2 * i + 1);
        System.out.print(nums[i] + " ");
        inOrderTraversal(nums, 2 * i + 2);
    }
    //中序 非递归
    public static void inOrderTraversal2(int[] nums, int i) {
        LinkedList<Integer> list = new LinkedList<>();
        while(i < nums.length && nums[i] != -1 || !list.isEmpty()) {
            while(i < nums.length && nums[i] != -1) {
                list.push(i);
                i = 2 * i + 1;
            }
            int k = list.pop();
            System.out.print(nums[k] + " ");
            i = k * 2 + 2;
        }
    }

    //后序 递归
    public static void postOrderTraversal(int[] nums, int i) {
        if(i >= nums.length || nums[i] == -1) {
            return;
        }
        postOrderTraversal(nums, 2 * i + 1);
        System.out.print(nums[i] + " ");
        postOrderTraversal(nums, 2 * i + 2);

    }
    
    //后续 非递归 双栈
    public static void postOrderTraversal2(int[] nums, int i) {
        LinkedList<Integer> stack1 = new LinkedList<>();
        LinkedList<Integer> stack2 = new LinkedList<>();
        stack1.push(i);
        while (!stack1.isEmpty()) {
            i = stack1.pop();
            stack2.push(i);//把stack1栈顶的元素压进list中
            i = 2 * i + 1;
            if(i < nums.length && nums[i] != -1)
               stack1.push(i);
            ++i;
            if(i < nums.length && nums[i] != -1)
                stack1.push(i);
        }
        for (int k: stack2) {
            System.out.print(nums[k] + " ");
        }

    }

    //层序遍历 队列实现
    public static void levelOrder(int[] nums, int i) {
        LinkedList<Integer> que = new LinkedList<>();
        que.push(i);
        while(!que.isEmpty()) {
            i = que.removeFirst();
            System.out.print(nums[i] + " ");
            i = 2 * i + 1;
            if(i < nums.length && nums[i] != -1)
                que.addLast(i);
            ++i;
            if(i < nums.length && nums[i] != -1)
                que.addLast(i);
        }
    }

    public static void main(String[] args) {
        int[] nums = new int[]{1, 2, 3, -1, 5, 6, -1};
        postOrderTraversal2(nums, 0);
    }
}