校验码
海明校验码
将K位检测位记作Ci(i=1,2,4,8...)分别安插在n+k位代码编号的第1,2,4,8,16...位上。
01101110(n=8)根据2的k次方大于等于n+k+1,可求出配置成海明码需增添检测位k=4,
原码01101110记作B8,B7,B6,B5,B4,B3,B2,B1.
则原码同检测位的位置安排如下:
二进制序号:1 2 3 4 5 6 7 8 9 10 11 12
名称 C1 C2 B8 C4 B7 B6 B5 C8 B4 B3 B2 B1
如果按配偶原则来配置海明码,则
C1应使1,3,5,7,9,11位中的“1”的个数为偶数;
C2应使2,3,6,7,10,11位中的“1”的个数为偶数;
C4应使4,5,6,7,12位中的“1”的个数为偶数;
C8应使8,9,10,11,12位中的“1”的个数为偶数;
故C1应为3位⊕5位⊕7位⊕9位⊕11位,即C1=B8⊕B7⊕B5⊕B4⊕B2
故C2应为3位⊕6位⊕7位⊕10位⊕11位,即C2=B8⊕B6⊕B5⊕B3⊕B2
故C4应为5位⊕6位⊕7位⊕12位,即C4=B7⊕B6⊕B5⊕B1
故C8应为9位⊕10位⊕11位⊕12位,即C8=B4⊕B3⊕B2⊕B1
即,
C1=B8⊕B7⊕B5⊕B4⊕B2=0⊕1⊕0⊕1⊕1=1
C2=B8⊕B6⊕B5⊕B3⊕B2=0⊕1⊕0⊕1⊕1=1
C4=B7⊕B6⊕B5⊕B1=1⊕1⊕0⊕0=0
C8=B4⊕B3⊕B2⊕B1=1⊕1⊕1⊕0=1
故01101110的海明校验码为C1 C2 B8 C4 B7 B6 B5 C8 B4 B3 B2 B1=110011011110
奇偶校验码
奇偶校验码是一种增加二进制传输系统最小距离的简单和广泛采用的方法。是一种通过增加冗余位使得码字中"1"的个数恒为奇数或偶数的编码方法,它是一种检错码。在实际使用时又可分为垂直奇偶校验、水平奇偶校验和水平垂直奇偶校验等几种。
是一种增加二进制传输系统最小距离的简单和广泛采用的方法。例如,单个的奇偶校验将使码的最小距离由一增加到二 。
一个二进制码字,如果它的码元有奇数个1,就称为具有奇性。例如,码字"10110101"有五个1,因此,这个码字具有奇性。同样,偶性码字具有偶数个1。注意奇性检测等效于所有码元的模二加,并能够由所有码元的异或运算来确定。对于一个n位字,奇性由下式给出:奇性=a0⊕a1⊕a2⊕…⊕an
奇偶校验可描述为:给每一个码字加一个校验位,用它来构成奇性或偶性校验。可以看出,附加码元d2,是简单地用来使每个字成为偶性的。因此,若有一个码元是错的,就可以分辨得出,因为奇偶校验将成为奇性。奇偶校验编码通过增加一位校验位来使编码中1个个数为奇数(奇校验)或者为偶数(偶校验),从而使码距变为2。因为其利用的是编码中1的个数的奇偶性作为依据,所以不能发现偶数位错误。
码距
一个编码系统中任意两个合法编码(码字)之间不同的二进数位(bit)数叫这两个码字的码距,而整个编码系统中任意两个码字的的最小距离就是该编码系统的码距。
为了使一个系统能检查和纠正一个差错,码间最小距离必须至少是"3"。最小距离为3时,或能纠正一个错,或能检二个错,但不能同时纠一个错和检二个错。编码信息纠错和检错能力的进一步提高需要进一步增加码字间的最小距离。
码距越大,纠错能力越强,但数据冗余也越大,即编码效率低了。所以,选择码距要取决于特定系统的参数。数字系统的设计者必须考虑信息发生差错的概率和该系统能容许的最小差 错率等因素。
基本分类
垂直奇偶校验
垂直奇偶校验又称为纵向奇偶校验,它是将要发送的整个信息块分为定长p位的若干段(比如说q段),每段后面按"1"的个数为奇数或偶数的规律加上一位奇偶位,如图2.19所示。各位信息(I11,I21,…,Ipl,I12,…,Ipq)中,每p位构成一段(即图中的一列),共有q段(即共有q列〉。每段加上一位奇偶校验冗余位,即图中的rio编码规则为
注意:此间的"+"指的是模二加,也即异或运算。
图中箭头给出了串行发送的顺序,即逐位先后次序为I11,I21,…,Ip1,r1,I12,…,Ipa,r2,…,儿,…,I间,rq。在编码和校验过程中,用硬件方法或软件方法很容易实现上述连续半加运算,而且可以边发送边产生冗余位;同样,在接收端也可边接收边进行校验后去掉校验位。
垂直奇偶校验方法的编码效率为R=p/(p+1)。通常,取一个字符的代码为一个信息段,这种垂直奇偶校验有时也称为字符奇偶校验。例如,在8位字符代码(即用8位二进制数位表示一个字符)中,p=8,编码效率便为8/9。
垂直奇偶校验方法能检测出每列中的所有奇数位错,但检测不出偶数位的错。对于突发错误来说,奇数位错与偶数位错的发生概率接近于相等,因而对差错的漏检率接近于1/2。
水平奇偶校验
为了降低对突发错误的漏检率,可以采用水平奇偶校验方法。水平奇偶校验又称为横向奇偶校验,它是对各个信息段的相应位横向进行编码,产生一个奇偶校验冗余位,如图2.20所示,编码规则为
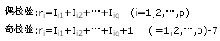 若每个信息段就是一个字符的话,这里的q就是发送的信息块中的字符数。
若每个信息段就是一个字符的话,这里的q就是发送的信息块中的字符数。
水平奇偶校验的编码效率为R=q/(q+1)。
水平奇偶校验不但可以检测出各段同一位上的奇数位错,而且还能检测出突发长度≦p的所有突发错误,因为按发送顺序从图2.20中可见,突发长度≦p的突发错误必然分布在不同的行中,且每行一位,所以可以检查出差错,他的漏检率比垂直奇偶校验方法低。但是实现水平奇偶校验码时,不论是采用硬件还是软件方法,都不能在发送过程中产生奇偶校验冗余位边插入发送,而必须等待要发送的全部信息块到齐后,才能计算冗余位,也就是一定.要使用数据缓冲器,因此它的编码和检测实现起来都要复杂一些。
水平垂直奇偶校验
同时进行水平奇偶校验和垂直奇偶校验就构成水平垂直奇偶校验,也称为纵横奇偶校实验,如图2.21所示。若水平垂直都采用偶校验,则
水平垂直奇偶校验的编码效率为R=pq/[(p+1)(q+1)]。.
水平垂直奇偶校验能检测出所有3位或3位以下的错误(因为此时至少在某一行或某一'列上有一位错)、奇数位错、突发长度<=p+1的突发错以及很大一部分偶数位错。测量表.明,这种方式的编码可使误码率降至原误码率的百分之一到万分之一。
水平垂直奇偶校验不仅可检错,还可用来纠正部分差错。例如数据块中仅存在1位错'时,便能确定错码的位置就在某行和某列的交叉处,从而可以纠正它。
原理
奇偶校验码是 奇校验码和偶校验码的统称,是一种最基本的检错码。它是由n-1位信息元和1位校验元组成,可以表示成为(n,n-1)。如果是奇校验码,在附加上一个校验元以后,码长为n的码字中"1"的个数为奇数个;如果是偶校验码,在附加上一个校验元以后,码长为n的码字中"1"的个数为偶数个。设:如果一个偶校验码的码字用A=[an-1,an-2,…,a1,a0]表示,则:(1) 式中 为校验元,"+"为模二和(以后也这样表示,请注意)。式(1)通常被称为校验方程。利用式(1),由信息元即可求出校验元。另外,如果发生单个(或奇数个)错误,就会破坏这个关系式,因此通过该式能检测码字中是否发生了单个或奇数个错误。




