二分查找

二分查找图解

 

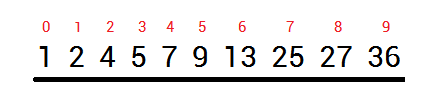
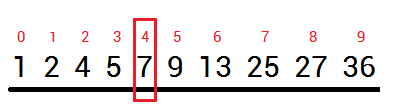
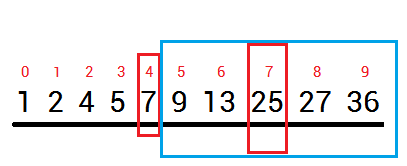
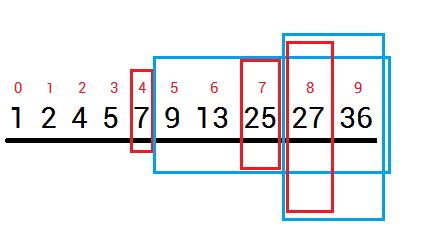
第一类： 查找等于目标值的数

比如我们有数组 [2, 4, 5, 6, 9]，target = 6，那么我们可以写出二分查找法的代码如下：

int find(vector<int> &nums, int target)
{
  int left = 0, right = nums.size() - 1;
  while (left <= right)
  {
    int mid = left + (right - left) / 2;
    if (nums[mid] == target)
      return mid;
    else if (nums[mid] < target)
      left = mid + 1;
    else
      right = mid - 1;
  }
  return -1;
}

 

第二类： 查找第一个不小于目标值的数

这是比较常见的一类，因为我们要查找的目标值不一定会在数组中出现，也有可能是跟目标值相等的数在数组中并不唯一，而是有多个，那么这种情况下 nums[mid] == target 这条判断语句就没有必要存在。比如在数组 [2, 4, 5, 6, 9] 中查找数字3，就会返回数字4的位置；在数组 [0, 1, 1, 1, 1] 中查找数字1，就会返回第一个数字1的位置。我们可以使用如下代码：

int find(vector<int> &nums, int target)
{
  int left = 0, right = nums.size();
  while (left < right)
  {
    int mid = left + (right - left) / 2;
    if (nums[mid] >= target)
      right = mid;
    else
      left = mid + 1;
  }
  return right;
}

 

第三类： 查找第一个大于目标值的数，可变形为查找最后一个不大于目标值的数

这一类也比较常见，尤其是查找第一个大于目标值的数，在 C++ 的 STL 也有专门的函数 upper_bound，这里跟上面的那种情况的写法上很相似，只需要添加一个等号，将之前的 nums[mid] < target 变成 nums[mid] <= target，就这一个小小的变化，其实直接就改变了搜索的方向，使得在数组中有很多跟目标值相同的数字存在的情况下，返回最后一个相同的数字的下一个位置。比如在数组 [2, 4, 5, 6, 9] 中查找数字3，还是返回数字4的位置，这跟上面那查找方式返回的结果相同，因为数字4在此数组中既是第一个不小于目标值3的数，也是第一个大于目标值3的数，所以 make sense；在数组 [0, 1, 1, 1, 1] 中查找数字1，就会返回坐标5，通过对比返回的坐标和数组的长度，我们就知道是否存在这样一个大于目标值的数。参见下面的代码：

int find(vector<int> &nums, int target)
{
  int left = 0, right = nums.size();
  while (left < right)
  {
    int mid = left + (right - left) / 2;
    if (nums[mid] <= target)
      left = mid + 1;
    else
      right = mid;
  }
  return right;
}

参考资料

1. LeetCode Binary Search Summary 二分搜索法小结