【数据结构与算法】堆排序
堆排序
作为选择排序的改进版，堆排序可以把每一趟元素的比较结果保存下来，以便我们在选择最小/大元素时对已经比较过的元素做出相应的调整。堆排序是一种树形选择排序，在排序过程中可以把元素看成是一颗完全二叉树，每个节点都大（小）于它的两个子节点 。
- 当每个节点都大于等于它的两个子节点时，就称为大顶堆，也叫堆有序；
- 当每个节点都小于等于它的两个子节点时，就称为小顶堆。
大顶堆 小顶堆
算法思想(以大顶堆为例)：
- 将长度为n的待排序的数组进行堆有序化构造成一个大顶堆
- 将根节点与尾节点交换并输出此时的尾节点
- 将剩余的n -1个节点重新进行堆有序化
- 重复步骤2，步骤3直至构造成一个有序序列
构造堆
假设待排序数组为[20,50,10,30,70,20,80]
在构造有序堆时，我们开始只需要扫描一半的元素（n/2-1 ~ 0）即可，为什么?
因为0 ~(n/2-1)的节点才有子节点，如图1，n=8, (n/2-1) = 3 即0、1、2、3、4这个四个节点才有子节点。
（图1：初始状态）
第一次for循环将节点3和它的子节点7、8的元素进行比较，最大者作为父节点（即元素60作为父节点）【红色表示交换后的状态】
第二次for循环将节点2和它的子节点5 6的元素进行比较，最大者为父节点（元素80作为父节点）
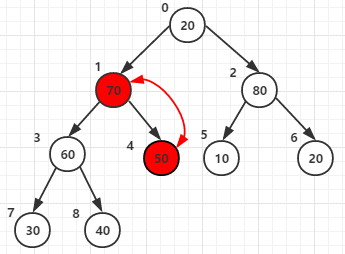
第三次for循环将节点1和它的子节点3、4的元素进行比较，最大者为父节点（元素70作为父节点）
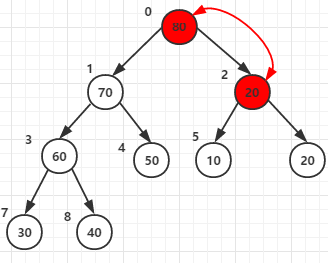
第四次for循环将节点0和它的子节点1、2的元素进行比较，最大者为父节点（元素80作为父节点）
（注意这里，元素20和元素80交换后, 20所在的节点还有子节点，所以还要再和它的子节点5 6的元素进行比较，这就是28行代码 i = j 的原因）
至此有序堆已经构造好了！如下图：
调整堆
下面进行while循环
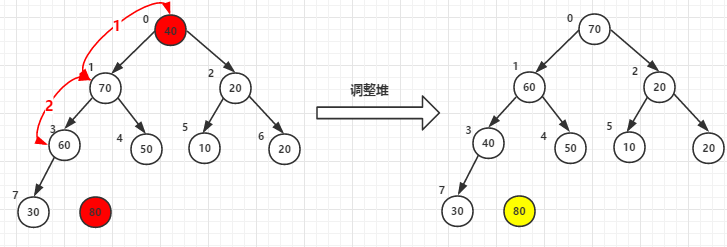
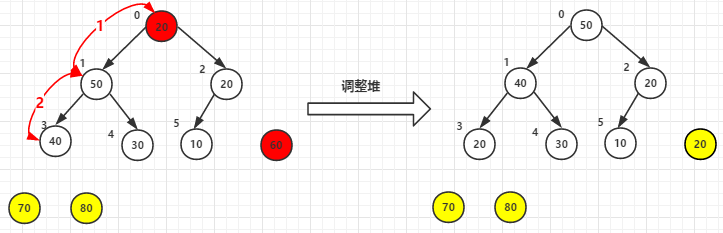
（1）堆顶元素80和尾40交换后-->调整堆
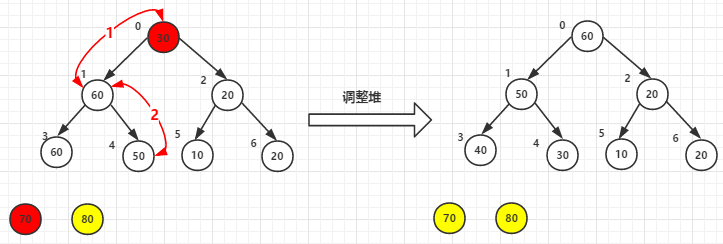
（2）堆顶元素70和尾30交换后-->调整堆
（3）堆顶元素60尾元素20交换后-->调整堆
（4）其他依次类推，最终已排好序的元素如下：
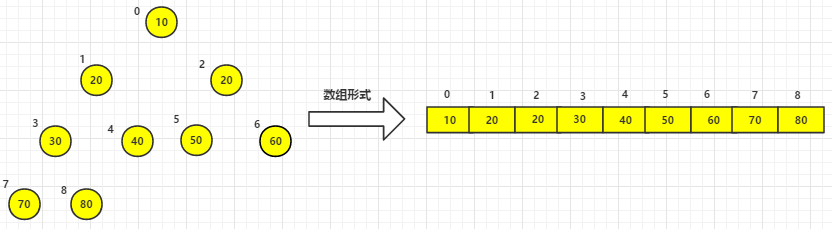
代码实现：
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
void heapAdjust(vector<int>& arr, int i, int len)
{
int left, right, j;
while ((left = 2 * i + 1) <= len) //判断当前父节点有无左节点(即有无孩子节点，left为左节点)
{
right = left + 1; //右节点
j = left; //j指针指向左节点
if (right <= len && arr[left] < arr[right]) //右节点大于左节点
j++; //当前把"指针"指向右节点
//将父节点与孩子节点交换（如果上面if为真，则arr[j]为右节点，如果为假arr[j]则为左节点）
if (arr[i] < arr[j])
swap(arr[i], arr[j]);
else //说明比孩子节点都大，直接跳出循环语句
break;
i = j;
}
}
void heapSort(vector<int> &arr)
{
int len = arr.size() - 1;
for (int i = len / 2 - 1; i >= 0; i--)
heapAdjust(arr, i, len);
while (len >= 0)
{
swap(arr[0], arr[len--]); //将堆顶元素与尾节点交换后，长度减1，尾元素最大
heapAdjust(arr, 0, len); //再次对堆进行调整
}
}
int main()
{
vector<int> vec;
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
int a;
cin >> a;
vec.push_back(a);
}
heapSort(vec);
cout << "排序后：";
for (auto c : vec)
cout << c << " ";
return 0;
}
