paxos算法
paxos算法解析
阅读论文 《Paxos Made Simple》

选定提案的最简单方式就是只允许一个accpetor存在。Proposer发送提案给accpetor,Acceptor会选择它接收到的第一个提案作为被选定的提案。尽管简单,但是这个解决方式却很难让人满意,因为如果accpetor出错,那么整个系统就无法工作了。
因此,应该选择其他的方式。比如我们用多个accpetor来避免一个accpetor时的单点问题。现在,Proposer向一个Acceptor集合发送提案,某个Acceptor可能会通过(accept)这个提案。当有足够多的Acceptor通过(accept)它的时候,我们就可以认为这个提案被选定了。什么是足够多呢?为了能确保只有一个提案被选定,我们可以让这个集合大的可以包含Acceptor集合中的多数成员。因为任何两个多数集至少有一个公共成员,如果我们再规定一个Acceptor最多只能通过一个提案,那么就能保证只有一个提案被选定(这是对于很多论文都研究过的majority的一个简单的应用 [3] )。
在没有失败和消息丢失的情况下,如果我们希望即使在只有一个提案被提出的情况下,仍然可以选出一个提案来,这就暗示了如下这个需求:
P1 . 一个Acceptor必须通过(accept)它收到的第一个提案。
但是这个需求引出了另外一个问题。如果有多个提案被不同的Proposers同时提出,这可能会导致虽然每个Acceptor都通过了一个提案,但是没有一个提案是由多数人都通过的。即使是只有两个提案,如果每个都被差不多一半的Acceptors通过了,此时即使只有一个Acceptor出错都可能使得无法确定该选定哪个提案。 [§]译注
P1 再加上一个提案被选定需要由半数以上的Acceptor通过的需求暗示着一个Acceptor必须能够通过(accept)不止一个提案。我们为每个提案设定一个编号来记录一个Acceptor通过的那些提案。为了避免混淆,需要保证不同的提案具有不同的编号。如何实现这种保证取决于实现,目前我们假设已经提供了这种保证。当一个具有某value值的提案被半数以上的Acceptor通过后,我们就认为该value被选定了。此时我们也认为该提案被选定了。 [¶]译注
我们允许多个提案被选定,但是我们必须要保证所有被选定的提案都具有相同的value值。在提案编号上规约,它需要保证:
P2 . 如果具有value值v的提案被选定(chosen)了,那么所有比它编号更高的被选定的提案的value值也必须是 v 。
因为编号是全序的,条件 P2 就保证了只有一个value值被选定的这一关键安全性属性。
被选定的提案,首先必须被至少一个Acceptor通过,因此我们可以通过满足如下条件来满足 P2 :
P2 a. 如果具有value值 v 的提案被选定(chosen)了,那么所有比它编号更高的被Acceptor通过的提案的value值也必须是 v。
我们仍然需要 P1 来保证提案会被选定。但是因为通信是异步的,一个提案可能会在某个Acceptor c 还未收到任何提案时就被选定了。假设一个新的Proposer苏醒了,然后产生了一个具有另一个value值的更高编号的提案,根据 P1 ,就需要 c 通过这个提案,但是这与 P2 a 矛盾。因此如果要同时满足 P1 和 P2 a ,需要对 P2a 进行强化:
P2 b. 如果具有value值v的提案被选定,那么所有比它编号更高的被Proposer提出的提案的value值也必须是 v 。
一个提案被Acceptor通过之前肯定要由某个Proposer提出,因此 P2 b 就隐含了 P2 a ,进而隐含了 P2 。
为了发现如何保证 P2 b ,我们来看看如何证明它成立。我们假设某个具有编号m和value值v的提案被选定了,需要证明具有编号 n(n > m) 的提案都具有value值 v 。我们可以通过对 n 使用归纳法来简化证明,这样我们就可以在额外的假设下——即编号在 m..(n-1) 之间的提案具有value值 v ,来证明编号为n的提案具有value值 v 。因为编号为m的提案已经被选定了,这意味着肯定存在一个由半数以上的Acceptor组成的集合 C , C 中的每个Acceptor都通过了这个提案。再结合归纳假设, m 被选定意味着:
C 中的每个Acceptor都通过了一个编号在 m..n-1 之间的提案,每个编号在 m..(n-1) 之间的被Acceptor通过的提案都具有value值 v 。
因为任何包含半数以上的Acceptor的集合S都至少包含 C 中的一个成员,我们可以通过维护如下不变性就可以保证编号为n的提案具有value v :
P2 c. 对于任意的 n 和 v ,如果编号为 n 和value值为 v 的提案被提出,那么肯定存在一个由半数以上的Acceptor组成的集合 S ,可以满足条件 a) 或者 b) 中的一个:
- S 中不存在任何的Acceptor通过过编号小于 n 的提案
- v 是 S 中所有Acceptor通过的编号小于 n 的具有最大编号的提案的value值。
通过维护 P2 c 我们就可以保证 P2 b 了。 [#]译注
为了维护 P2 c 的不变性,一个Proposer在产生编号为 n 的提案时,必须要知道某一个将要或已经被半数以上Acceptor通过的编号小于 n 的最大编号的提案。获取那些已经被通过的提案很简单,但是预测未来会被通过的那些却很困难。在这里,为了避免让Proposer去预测未来,我们通过限定不会有那样的通过情况来控制它。换句话说,Proposer会请求Acceptors不要再通过任何编号小于 n 的提案。这就导致了如下的提案生成算法:
- Proposer选择一个新的提案编号 n ,然后向某个Acceptors集合的成员发送请求,要求Acceptor做出如下回应:
- 保证不再通过任何编号小于 n 的提案
- 当前它已经通过的编号小于 n 的最大编号的提案,如果存在的话。
我们把这样的一个请求称为编号为 n 的prepare请求。
- 如果Proposer收到了来自半数以上的Acceptor的响应结果,那么它就可以产生编号为 n ,value值为 v 的提案,这里 v 是所有响应中编号最大的提案的value值,如果响应中不包含任何的提案那么这个值就可以由Proposer任意选择。
Proposer通过向某个Acceptors集合发送需要被通过的提案请求来产生一个提案(此时的Acceptors集合不一定是响应前一请求的那个Acceptors集合)。我们称此请求为 accept 请求。
目前我们描述了Proposer端的算法,Acceptor端是怎样的呢?它可能会收到来自Proposer端的两种请求:prepare请求和accept请求。Acceptor可以忽略任何请求而不用担心破坏其算法的安全性。因此我们只需要说明它在什么情况下可以对一个请求做出响应。它可以在任何时候响应一个prepare请求,对于一个accept请求,只要在它未违反现有承诺的情况下才能响应一个accept请求(通过对应的提案)。换句话说:
P1 a. 一个Acceptor可以接受一个编号为 n 的提案,只要它还未响应任何编号大于 n 的prepare请求。
可以看出 P1 a 蕴含了 P1 。
我们现在就获得一个满足安全性需求的提案选定算法—假设编号唯一的情况下。再做一些小的优化就得到了最终的算法。
假设一个Acceptor收到了一个编号为 n 的prepare请求,但是它已经对编号大于 n 的prepare请求做出了响应,因此它肯定不会再通过任何新的编号为n的提案,那么它就没有必要对这个请求做出响应,因为它肯定不会通过编号为 n 的提案,因此我们会让Acceptor忽略这样的prepare请求。我们也会让它忽略那些它已经通过的提案的prepare请求。
通过这个优化,Acceptor只需要记住它已经通过的最大编号的提案以及它已经做出prepare请求响应的最大编号的提案的编号。因为必须要保证 P1 c 的不变性即使在出错的情况下,Acceptor必须记住这些信息即使是在出错或者重启的情况下。Proposer可以总是可以丢弃提案以及它所有的信息—只要它可以保证不会产生具有相同编号的提案即可。
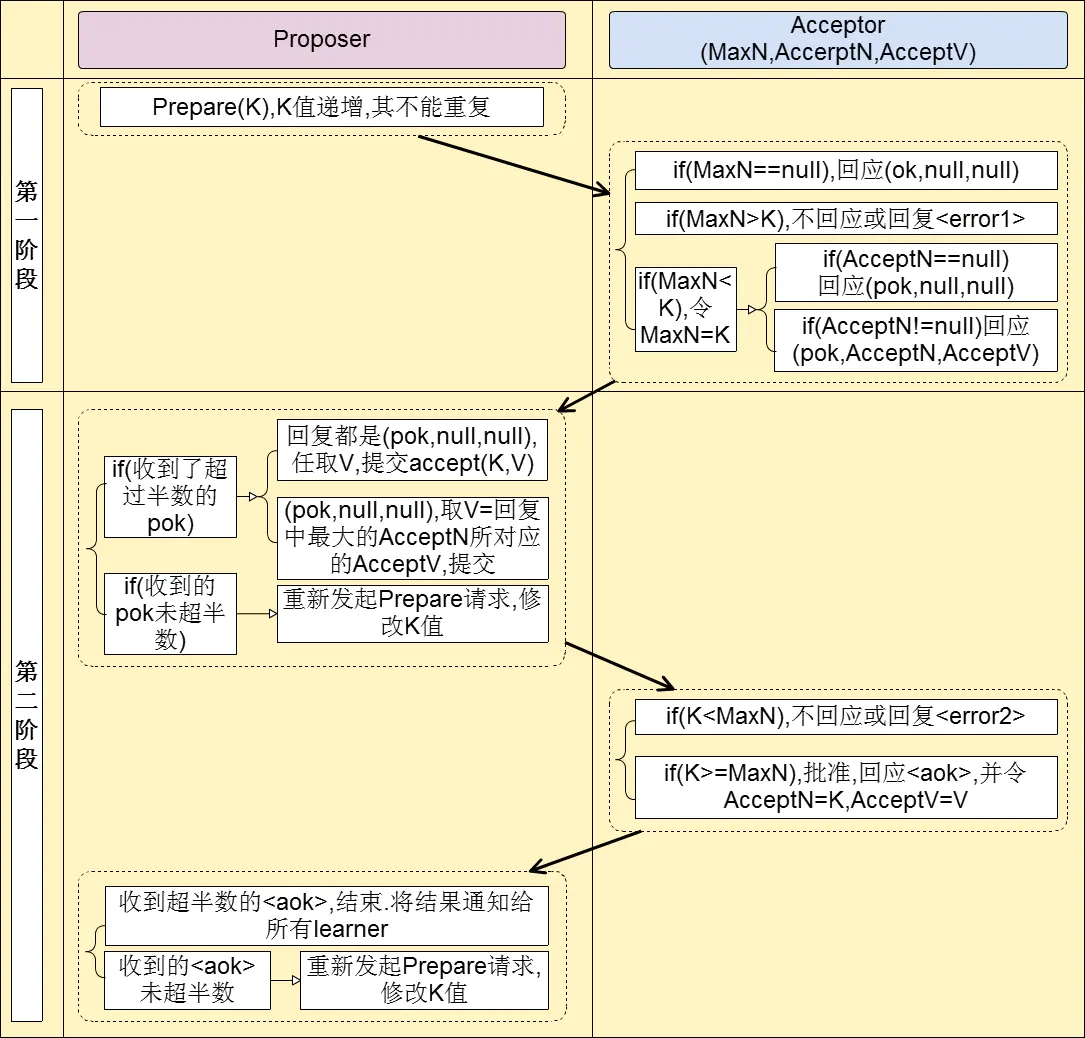
将Proposer和Acceptor放在一块,我们可以得到算法的如下两阶段执行过程:
Phase 1.
- Proposer选择一个提案编号 n ,然后向Acceptors的某个majority集合的成员发送编号为 n 的prepare请求。
- 如果一个Acceptor收到一个编号为 n 的prepare请求,且 n 大于它已经响应的所有prepare请求的编号,那么它就会保证不会再通过(accept)任何编号小于 n 的提案,同时将它已经通过的最大编号的提案(如果存在的话)作为响应。
Phase 2.
- 如果Proposer收到来自半数以上的Acceptor对于它的prepare请求(编号为 n )的响应,那么它就会发送一个针对编号为 n ,value值为 v 的提案的accept请求给Acceptors,在这里 v 是收到的响应中编号最大的提案的值,如果响应中不包含提案,那么它就是任意值。
- 如果Acceptor收到一个针对编号 n 的提案的accept请求,只要它还未对编号大于 n 的prepare请求作出响应,它就可以通过这个提案。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号