【数据结构与算法】归并排序算法

 归并排序算法

1. 分阶段：

 

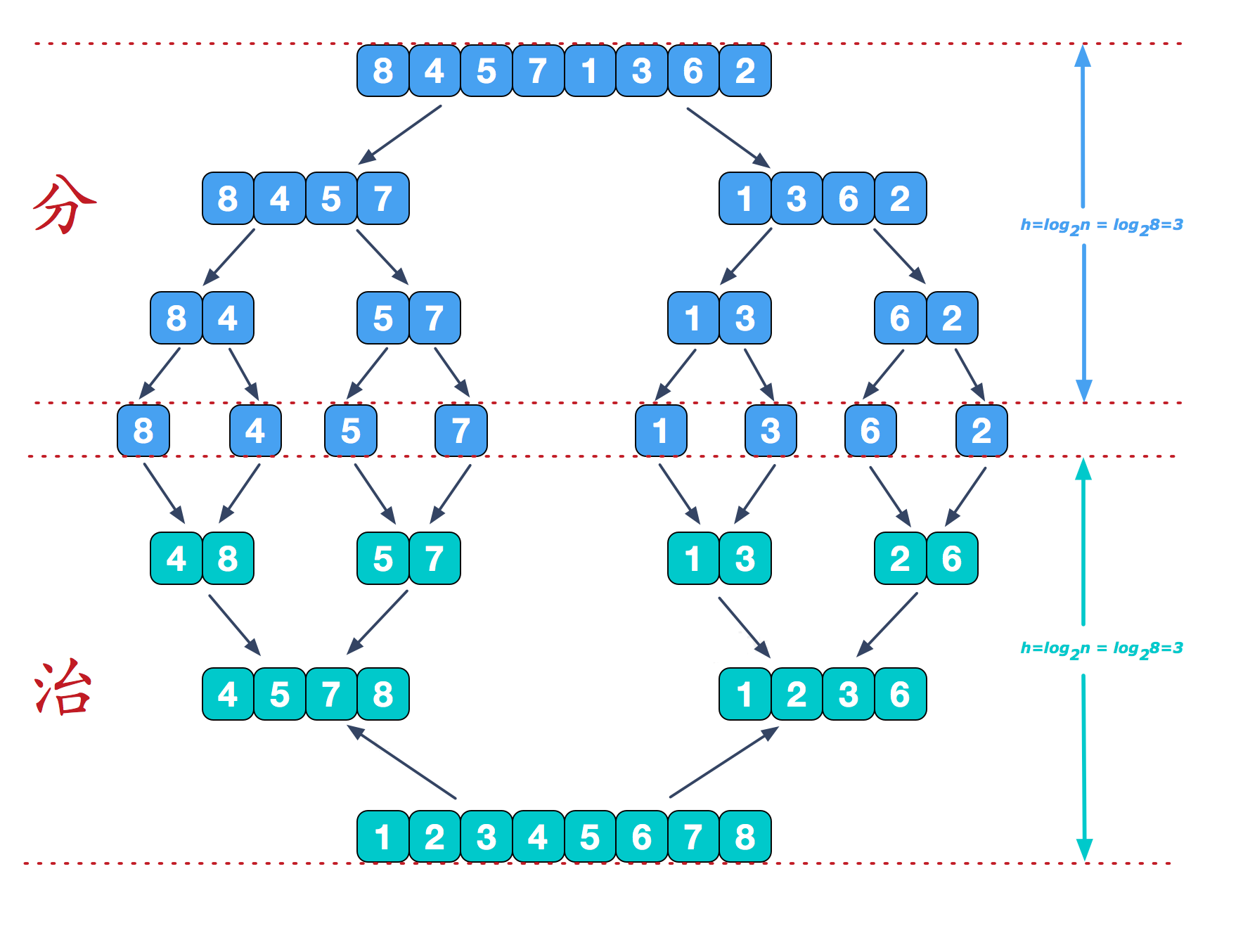
 可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为logn。

2. 治阶段：

再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1, 2, 3, 4, 5, 6, 7, 8]，来看下实现步骤。

 

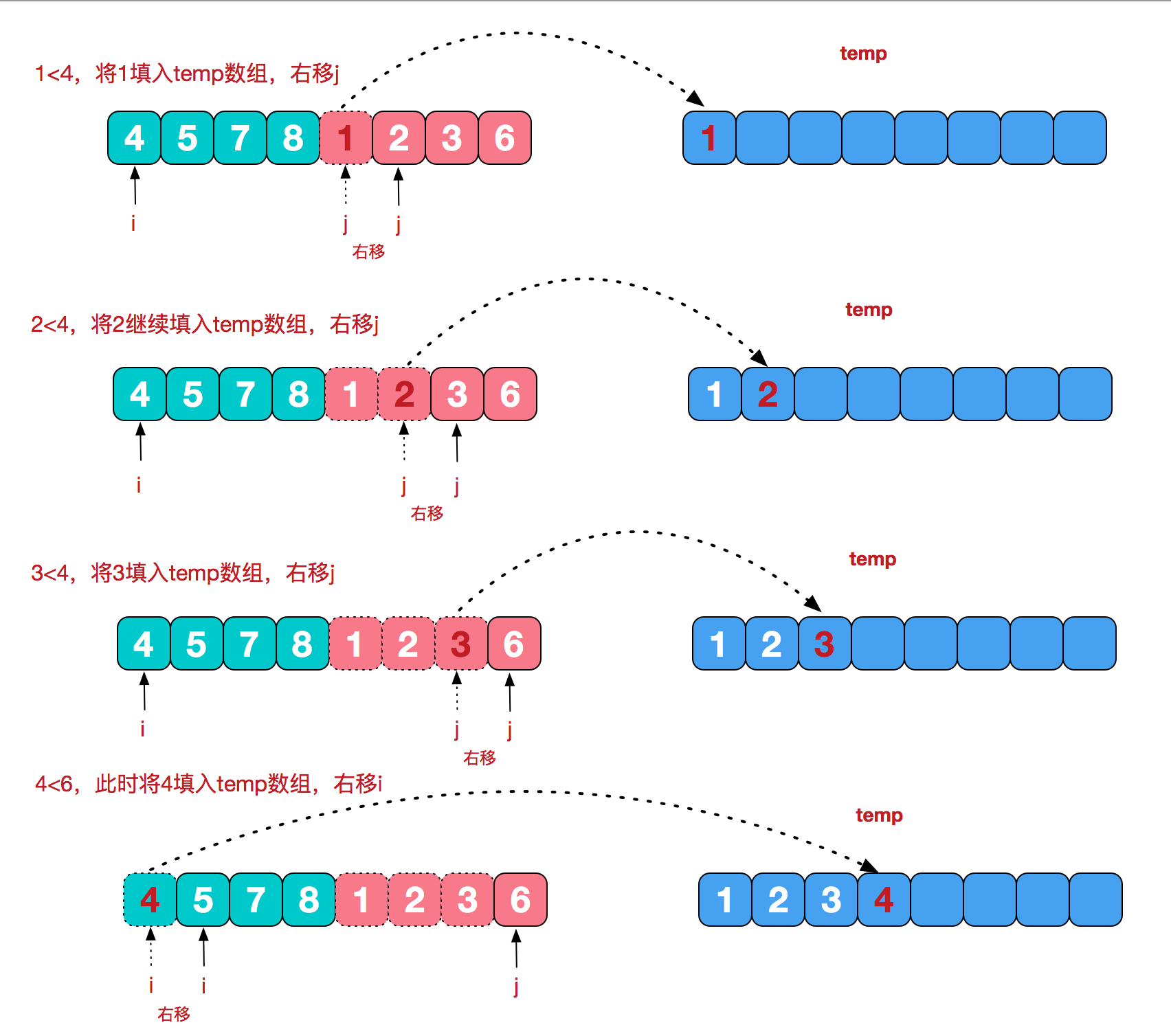
 代码实现：

#include <iostream>
#include <vector>
using namespace std;
 
void merge(vector<int>& data, int left, int mid, int right)
{
    vector<int> temp(data.size());
    int i = left;                    // i是第一段序列的下标
    int j = mid + 1;                 // j是第二段序列的下标
    int k = 0;                       // j是第二段序列的下标
    while (i <= mid && j <= right)   // 扫描第一段和第二段序列，直到有一个扫描结束
    {
        if (data[i] <= data[j])
            temp[k++] = data[i++];
        else
            temp[k++] = data[j++];
    }
    while (i <= mid)                // 若第一段序列还没扫描完，将其全部复制到合并序列
        temp[k++] = data[i++];
    while (j <= right)              // 若第二段序列还没扫描完，将其全部复制到合并序
        temp[k++] = data[j++];
    k = 0;
    while (left <= right)           // 将合并序列复制到原始序列中
    {
        data[left++] = temp[k++];
    } 
}
 
void mergesort(vector<int> &data, int left, int right)
{
    if (left < right)
    {
        int mid = (left + right) / 2;
        mergesort(data, left, mid);
        mergesort(data, mid + 1, right);
        merge(data, left, mid, right);
    }
}
 
int main()
{
    int n;
    cin >> n;
    vector<int> data;
    for (int i = 0; i < n; ++i)
    {
        int a;
        cin >> a;
        data.push_back(a);
    }
    mergesort(data, 0, data.size() - 1);
    for (auto c : data)
        cout << c << " ";
    return 0;
}

 

经典例题：

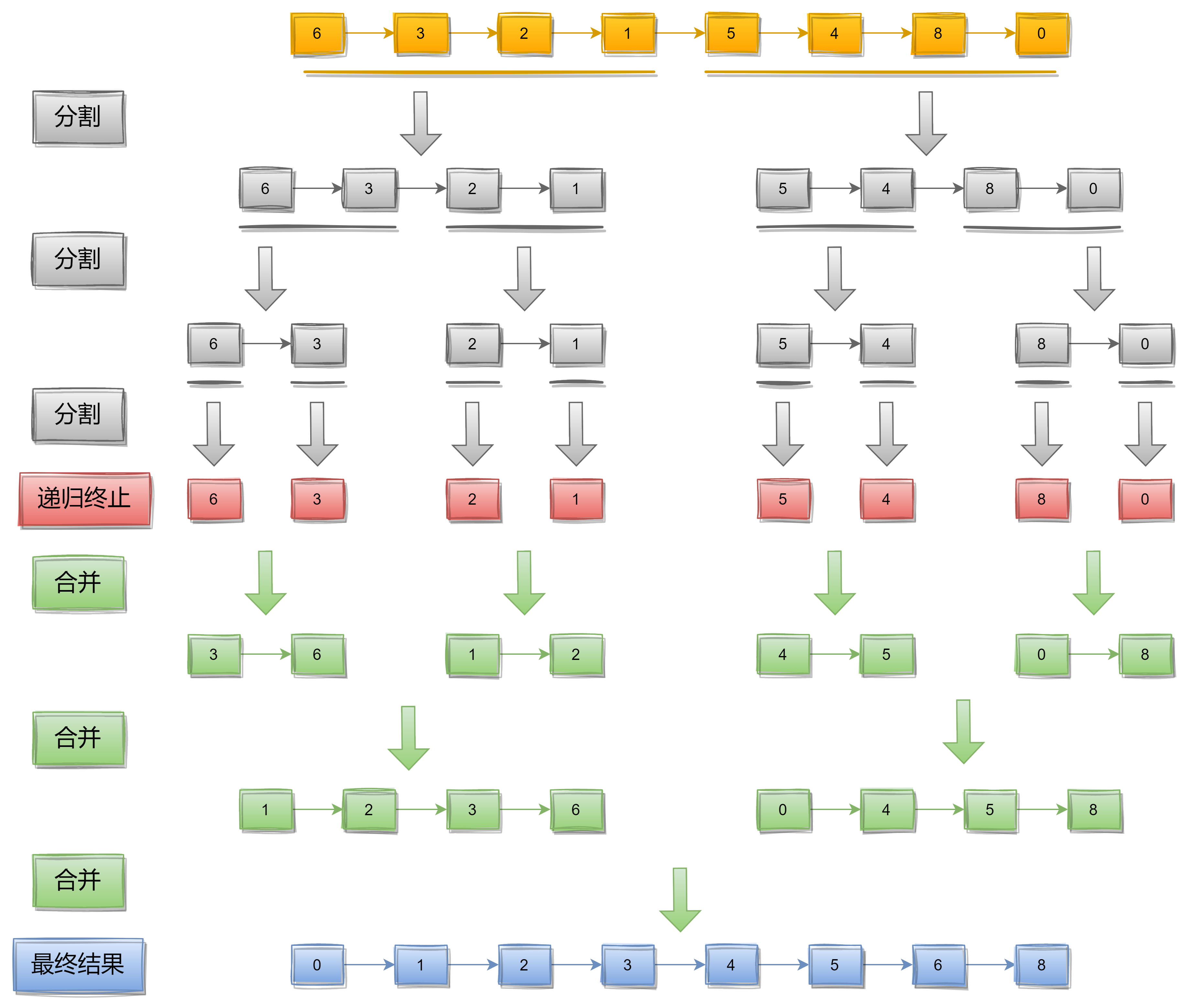
想一想看，如果给你两个已经排好序的链表，那么只需要对这两个已经排好序的链表按顺序进行合并就能得到一个有序的链表，所以‘子问题’意思是把对子链表进行排序。

‘归并排序’中的并字其实就代表对两个子链表进行合并，那么归字是什么意思呢？这道题可以使用递归的方式对子链表进行排序，所以归暗示着使用递归的方式对子问题进行求解，也就是使用递归来对子链表进行排序。

整体思路大概如下

把无序链表head分成两个子链表，分别为headA和headB。
使用递归的方式对headA和headB这两个子链表进行排序。
按顺序对headA和headB这两个子链表进行合并。

作者：glodknife
链接：https://leetcode-cn.com/problems/sort-list/solution/jin-dao-gui-bing-pai-xu-kan-tu-jiu-dong-wz6y1/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

参考资料

1. 【金刀】归并排序~看图就懂