树链剖分
模板：洛谷P3384
看到题目，是不是觉得似曾相识？
我们把这道题拆分一下（操作3和4暂时不管）
如果只有操作1，你会想到，这可以用树上差分来维护
如果只有操作2，树上倍增lca大水题
那么把两个结合起来就是我们现在看到的这道题目...
怎么做呢？
我们想，这道题跟线段树版题又挺像的，只是变到了树上
那么是不是可以把这棵树拆成许多条链，每条链用线段树（或其他数据结构）进行维护，最后再把所有经过的链的答案加起来呢？
这就是树链剖分。
算一下，单次修改或查询的时间复杂度为O(k*logn)，k是经过的链的条数
又一个问题来了：怎么去拆分这棵树，使得k尽可能小呢？
这里介绍轻重链拆分法，它可以保证从树上一点到另一点经过的链的条数不超过logn条，所以单次最多O((logn)^2)
为啥不超过logn条呢？
首先明确几个名词：
重儿子：父亲节点的所有儿子中子树结点数目最多（size最大）的结点；
轻儿子：父亲节点中除了重儿子以外的儿子；
重边：父亲结点和重儿子连成的边；
轻边：父亲节点和轻儿子连成的边；
重链：由多条重边连接而成的路径；
轻链：由多条轻边连接而成的路径；
首先，如果u->v(dep[u]<dep[v])是一条轻边，那么一定有size[v]<=size[u]/2。否则v就一定是u的重儿子，这与先前假设的轻边矛盾。
然后，对于任意一条从根到一点的路径，因为我们发现了上述结论，所以经过的轻边必不超过logn条（最坏情况下，对n不停的除以2），即经过的链不超过logn条。
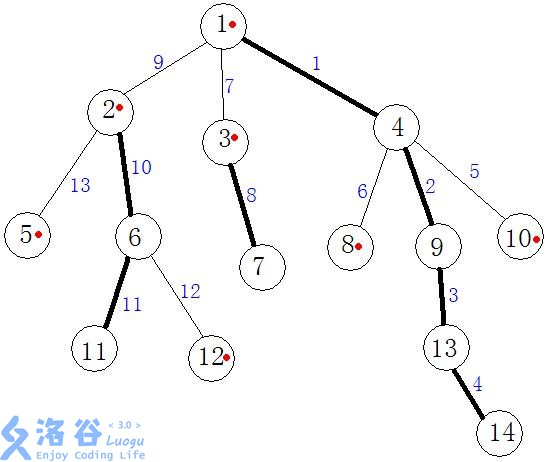
上图中加粗的边就是重边
图中所有的重链就是我们分出来的链，特别的，没有被重链覆盖的单个节点也看做一条链来维护
因为链与链之间互不干扰，所以实际上只需要建一颗线段树就可以维护所有链了！
这涉及到线段树中节点序号的问题。我们需要让重链上的节点的新序号是连续的，这样才能用线段树维护
我们将会使用2遍dfs完成对这棵树的拆分
第一遍dfs，处理出每个节点的父亲(prt)、深度(dep)、大小(size)，以及他的重儿子(son)
第二遍dfs，处理每个节点所在重链的顶部节点编号(top)，还有在线段树中的新编号(rk)。遍历时优先进入重儿子，保证重链编号的连续。
这样就拆分完了。其实树链剖分的主体并不长。
拆分完了，就该处理修改和查询了。以查询为例
比较两个节点的top的深度，选择深度较大的那一个节点，上跳到它top的父亲那里去。如果top是根节点就不跳了
在这个过程中把上跳的这一段用线段树求和，加到ans里。
循环往复，直到两个节点的top相同，说明他们在同一条重链里了，此时在加入他们之间节点的和，bingo！
修改和查询差不多，就不多说了
回头看操作3和操作4，对子树的统一操作，这不更简单吗？
我们的遍历是保证了同一子树内的dfs序是连续的，所以直接对线段树里的rk[id]~(rk[id]+size[id]-1)操作就行了
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<ctime> #include<cstdlib> #include<queue> using namespace std; struct SegTree{//线段树 struct Node{ long long l,r,val,lazy; }tree[400000]; long long size; void build(long long id,long long l,long long r){ tree[id]=(Node){l,r,0,0}; if(l==r) return ; long long mid=(l+r)/2; build(id*2,l,mid); build(id*2+1,mid+1,r); } void lazydown(long long id){ long long lc=id*2,rc=id*2+1,lazy=tree[id].lazy; tree[lc].lazy+=lazy; tree[lc].val+=(tree[lc].r-tree[lc].l+1)*lazy; tree[rc].lazy+=lazy; tree[rc].val+=(tree[rc].r-tree[rc].l+1)*lazy; tree[id].lazy=0; } long long al,ar,aval; void update(long long id){ long long l=tree[id].l,r=tree[id].r; if(al<=l&&r<=ar){ tree[id].lazy+=aval; tree[id].val+=(r-l+1)*aval; return ; } if(tree[id].lazy!=0) lazydown(id); long long mid=(l+r)/2; if(al<=mid) update(id*2); if(ar>mid) update(id*2+1); tree[id].val=tree[id*2].val+tree[id*2+1].val; } void afo(long long id){//别问我这个函数名是什么鬼 long long l=tree[id].l,r=tree[id].r; if(al<=l&&r<=ar){ aval+=tree[id].val; return ; } if(tree[id].lazy!=0) lazydown(id); long long mid=(l+r)/2; if(al<=mid) afo(id*2); if(ar>mid) afo(id*2+1); } //for user void init(long long mys){ size=mys; build(1,1,size); } void change(long long l,long long r,long long val){ al=l;ar=r;aval=val; update(1); } long long ask(long long l,long long r){ al=l;ar=r;aval=0; afo(1); return aval; } }; long long n,qn,root,MOD; struct star{//链式前向星存树 long long u,v; }edge[400000]; long long last[400000],nxt[400000],m; void addedge(long long u,long long v){ m++; edge[m]=(star){u,v}; nxt[m]=last[u]; last[u]=m; } long long prt[400000],dep[400000],size[400000], son[400000],top[400000],rk[400000],rkn; void dfs1(long long id,long long fa,long long d){//第一遍dfs，处理prt,dep,size,son prt[id]=fa; dep[id]=d; size[id]=1; long long fat=-1; for(long long i=last[id];i!=-1;i=nxt[i]){ long long to=edge[i].v; if(to==fa) continue; dfs1(to,id,d+1); size[id]+=size[to]; if(fat==-1) fat=to; else if(size[to]>size[fat]) fat=to; } son[id]=fat; } void dfs2(long long id,long long tp){//第二遍dfs，处理top,rk rkn++;rk[id]=rkn; top[id]=tp; if(son[id]==-1) return; dfs2(son[id],tp); for(long long i=last[id];i!=-1;i=nxt[i]){ long long to=edge[i].v; if(to==prt[id]||to==son[id]) continue; dfs2(to,to); } } SegTree seg; void change(long long px,long long py,long long val){//操作1 for(;top[px]!=top[py];){ if(dep[top[px]]<dep[top[py]]) swap(px,py);//注意应比较top[px]和top[py]的深度，而不是px和py的深度 long long fx=top[px],fy=top[py]; if(prt[fx]!=-1){//如果top不是根节点 seg.change(rk[fx],rk[px],val); px=prt[fx]; } } if(rk[px]>rk[py]) swap(px,py);//就是这里忘swap了害得我调了1hour seg.change(rk[px],rk[py],val); } long long ask(long long px,long long py){//操作2 long long ans=0; for(;top[px]!=top[py];){ if(dep[top[px]]<dep[top[py]]) swap(px,py); long long fx=top[px],fy=top[py]; if(prt[fx]!=-1){ ans+=seg.ask(rk[fx],rk[px]); px=prt[fx]; } } if(rk[px]>rk[py]) swap(px,py); ans+=seg.ask(rk[px],rk[py]); return ans; } long long stv[400000]; int main(){ cin>>n>>qn>>root>>MOD; seg.init(n); for(long long i=1;i<=n;i++){ scanf("%lld",&stv[i]); } m=0; for(long long i=1;i<=n;i++) last[i]=-1; for(long long i=1;i<=n-1;i++){ long long u,v; scanf("%lld%lld",&u,&v); addedge(u,v); addedge(v,u); } dfs1(root,-1,1); rkn=0; dfs2(root,root); for(long long i=1;i<=n;i++){ seg.change(rk[i],rk[i],stv[i]); } for(long long i=1;i<=qn;i++){ long long type,l,r,val; scanf("%lld",&type); switch(type){ case 1:{ scanf("%lld%lld%lld",&l,&r,&val); change(l,r,val); break; } case 2:{ scanf("%lld%lld",&l,&r); printf("%lld\n",ask(l,r)%MOD); break; } case 3:{ scanf("%lld%lld",&l,&val); r=rk[l]+size[l]-1; l=rk[l]; seg.change(l,r,val); break; } case 4:{ scanf("%lld",&l); r=rk[l]+size[l]-1; l=rk[l]; printf("%lld\n",seg.ask(l,r)%MOD); break; } } } return 0; }
#include<iostream> #include<cstdio> #include<cmath> #include<ctime> #include<algorithm> #include<queue> using namespace std; const int INF=999999999,MXN=500005; int MOD; struct SegTree{ struct Node{ int l,r; int tot,add; int Length(){return r-l+1;} }tr[MXN*4]; int sz; void Pushdown(int x){ if(tr[x].add!=0){ tr[x*2].add+=tr[x].add; tr[x*2+1].add+=tr[x].add; tr[x*2].tot+=tr[x].add*tr[x*2].Length(); tr[x*2+1].tot+=tr[x].add*tr[x*2+1].Length(); } tr[x].add=0; } void Update(int x){tr[x].tot=tr[x*2].tot+tr[x*2+1].tot;} void Build(int x,int l,int r){ tr[x]=(Node){l,r,0,0}; if(l==r) return; int mid=(l+r)/2; Build(x*2,l,mid); Build(x*2+1,mid+1,r); } int al,ar,aval; void Change(int x){ int l=tr[x].l,r=tr[x].r; if(al<=l&&r<=ar){ tr[x].add+=aval; tr[x].tot+=aval*tr[x].Length(); return;} Pushdown(x); int mid=(l+r)/2; if(al<=mid) Change(x*2); if(ar>mid) Change(x*2+1); Update(x); } int Ask(int x){ int l=tr[x].l,r=tr[x].r; if(al<=l&&r<=ar) return tr[x].tot; Pushdown(x); int mid=(l+r)/2,ans=0; if(al<=mid) ans+=Ask(x*2); if(ar>mid) ans+=Ask(x*2+1); return ans; } void Init(int mys){sz=mys;Build(1,1,sz);} void Modify(int l,int r,int val){ if(l>r) return; al=l;ar=r;aval=val; Change(1); } int Query(int l,int r){ if(l>r) return 0; al=l;ar=r; return Ask(1); } }seg; int n,qn,root; //Star int to[MXN],nxt[MXN],last[MXN],en; void addedge(int u,int v){ to[++en]=v; nxt[en]=last[u]; last[u]=en; } int prt[MXN],dep[MXN],size[MXN],son[MXN]; //Tree Dividing void DFS1(int x,int fa,int d){ prt[x]=fa;dep[x]=d; size[x]=1;son[x]=0; for(int i=last[x];i!=0;i=nxt[i]){ int go=to[i];if(go==fa) continue; DFS1(go,x,d+1); size[x]+=size[go]; if(size[go]>size[son[x]]) son[x]=go; } } int top[MXN],rk[MXN],rkn; void DFS2(int x,int tp){ rk[x]=++rkn;top[x]=tp; if(!son[x]) return; DFS2(son[x],tp); for(int i=last[x];i!=0;i=nxt[i]){ int go=to[i]; if(go==prt[x]||go==son[x]) continue; DFS2(go,go); } } void Modify(int x,int y,int val){ while(top[x]!=top[y]){ if(dep[top[x]]<dep[top[y]]) swap(x,y); int fx=top[x]; if(prt[fx]){ seg.Modify(rk[fx],rk[x],val); x=prt[fx]; } } if(dep[x]>dep[y]) swap(x,y); seg.Modify(rk[x],rk[y],val); } int Query(int x,int y){ int ans=0; while(top[x]!=top[y]){ if(dep[top[x]]<dep[top[y]]) swap(x,y); int fx=top[x]; if(prt[fx]){ ans+=seg.Query(rk[fx],rk[x]); x=prt[fx]; } } if(dep[x]>dep[y]) swap(x,y); ans+=seg.Query(rk[x],rk[y]); return ans; } int ptv[MXN]; int main(){ cin>>n>>qn>>root>>MOD; en=0;for(int i=1;i<=n;i++) last[i]=0; seg.Init(n); for(int i=1;i<=n;i++) scanf("%d",&ptv[i]); for(int i=1;i<n;i++){ int u,v;scanf("%d%d",&u,&v); addedge(u,v);addedge(v,u); } prt[0]=dep[0]=size[0]=son[0]=0; DFS1(root,0,1); rkn=0;DFS2(root,root); for(int i=1;i<=n;i++) seg.Modify(rk[i],rk[i],ptv[i]); for(int i=1;i<=qn;i++){ int type;scanf("%d",&type); int u,v,val; switch(type){ case 1:{ scanf("%d%d%d",&u,&v,&val); Modify(u,v,val); break;} case 2:{ scanf("%d%d",&u,&v); printf("%d\n",Query(u,v)%MOD); break;} case 3:{ scanf("%d%d",&u,&val); seg.Modify(rk[u],rk[u]+size[u]-1,val); break;} case 4:{ scanf("%d",&u); printf("%d\n",seg.Query(rk[u],rk[u]+size[u]-1)%MOD); break;} } } return 0; }
LCA也可以用树剖来做。由于不需要打又臭又长的线段树，代码比倍增还短一点
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<queue> using namespace std; int n,m,root; struct star{ int u,v; }edge[1000005]; int last[1000005],nxt[1000005]; void addedge(int u,int v){ m++; edge[m]=(star){u,v}; } void starinit(){ for(int i=1;i<=n;i++) last[i]=-1; for(int i=1;i<=m;i++){ int flag=edge[i].u; nxt[i]=last[flag]; last[flag]=i; } } int size[1000005],prt[1000005],dep[1000005],son[1000005],top[1000005]; void dfs1(int node,int fa,int d){ prt[node]=fa; dep[node]=d; size[node]=1; int mxs=0,mxn=-1; for(int i=last[node];i!=-1;i=nxt[i]){ int to=edge[i].v; if(to!=fa){ dfs1(to,node,d+1); size[node]+=size[to]; if(size[to]>mxs){ mxs=size[to]; mxn=to; } } } son[node]=mxn; } void dfs2(int node,int tp){ top[node]=tp; if(son[node]==-1) return; dfs2(son[node],tp); for(int i=last[node];i!=-1;i=nxt[i]){ int to=edge[i].v; if(to!=prt[node]&&to!=son[node]){ dfs2(to,to); } } } int ask(int px,int py){ for(;top[px]!=top[py];){ int fx=top[px],fy=top[py]; if(dep[fx]<dep[fy]) swap(px,py); px=top[px]; if(prt[px]!=-1) px=prt[px]; } if(dep[px]>dep[py]) swap(px,py); return px; } int main(){ int qn; cin>>n>>qn>>root; m=0; for(int i=1;i<=n-1;i++){ int u,v; scanf("%d%d",&u,&v); addedge(u,v); addedge(v,u); } starinit(); dfs1(root,-1,1); dfs2(root,root); for(int i=1;i<=qn;i++){ int px,py; scanf("%d%d",&px,&py); printf("%d\n",ask(px,py)); } return 0; }
Extra：某毒瘤大版题：loj139 树链剖分
你从未做过的船新操作——树剖换根
施工中...
习题：
国家集训队 旅游 求和+max+min
