Splay
狂肝8h才调对的平衡树...真的巨难调...
洛谷dalao写的极好的详解：https://www.luogu.org/blog/user19027/solution-p3369
然后几乎就不需要我讲了
平衡树这个东西...就是二叉搜索树的升级版，解决了二叉搜索树深度不均的劣势，让树尽可能的“平衡”，也就是深度接近。Splay均摊下来是logn的。
证明好像还扯到了什么奇怪的势能分析啊...不会了
更新信息 Update(x)
信息其实就只有一个啦，维护一下size就行了，等于x的两个儿子节点的size之和加上自己的重复次数num。
void Update(int x){//更新size等数据 int lc=tr[x].ch[0],rc=tr[x].ch[1]; tr[x].sz=tr[lc].sz+tr[rc].sz+tr[x].num; }
旋转 Rotate(x)
几乎是平衡树的通用操作，这是保证树平衡的最基础的操作。
我这里有棵树，有个节点x，它的梦想是打倒剥削它多年的y，翻身当y的爸爸（弥天大雾）
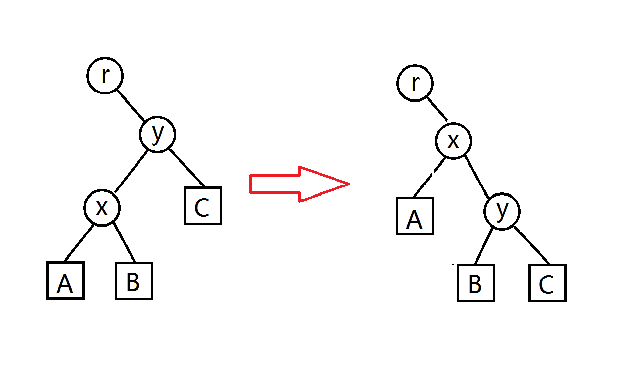
注：圆节点代表单个节点，方节点代表一个节点或一颗子树
但是当爸爸也要按照基本法来呀，二叉搜索树的性质不能被破坏，x当了爸爸后仍然得保证x比A里的数大，比y小。
于是就有了上图的旋转操作。（上图展示的是右旋，左旋就是反过来的过程）
具体怎么实现呢？我们令一个函数Link(a,b,rlt)表示把以rlt的父子关系连接a和b。这个函数将会同时更改a认的父亲和b认的儿子（rlt即a将作为b的左儿子还是右儿子，左为0，右为1）
先暂时不考虑rlt的问题，咱们的旋转操作就是这样滴
Link(b,y) //b认y为父亲，y认b为儿子
Link(y,x) //x跳上来当y爸爸，y也只好认了
Link(x,r) //x认 之前y的爸爸 为爸爸
请自己动手画一画，画出图来就好理解了。
现在考虑rlt的问题。
第一个操作Link(b,y)，对照图来看，关系应该与x、y的关系相同。
第二个操作Link(y,x)，显然关系与先前x、y的关系相反。
第三个操作Link(x,r)，显然关系与先前y、r的关系相同。
上述关系都可以在旋转前确定。
最后，因为改变了节点的父子关系，所以Update一下，这时y已经是x的儿子了，所以先Update(y)，再Update(x)。
这样靠关系确定如何旋转的方式左旋和右旋通用，少打了许多代码 :p
void Link(int x,int fa,bool rlt){//以rlt的父子关系连接x，fa if(x) tr[x].prt=fa; if(fa) tr[fa].ch[rlt]=x; } void Rotate(int x){//旋转，左右旋自适应 int y=tr[x].prt,r=tr[y].prt; bool Rxy=Rlt(x),Ryr=Rlt(y); int b=tr[x].ch[Rxy^1]; Link(b,y,Rxy); Link(y,x,Rxy^1); Link(x,r,Ryr); Update(y);Update(x); }
伸展 Splay(x,to)
这个和算法同名的函数，也是算法的核心。意为将节点x上旋到to这个位置。
有人说：这还不简单，不停Rotate(x)不就完了吗？
其实这个上旋还是有一定的章法的...只不过有些题数据实在太水
比如当我们发现
x和他爸爸fa的关系==fa和fa的爸爸的关系
那我们就先Rotate(fa)，再Rotate(x)。
否则
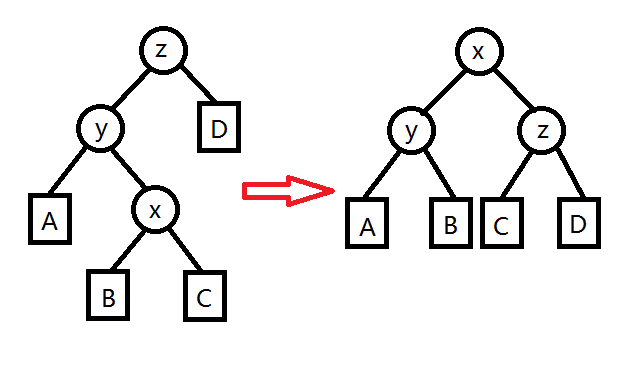
Rotate(x)，Rotate(x)。
建议画图手动模拟一下
为啥这么旋？
保证时间复杂度
玄学.jpg
那么就不停的进行这两个操作，直到到达to的位置。
等等，我怎么知道到底到没到to的位置？等我知道的时候to已经被换下去了呀！
莫慌，我们只需要判断x的爸爸是不是to的爸爸即可，而当我们发现x的爷爷是to的爸爸（即x的爸爸就是to）的时候，我们只进行一次Rotate(x)退出即可。
PS：如果需要记录根，Splay结束后应该更新一下root
void Splay(int x,int to){//将x节点旋至to int tfa=tr[to].prt; while(tr[x].prt!=tfa){//通过to的父亲判断x是否到达 int fa=tr[x].prt; if(tr[fa].prt!=tfa){ if(Rlt(x)==Rlt(fa)) Rotate(fa); else Rotate(x); }Rotate(x); } if(to==root) root=x;//改根 }
插入 Insert(val)
加入一个值为val的数。
没什么好说的，很普通的按照二叉搜索树的方式走下去，因为是新加入数，沿路给每个节点的size++
如果发现val已经有节点在记录了，就给这个节点的重复次数num++
否则走到底了，新建节点，儿子认爸爸，爸爸认儿子，完了。
注意结束后Splay一下保证平衡。[玄学]
（Create函数专门用于初始化新节点的数据，包括值和父节点信息）
void Insert(int val){//插入值为val的节点 if(root==0){root=Create(0,val);return;}//无根 int x=root; while(1){ tr[x].sz++;//沿路更新size if(tr[x].val==val){tr[x].num++;break;}//已有节点，仅num++ bool R=val>tr[x].val; if(!tr[x].ch[R])//走到头 {x=tr[x].ch[R]=Create(x,val);break;}//创建，改儿子 x=tr[x].ch[R]; } Splay(x,root); }
删除 Del(val)
删掉一个值为val的数。
当然是先按二叉搜索树的方法找到这个值为val的节点，因为会删掉其中的数，沿路给每个节点的size--
如果这个节点的重复次数num大于1，那直接num--即可
否则把它Splay到根。
想要删掉现在的根，则需要让它的两个子树重新结合成一颗二叉搜索树。
情况1：如果没有左子树，直接删根，然后右儿子没有爸爸，设为根即可。
情况2：如果有左子树，那就找到左子树中最大的那一个节点（根的前驱），把它Splay到当前根的左儿子去。因为前驱刚好比root小，它又是root的左儿子，所以此时前驱没有右儿子！
把根的右子树接到前驱的右儿子上（Link），删根，前驱没有爸爸，设为根，完事。
完事个锤子！儿子都变了你不Update一下吗？
完了...这次真的完了
void Del(int val){ if(tr[root].ch[0]==0&&tr[root].ch[1]==0&&tr[root].num==1)//如果只剩根节点且只有一个值 {Remove(root);root=0;return;} int x=root; while(x){//找到删除节点 tr[x].sz--;//沿路更新size if(tr[x].val==val) break; x=tr[x].ch[val>tr[x].val]; }if(!x) return;//找不到 if(tr[x].num>1){tr[x].num--;return;}//多于1个，仅num-- Splay(x,root);//旋上根 int lc=tr[x].ch[0],rc=tr[x].ch[1]; if(!lc)//无左子树 {tr[rc].prt=0,Remove(x),root=rc;return;}//右子树为根 int pre=lc; while(tr[pre].ch[1]) pre=tr[pre].ch[1];//找前驱 Splay(pre,lc);//前驱旋到左儿子 Link(rc,pre,1);//右儿子认前驱为父 tr[pre].prt=0,Remove(x),root=pre;//换根三连 Update(pre);//更新前驱（已经是根节点了），删除原点 }
其他操作 GetRank(val)，Kth(rk)，GetPre(val)，GetNxt(val)，...
找数val前有几个数（排名-1），找排名为rk的数，找第一个比val小的数，找第一个比val大的数...
这些都只是利用二叉搜索树的性质解决，比较简单，故不一一讲解。如有需要，参考上方链接。
简单说一下GetRank(val)的实现。
从根向下走，如果要查的val比当前节点的val小，走到左儿子，什么也不做。
如果比它大，给答案加上左儿子的size，再加上当前节点的num，走到右儿子。
最后走到val了或者走到底了，跳出，答案是现成的。
代码包括上面四个操作并给予简单的解释。
int GetRank(int val){//获得某数前有多少个数 int x=root,rk=0; while(x){ int lc=tr[x].ch[0],rc=tr[x].ch[1]; if(val==tr[x].val) {rk+=tr[lc].sz;break;} if(val<tr[x].val) x=lc; else rk+=tr[lc].sz+tr[x].num,x=rc; } if(x) Splay(x,root); return rk; } int Kth(int want){//找第k小的数 int x=root,rk=0;want--; while(x){ int lc=tr[x].ch[0],rc=tr[x].ch[1]; int tmp=rk+tr[lc].sz; if(tmp<=want&&want<tmp+tr[x].num) break;//在这个区间内前头都有tmp个数，注意是给want限制了范围，而不是tmp if(want<tmp) x=lc; else rk=tmp+tr[x].num,x=rc; }if(!x) return 0; Splay(x,root); return tr[x].val; } int GetPre(int val){//获取第一个比val小的数 int x=root,ans=-INF; while(x){//尝试不停向val靠近并使x严格不大于等于val if(val<=tr[x].val) x=tr[x].ch[0]; else ans=max(ans,tr[x].val),x=tr[x].ch[1];//找到最大值 } return ans; } int GetNxt(int val){//获取第一个比val大的数 int x=root,ans=INF; while(x){ if(val<tr[x].val) ans=min(ans,tr[x].val),x=tr[x].ch[0]; else x=tr[x].ch[1]; } return ans; }
总代码：
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<ctime> #include<cstdlib> #include<queue> //#include<windows.h> using namespace std; const int MXN=500005,INF=999999999; struct BST{ struct Node{ int prt,ch[2]; int val,num,sz;//val：值，num：重复次数，sz：管辖节点数目（包含自己） }tr[MXN]; int pn,root; bool Rlt(int x){return tr[tr[x].prt].ch[1]==x;}//获取x和父亲的关系，0=左儿子，1=右儿子 void Update(int x){//更新size等数据 int lc=tr[x].ch[0],rc=tr[x].ch[1]; tr[x].sz=tr[lc].sz+tr[rc].sz+tr[x].num; } void Link(int x,int fa,bool rlt){//以rlt的父子关系连接x，fa if(x) tr[x].prt=fa; if(fa) tr[fa].ch[rlt]=x; } void Rotate(int x){//旋转，左右旋自适应 int y=tr[x].prt,r=tr[y].prt; bool Rxy=Rlt(x),Ryr=Rlt(y); int b=tr[x].ch[Rxy^1]; Link(b,y,Rxy); Link(y,x,Rxy^1); Link(x,r,Ryr); Update(y);Update(x); } void Splay(int x,int to){//将x节点旋至to int tfa=tr[to].prt; while(tr[x].prt!=tfa){//通过to的父亲判断x是否到达 int fa=tr[x].prt; if(tr[fa].prt!=tfa){ if(Rlt(x)==Rlt(fa)) Rotate(fa);//直的 else Rotate(x);//折的 }Rotate(x); } if(to==root) root=x;//改根 } int Create(int fa,int val){//建新节点 tr[++pn]=(Node){fa,{0,0},val,1,1}; return pn; } void Remove(int x){//清空节点数据 tr[x]=(Node){0,{0,0},0,0,0}; } void Init(){pn=0;Remove(0);root=0;} void Insert(int val){//插入值为val的节点 if(root==0){root=Create(0,val);return;}//无根 int x=root; while(1){ tr[x].sz++;//沿路更新size if(tr[x].val==val){tr[x].num++;break;}//已有节点，仅num++ bool R=val>tr[x].val; if(!tr[x].ch[R])//走到头 {x=tr[x].ch[R]=Create(x,val);break;}//创建，改儿子 x=tr[x].ch[R]; } Splay(x,root); } void Del(int val){ if(tr[root].ch[0]==0&&tr[root].ch[1]==0&&tr[root].num==1)//如果只剩根节点且只有一个值 {Remove(root);root=0;return;} int x=root; while(x){//找到删除节点 tr[x].sz--;//沿路更新size 注：本题保证不会删除原来没有的数，如果不保证需要对此处进行更改 if(tr[x].val==val) break; x=tr[x].ch[val>tr[x].val]; }if(!x) return;//找不到 if(tr[x].num>1){tr[x].num--;return;}//多于1个，仅num-- Splay(x,root);//旋上根 int lc=tr[x].ch[0],rc=tr[x].ch[1]; if(!lc)//无左子树 {tr[rc].prt=0,Remove(x),root=rc;return;}//右子树为根 int pre=lc; while(tr[pre].ch[1]) pre=tr[pre].ch[1];//找前驱 Splay(pre,lc);//前驱旋到左儿子 Link(rc,pre,1);//右儿子认前驱为父 tr[pre].prt=0,Remove(x),root=pre;//换根三连 Update(pre);//更新前驱（已经是根节点了），删除原点 } int GetRank(int val){//获得某数前有多少个数 int x=root,rk=0; while(x){ int lc=tr[x].ch[0],rc=tr[x].ch[1]; if(val==tr[x].val) {rk+=tr[lc].sz;break;} if(val<tr[x].val) x=lc; else rk+=tr[lc].sz+tr[x].num,x=rc; } if(x) Splay(x,root); return rk; } int Kth(int want){ int x=root,rk=0;want--; while(x){ int lc=tr[x].ch[0],rc=tr[x].ch[1]; int tmp=rk+tr[lc].sz; if(tmp<=want&&want<tmp+tr[x].num) break;//在这个区间内前头都有tmp个数，注意是给want限制了范围，而不是tmp if(want<tmp) x=lc; else rk=tmp+tr[x].num,x=rc; }if(!x) return 0; Splay(x,root); return tr[x].val; } int GetPre(int val){//获取第一个比val小的数 int x=root,ans=-INF; while(x){//尝试不停向val靠近并使x严格不大于等于val if(val<=tr[x].val) x=tr[x].ch[0]; else ans=max(ans,tr[x].val),x=tr[x].ch[1];//找到最大值 } return ans; } int GetNxt(int val){//获取第一个比val大的数 int x=root,ans=INF; while(x){ if(val<tr[x].val) ans=min(ans,tr[x].val),x=tr[x].ch[0]; else x=tr[x].ch[1]; } return ans; } }bst; int qn; int main(){; cin>>qn; bst.Init(); for(int i=1;i<=qn;i++){ int type;scanf("%d",&type); int x;scanf("%d",&x); switch(type){ case 1:{ bst.Insert(x); break;} case 2:{ bst.Del(x); break;} case 3:{ printf("%d\n",bst.GetRank(x)+1); break;} case 4:{ printf("%d\n",bst.Kth(x)); break;} case 5:{ printf("%d\n",bst.GetPre(x)); break;} case 6:{ printf("%d\n",bst.GetNxt(x)); break;} } } return 0; }
//2019/4/1 Update by sun123zxy #include<iostream> #include<cstring> #include<cmath> #include<cstdio> #include<ctime> #include<cstdlib> #include<algorithm> #include<queue> using namespace std; const int MXN=100005,INF=999999999; struct BST{ struct Node{ int fa,ch[2]; int val,sz,num; }tr[MXN]; int pn,root; void Update(int x){ int lc=tr[x].ch[0],rc=tr[x].ch[1]; tr[x].sz=tr[x].num+tr[lc].sz+tr[rc].sz; } bool Rlt(int x){return tr[tr[x].fa].ch[1]==x;} void Connect(int x,int fa,bool R){ if(x) tr[x].fa=fa; if(fa) tr[fa].ch[R]=x; } void Rotate(int x){ int y=tr[x].fa,r=tr[y].fa; bool Rxy=Rlt(x),Ryr=Rlt(y); int b=tr[x].ch[Rxy^1]; Connect(b,y,Rxy); Connect(y,x,Rxy^1); Connect(x,r,Ryr); Update(y);Update(x); } void Splay(int x,int to){ int gg=tr[to].fa; while(tr[x].fa!=gg){ int fa=tr[x].fa; if(tr[fa].fa!=gg){ if(Rlt(x)==Rlt(fa)) Rotate(fa); else Rotate(x); }Rotate(x); } if(to==root) root=x; } int Create(int fa,int val){ tr[++pn]=(Node){fa,{0,0},val,1,1}; return pn; } void Remove(int x){ tr[tr[x].ch[0]].fa=tr[tr[x].ch[1]].fa=0; tr[x]=(Node){0,{0,0},0,0,0}; } void Init(){pn=0;root=0;tr[0]=(Node){0,{0,0},0,0,0};} void Insert(int val){ if(!root){root=Create(0,val);return;} int x=root; while(x){ tr[x].sz++; if(val==tr[x].val){tr[x].num++;break;} bool R=(val>tr[x].val); if(!tr[x].ch[R]){ x=tr[x].ch[R]=Create(x,val); break;} x=tr[x].ch[R]; } Splay(x,root); } void Del(int val){ if(tr[root].ch[0]==0&&tr[root].ch[1]==0&&tr[root].num==1){ Remove(root);root=0; return;} int x=root; while(x){ tr[x].sz--;//注：本题保证不会删除原来没有的数，如果不保证需要对此处进行更改 if(val==tr[x].val) break; if(val<tr[x].val) x=tr[x].ch[0]; else x=tr[x].ch[1]; } if(!x) return; tr[x].num--; if(tr[x].num>0){return;} Splay(x,root); int lc=tr[x].ch[0],rc=tr[x].ch[1]; Remove(x); if(lc){ int nxt=lc; while(tr[nxt].ch[1]) nxt=tr[nxt].ch[1]; Splay(nxt,lc); Connect(rc,nxt,1);Update(nxt); root=nxt; }else root=rc; } int Rank(int val){ int x=root,rk=0; while(x){ int lc=tr[x].ch[0],rc=tr[x].ch[1]; if(val==tr[x].val){rk+=tr[lc].sz;break;} if(val<tr[x].val) x=lc; else rk+=tr[lc].sz+tr[x].num,x=rc; } if(!x) return -1; Splay(x,root); return ++rk; } int Kth(int K){ K--;int x=root,rk=0; while(x){ int lc=tr[x].ch[0],rc=tr[x].ch[1]; int tmp=rk+tr[lc].sz; if(tmp<=K&&K<tmp+tr[x].num) break; if(K<tmp) x=lc; else rk=tmp+tr[x].num,x=rc; } if(!x) return -INF; Splay(x,root); return tr[x].val; } int Pre(int val){//第一个比val小的数 int x=root,ans=-INF; while(x){ if(tr[x].val<val) ans=max(ans,tr[x].val); if(val<=tr[x].val) x=tr[x].ch[0]; else x=tr[x].ch[1]; } return ans; } int Nxt(int val){//第一个比val大的数 int x=root,ans=INF; while(x){ if(tr[x].val>val) ans=min(ans,tr[x].val); if(val<tr[x].val) x=tr[x].ch[0]; else x=tr[x].ch[1]; } return ans; } }splay; int qn; int main(){ cin>>qn;splay.Init(); for(int i=1;i<=qn;i++){ int type,x;scanf("%d%d",&type,&x); switch(type){ case 1:{ splay.Insert(x); break;} case 2:{ splay.Del(x); break;} case 3:{ printf("%d\n",splay.Rank(x)); break;} case 4:{ printf("%d\n",splay.Kth(x)); break;} case 5:{ printf("%d\n",splay.Pre(x)); break;} case 6:{ printf("%d\n",splay.Nxt(x)); break;} } } return 0; }
习题：
