cf920F SUM and REPLACE 树状数组+set 维护

题目:

Let D(x) be the number of positive divisors of a positive integer x. For example, D(2) = 2 (2 is divisible by 1 and 2), D(6) = 4 (6 is divisible by 1, 2, 3 and 6).

You are given an array a of n integers. You have to process two types of queries:

1. REPLACE l r — for every 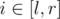 replace ai with D(ai);
2. SUM l r — calculate .

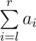Print the answer for each SUM query.

分析:

我们考虑到每个数可以进行操作的数量不会很多,且D(1)=1,D(2)=2.

我们只需要暴力修改就行了,然后用树状数组求和.

如何优雅的暴力?

也就是说如何快速找出区间[l,r]内满足ai>2的i值.考虑用set维护还可以操作的下标的点,每次用lb,ub去找.暴力修改.

另外筛1-1e6中每个数的因子个数的方法需要注意.

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAXN=3e5+7;
int N,M;
LL a[MAXN],val[MAXN];
int D[1000001];
inline int lowbit(int i){
    return i&-i;
}
LL sum(int x){
    LL res=0;
    while(x){
        res+=a[x];
        x-=lowbit(x);
    }
    return res;
}
void add(int i,int x){
    while(i<=N){
        a[i]+=x;
        i+=lowbit(i);
    }
}
int getD(long long x){
    return D[x];
}
int main(){
    for(int i=1;i<=1000000;++i){
        for(int j=i;j<=1000000;j+=i){
            D[j]++;
        }
    }
    scanf("%d%d",&N,&M);
    set<int>st;
    for(int i=1;i<=N;++i){
        scanf("%I64d",&val[i]);
        if(val[i]>2)st.insert(i);
        add(i,val[i]);
    }
    while(M--){
        int t,l,r;scanf("%d%d%d",&t,&l,&r);
        if(t==1){
            auto first=st.lower_bound(l);
            auto last=st.upper_bound(r);
            queue<int>q;
            while(first!=last){
                int i=*first;
                int x=getD(val[i]);
                add(i,x-val[i]);
                val[i]=x;
                if(x<=2)q.push(i);
                first++;
            }
            while(!q.empty()){
                int now=q.front();q.pop();
                st.erase(now);
            }
        }else{
            printf("%I64d\n",sum(r)-sum(l-1));
        }
    }
    return 0;
}