第四周作业:卷积神经网络(Part2)
一、理论学习
1、AlexNet的主要改进:在全连接层后增加丢弃法Dropout、使用ReLU减缓梯度消失、使用MaxPooling
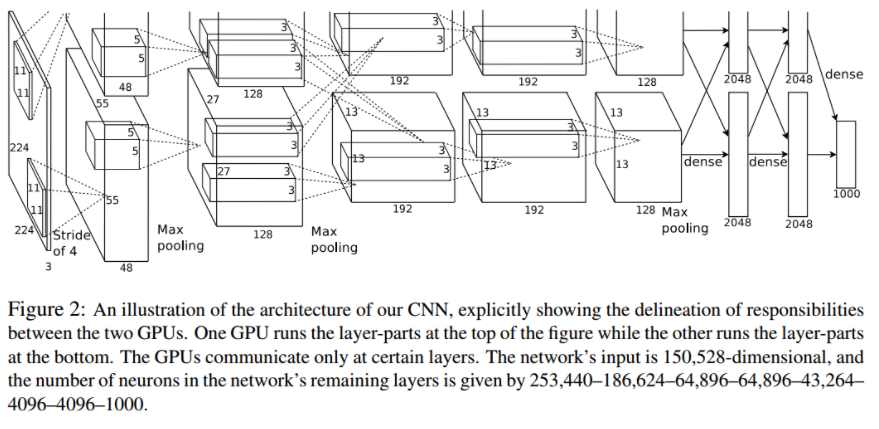
上下两层是两个GPU的结果,输入为227*227*3的图片(由224*224*3调整得来),第一层卷积的卷积核数量为96,卷积核大小为11*11*3,步长是4,padding=0,卷积后得到的图像大小feature map size为55*55*96,由于采用双CPU处理,所以数据分为两组,分别是55*55*48
池化运算里步长为2,卷积核大小为3*3,计算过程是(55-3)/2+1=27,池化后的图像尺寸为27*27*96
第二层卷积输入是27*27*96的像素层,步长为1,卷积核大小为5*5*256,padding=2,feature map 为27*27*256
池化运算里步长为2,卷积核大小为3*3,计算过程是(27-3)/2+1=13,feature map 为13*13*256
第三层卷积输入是13*13*128的像素层,步长为1,卷积核大小为3*3*384,padding=1,feature map 为13*13*384
第四层卷积输入是13*13*192的像素层,卷积核大小为3*3*384,padding=1,feature map 为13*13*384
第五层卷积输入是13*13*192的像素层,步长为1,卷积核大小为3*3*256,padding=1,feature map 为13*13*256
池化运算里步长为2,卷积核大小为3*3,计算过程为(13-3)/2+1=6,feature map 为6*6*256
第六层第七层是全连接层,神经元个数为4096,第八层全连接层神经元个数为1000,对应于ImageNet的1000类。
1 net = nn.Sequential( 2 nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(), 3 nn.MaxPool2d(kernel_size=3, stride=2), 4 nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(), 5 nn.MaxPool2d(kernel_size=3, stride=2), 6 nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(), 7 nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(), 8 nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(), 9 nn.MaxPool2d(kernel_size=3, stride=2), nn.Flatten(), 10 nn.Linear(6400, 4096), nn.ReLU(), nn.Dropout(p=0.5), 11 nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(p=0.5), 12 nn.Linear(4096, 10))
除此之外,AlexNet还应用了“局部响应归一化层”,形象来说对于13×13×256,由于不需要太多高激活神经元,LRN要选取一个位置,从这个位置穿过整个通道得到256个数字并进行归一化。但是LRN的效果并不理想。
2、VGG:更大更深的AlexNet,使用可重复使用的卷积块构建网络。网络非常庞大,需要训练的特征数量也很大。随着网络的加深,图像的高度和宽度都在以一定的规律不断缩小,每次池化后刚好缩小一半,而通道数量在不断增加,而且刚好也是在每组卷积操作后增加一倍。也就是说,图像缩小的比例和通道数增加的比例是有规律的。
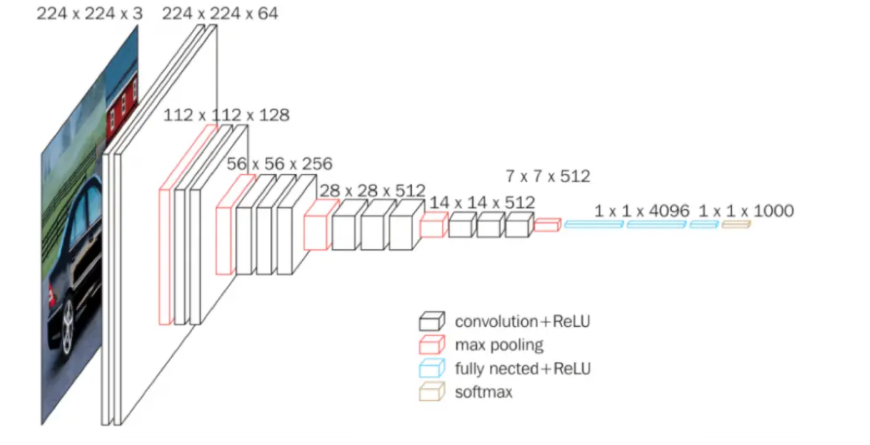
1 #vgg块 2 def vgg_block(num_convs, in_channels, out_channels): 3 layers = [] 4 for _ in range(num_convs): 5 layers.append( 6 nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)) 7 layers.append(nn.ReLU()) 8 in_channels = out_channels 9 layers.append(nn.MaxPool2d(kernel_size=2, stride=2)) 10 return nn.Sequential(*layers) 11 12 #vgg网络 13 conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512)) 14 15 def vgg(conv_arch): 16 conv_blks = [] 17 in_channels = 1 18 for (num_convs, out_channels) in conv_arch: 19 conv_blks.append(vgg_block(num_convs, in_channels, out_channels)) 20 in_channels = out_channels 21 22 return nn.Sequential(*conv_blks, nn.Flatten(), 23 nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), 24 nn.Dropout(0.5), nn.Linear(4096, 4096), nn.ReLU(), 25 nn.Dropout(0.5), nn.Linear(4096, 10))
3、NiN网络:由于全连接层参数多,会产生过拟合
无全连接层(NiN块里每个卷积后面两个全连接层)、交替使用NiN块和步长为2的最大池化层、最后使用全局平局池化得到输出。
1 def nin_block(in_channels, out_channels, kernel_size, strides, padding): 2 return nn.Sequential( 3 nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding), 4 nn.ReLU(), nn.Conv2d(out_channels, out_channels, kernel_size=1), 5 nn.ReLU(), nn.Conv2d(out_channels, out_channels, kernel_size=1), 6 nn.ReLU()) 7 8 net = nn.Sequential( 9 nin_block(1, 96, kernel_size=11, strides=4, padding=0), 10 nn.MaxPool2d(3, stride=2), 11 nin_block(96, 256, kernel_size=5, strides=1, padding=2), 12 nn.MaxPool2d(3, stride=2), 13 nin_block(256, 384, kernel_size=3, strides=1, padding=1), 14 nn.MaxPool2d(3, stride=2), nn.Dropout(0.5), 15 nin_block(384, 10, kernel_size=3, strides=1, padding=1), 16 nn.AdaptiveAvgPool2d((1, 1)), 17 nn.Flatten())
4、GoogLeNet
Inception块:4个路径从不同层面抽取信息,在输出通道维进行合并。输入被copy成4块,第一块进行1x1卷积,第二块先进行1x1卷积再进行3x3卷积(pad=1),第三块先进行1x1卷积再进行5x5卷积(pad=2),第四块先进行3x3的最大池化(pad=1)再进行1x1卷积。采用不同大小的卷积核意味着不同大小的感受野,最后拼接意味着不同尺度特征的融合。四块的总体特征是输出跟输入高宽不变,即等高等宽,但是通道数改变。GoogleNet使用了9个Inception块,最后通道数不断增大变为1024。

1 class Inception(nn.Module): 2 def __init__(self, in_channels, c1, c2, c3, c4, **kwargs): 3 super(Inception, self).__init__(**kwargs) 4 self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1) 5 self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1) 6 self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1) 7 self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1) 8 self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2) 9 self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1) 10 self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1) 11 12 def forward(self, x): 13 p1 = F.relu(self.p1_1(x)) 14 p2 = F.relu(self.p2_2(F.relu(self.p2_1(x)))) 15 p3 = F.relu(self.p3_2(F.relu(self.p3_1(x)))) 16 p4 = F.relu(self.p4_2(self.p4_1(x))) 17 return torch.cat((p1, p2, p3, p4), dim=1) 18 19 b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3), 20 nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2, 21 padding=1)) 22 23 b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1), nn.ReLU(), 24 nn.Conv2d(64, 192, kernel_size=3, padding=1), 25 nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) 26 27 b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32), 28 Inception(256, 128, (128, 192), (32, 96), 64), 29 nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) 30 31 b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64), 32 Inception(512, 160, (112, 224), (24, 64), 64), 33 Inception(512, 128, (128, 256), (24, 64), 64), 34 Inception(512, 112, (144, 288), (32, 64), 64), 35 Inception(528, 256, (160, 320), (32, 128), 128), 36 nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) 37 38 b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128), 39 Inception(832, 384, (192, 384), (48, 128), 128), 40 nn.AdaptiveAvgPool2d((1, 1)), nn.Flatten()) 41 42 net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))
5、批量归一化:底部数据梯度小,训练较慢,后面的层梯度较大,底层变化所有层要跟着变,导致收敛变慢。对全连接层,作用在特征维;对卷积层,作用在通道维。批量归一化可以放在输出激活函数前,也可以作用在输入上。通常使用nn.batchnorm函数完成批量归一化。
6、ResNet:串联一个残差块加入到右边得到f(x)=x+g(x),使得很深的网络容易训练。随着网络深度增加,梯度逐渐消失,因此引入了残差单元,将前面一层的输出直接连到后面的第二层,进而抑制了退化问题。ResNet的层数很深,借鉴了Highway Network思想,使得原来的拟合输出F(x)变成输出和输入的差F(x)-x,其中F(X)是某一层原始的的期望映射输出,x是输入。
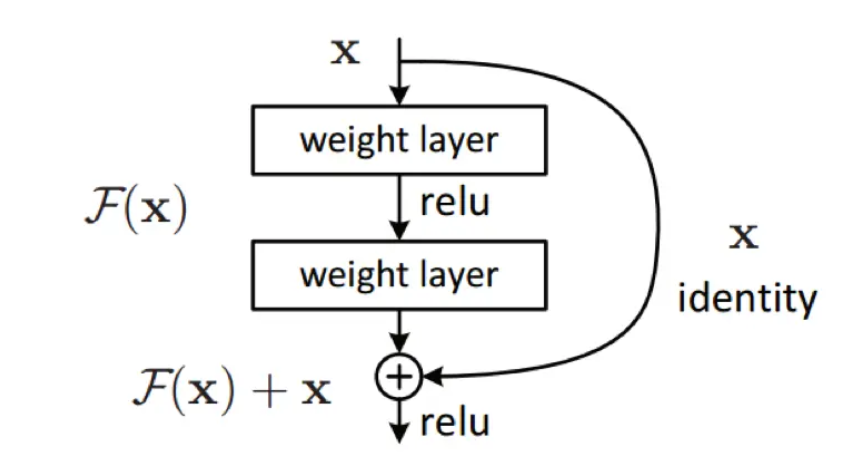
1 class Residual(nn.Module): 2 def __init__(self, input_channels, num_channels, use_1x1conv=False, 3 strides=1): 4 super().__init__() 5 self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3, 6 padding=1, stride=strides) 7 self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3, 8 padding=1) 9 if use_1x1conv: 10 self.conv3 = nn.Conv2d(input_channels, num_channels, 11 kernel_size=1, stride=strides) 12 else: 13 self.conv3 = None 14 self.bn1 = nn.BatchNorm2d(num_channels) 15 self.bn2 = nn.BatchNorm2d(num_channels) 16 self.relu = nn.ReLU(inplace=True) 17 18 def forward(self, X): 19 Y = F.relu(self.bn1(self.conv1(X))) 20 Y = self.bn2(self.conv2(Y)) 21 if self.conv3: 22 X = self.conv3(X) 23 Y += X 24 return F.relu(Y) 25 26 b1 = nn.Sequential(nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3), 27 nn.BatchNorm2d(64), nn.ReLU(), 28 nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) 29 30 def resnet_block(input_channels, num_channels, num_residuals, 31 first_block=False): 32 blk = [] 33 for i in range(num_residuals): 34 if i == 0 and not first_block: 35 blk.append( 36 Residual(input_channels, num_channels, use_1x1conv=True, 37 strides=2)) 38 else: 39 blk.append(Residual(num_channels, num_channels)) 40 return blk 41 42 b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True)) 43 b3 = nn.Sequential(*resnet_block(64, 128, 2)) 44 b4 = nn.Sequential(*resnet_block(128, 256, 2)) 45 b5 = nn.Sequential(*resnet_block(256, 512, 2)) 46 47 net = nn.Sequential(b1, b2, b3, b4, b5, nn.AdaptiveAvgPool2d((1, 1)), 48 nn.Flatten(), nn.Linear(512, 10))
二、使用ResNet完成猫狗大战
1、首先是使用李老师的resnet网络跑的猫狗大战,可以发现网络很不稳定,loss时大时小,得到的分类结果不如Alexnet。


2、使用models自带的resnet50跑猫狗大战,准确率还是不高,我都惊了~

主要是晓晨大佬看出了net.eval(),应用了net.eval()后准确率直线上升,非常nice。
1 net = models.resnet50(pretrained=True) 2 for param in net.parameters(): 3 param.requirse_grad = False 4 net.fc = nn.Linear(2048, 2, bias=True) # 二分类 5 6 print(net) 7 8 # 网络放到GPU上 9 net = net.to(device) 10 criterion = nn.CrossEntropyLoss() 11 optimizer = optim.Adam(net.fc.parameters(), lr=0.001) 12 for epoch in range(1): # 重复多轮训练 13 net.train() 14 for i, (inputs, labels) in enumerate(train_loader): 15 inputs = inputs.to(device) 16 labels = labels.to(device) 17 # 优化器梯度归零 18 optimizer.zero_grad() 19 # 正向传播 + 反向传播 + 优化 20 outputs = net(inputs) 21 loss = criterion(outputs, labels.long()) 22 loss.backward() 23 optimizer.step() 24 print('Epoch: %d loss: %.6f' %(epoch + 1, loss.item())) 25 print('Finished Training')

3、看到浩鹏对二分类的处理就很细致,2048直接到2估计会损失不少信息,再试着温柔的下降试试看~





