聚类：K-means与EM
写在前面
这是数据挖掘技术课程的课程笔记
复习的时候发现这些算法看似简单，但是蕴含了一些有趣的insight。在此加以记录。
K-means
K-means算法大家都很熟悉了：
首先随机分配K个centroid，
在每个iteration中：
把所有的数据点分配到最近的centroid。
计算每个centroid对应的cluster的均值，作为新的centroid。
或者如下图：
但是，K-means的算法流程为什么是这样的？或者说其背后的数学支撑是什么？
答案如下：
有以下几点值得注意：
1. 看起来K-means对数据的分布没有做任何前提假设，但是其优化的目标函数是Least Squares。因此它的本质是：对数据分布做高斯假设（一共有K类数据点。每一类数据点都服从：均值为对应的cluster centroid，协方差为单位阵的高斯分布），并求MLE。
2. K-means的参数有两个：μ和c。其中μ表示centoid的位置，c表示数据点所属的centroid。
3. K-means的优化过程是coordinate decent。先优化c，再优化μ。
4. 这种优化方式容易陷入局部最优。因此需要跑多次K-means算法，并取J最小的那一次作为最终结果。
P.S. 在EM中，我们同样会使用coordinate decent这种优化方式。
EM
EM也是非常经典的聚类算法。
它与K-means算法对数据分布的假设类似：以各个centroid为均值的高斯分布。但是它比K-means更宽松：
它不再假设协方差为单位阵，而是假设为对角阵。
也就是说，每个cluster都是一个 "axis-aligned ellipse"。
引入这个relaxation之后，求MLE变得复杂。
为了方便建模，引入隐变量z，满足多项分布（multinomial distribution）。它描述x属于不同cluster的概率。
在引入z后，我们可以写出MLE的形式（见下图）
想要使此式最大，难点在于黄框中的求和号。它导致了logΣ这种形式的出现，不利于求导。
反之，若我们已知了z（已知了x应该属于那个cluster），那么可以去掉这个求和号，并轻易地求出MLE最大化对应的参数，如下图：
说到这里，我们先放出EM算法的流程，再阐述它的具体推导和数学含义。
可以发现，这里M step中求出的三个参数与上一张图中的十分类似。直觉上理解，M step看作对参数的soft guess（按概率计数，而不是按个数计数）。
当然，这种理解没有数学依据。要想知道算法流程为什么是这样的，光靠直觉是不够的。
在了解EM的推导之前，要知道琴生不等式。
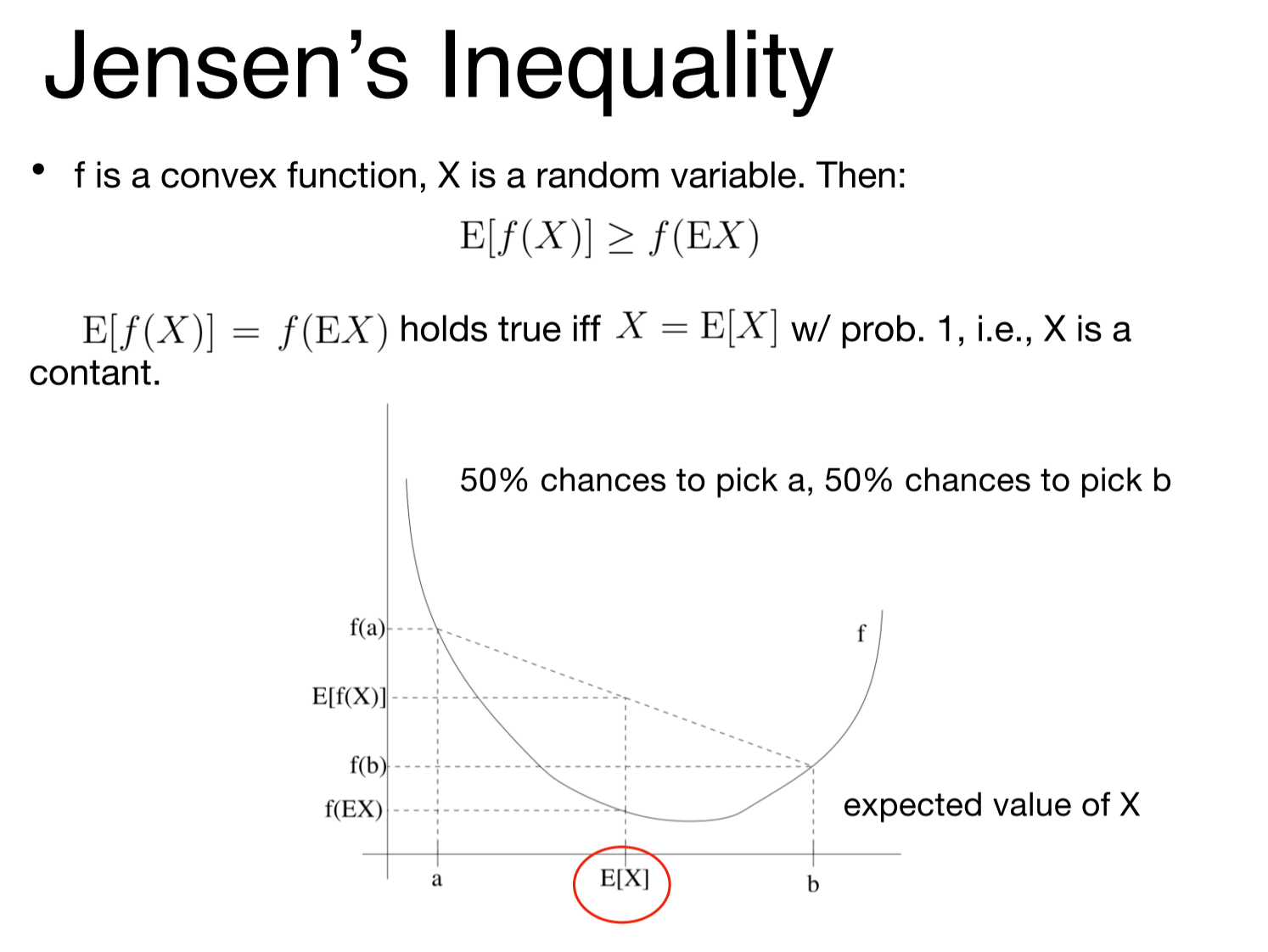
关于琴生不等式，讲一句题外话，但是很重要：
不能直接利用琴生不等式做最优化！
假设函数ƒ2与ƒ1满足下图关系：
类似琴声不等式，这里有ƒ2≤ƒ1恒成立。但是当ƒ2=ƒ1时，ƒ2并不能取到极大值！
也就是说，要想对ƒ2最优化，不能利用琴生不等式！我们应该老老实实求导，求得极大值。
题外话讲完，继续推导：
为了避免logΣ的出现，引入概率Q，利用琴生不等式（log是个凹函数），将Σ移到log外面。
Q的选取：需要让琴生不等式取等。发现Q应该取后验概率P(z|x)
关于后验概率的求法，可以按照贝叶斯公式来做（并将贝叶斯公式的分母看作归一化）。即：对于K种可能的z的取值，求P(z)*P(x|z)，再归一化。
到这里可以总结一下：
我一开始看这里时是有疑惑的：不是通过让Q等于后验概率的方式，让琴生不等式取等了吗？这里为什么还说lower bound？
答案是这样的：
如果我们去掉E-step，不先求出Q，而仍然把Q看作关于theta的函数，那么琴生不等式在优化过程中将保持等号成立，并不是优化lower bound。
但是这样一来，我们先前的变形将毫无意义（目标函数的本质没有变，仍然是个logΣ，难以求导）。
做变形的目的，是为了方便地求出theta的解析解。因此我们将Q固定（E-step），仅让theta出现在log项的分子中。这样可以方便地求导优化。
因此，注意在下面这张图中黄框框起来的部分是Q(t),而不是Q(t+1)。由琴生不等式，Q(t)与θ(t+1)的这个搭配，是小于等于MLE的。
可以证明，通过这种方式优化，可以使MLE非递减。
到这里，EM的原理就说清楚了。
可以把EM看作coordinate ascent：先调整Q，再调整θ。
但是与标准的coordinate ascent的区别在于：此处调整Q并不是让琴生不等式变形后的右侧取到它的极大值，而是取到与左侧相等！（见上面的题外话）
（对J求导，可以得到上面soft guess的参数更新公式。此处略去。）
EM中这种 “引入Q，使用琴生不等式避免logΣ” 的套路在复杂的机器学习模型里面也很常见。我记得在强化学习policy iteration中用到了这个技巧，但不是很确定。
深入的理解它对日后学习复杂模型将会很有帮助。
结语
虽然Kmeans与EM都是非常非常基础的机器学习聚类算法，但是俗话说得好：万变不离其宗。
它们中的一些insight和推导套路，仍然是值得学习的。
