【数据结构与算法】—— 归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序是一种稳定的排序方法。
归并介绍
前面有介绍,这里依然不做介绍
归并思想
核心思想:不断的将大的数组分成两个小数组,直到不能拆分为止,即形成了单个值。此时使用合并的排序思想对已经有序的数组进行合并,合并为一个大的数据,不断重复此过程,直到最终所有数据合并到一个数组为止。
归并分析
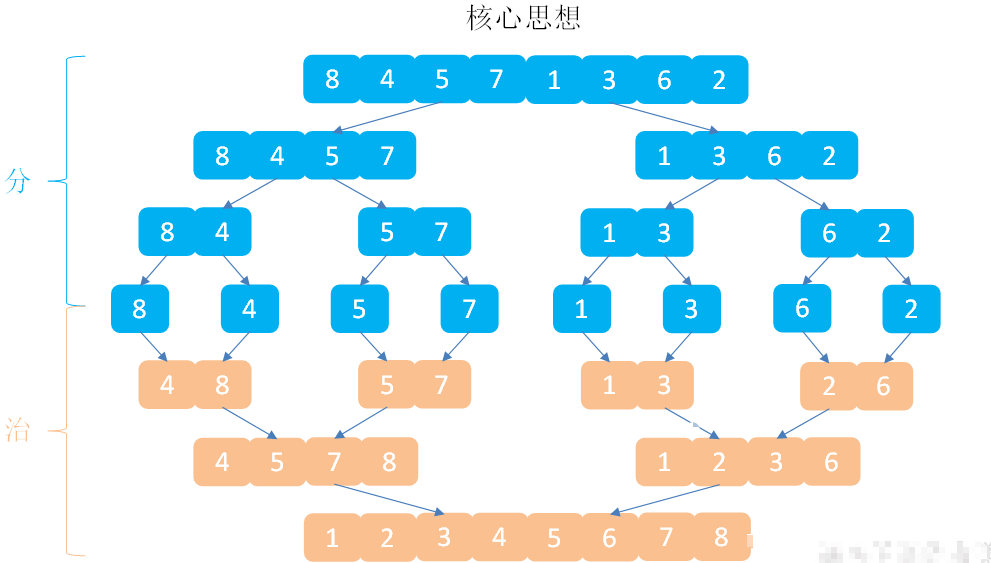
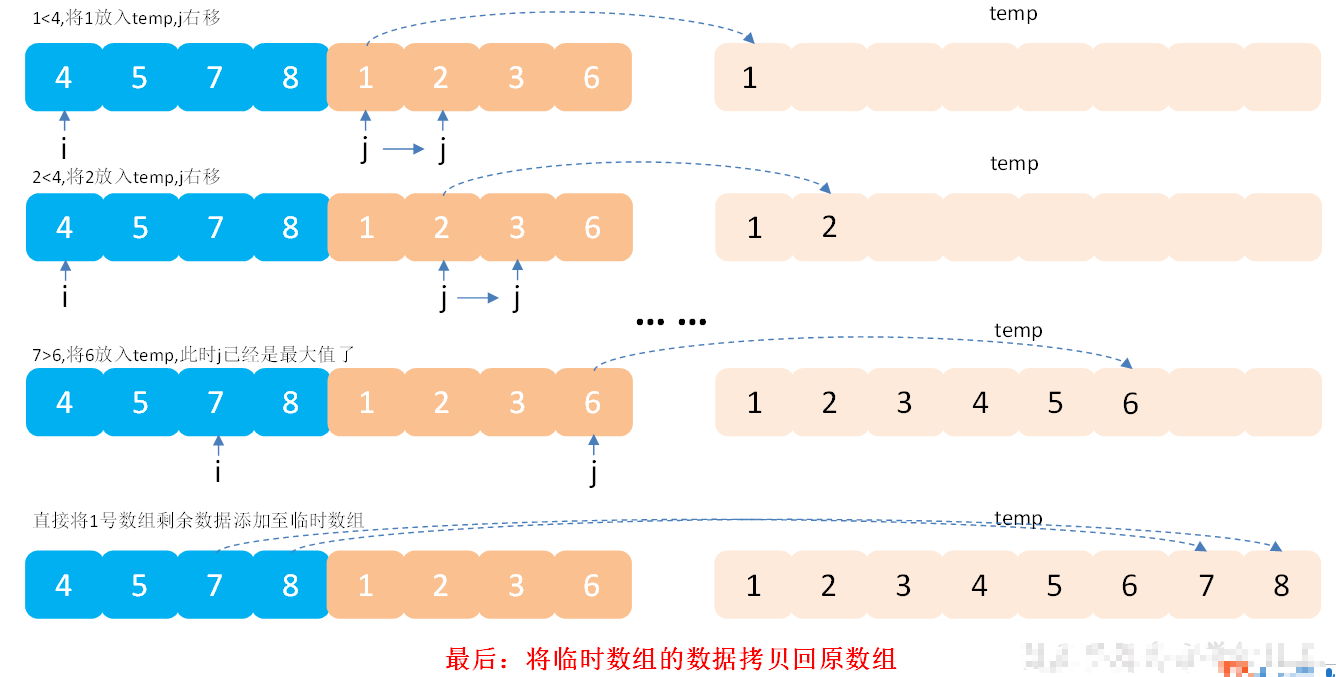
我在网上看到一大神写的关于 归并排序的图解,很清楚明了。可以借鉴一下: 【图解】归并排序
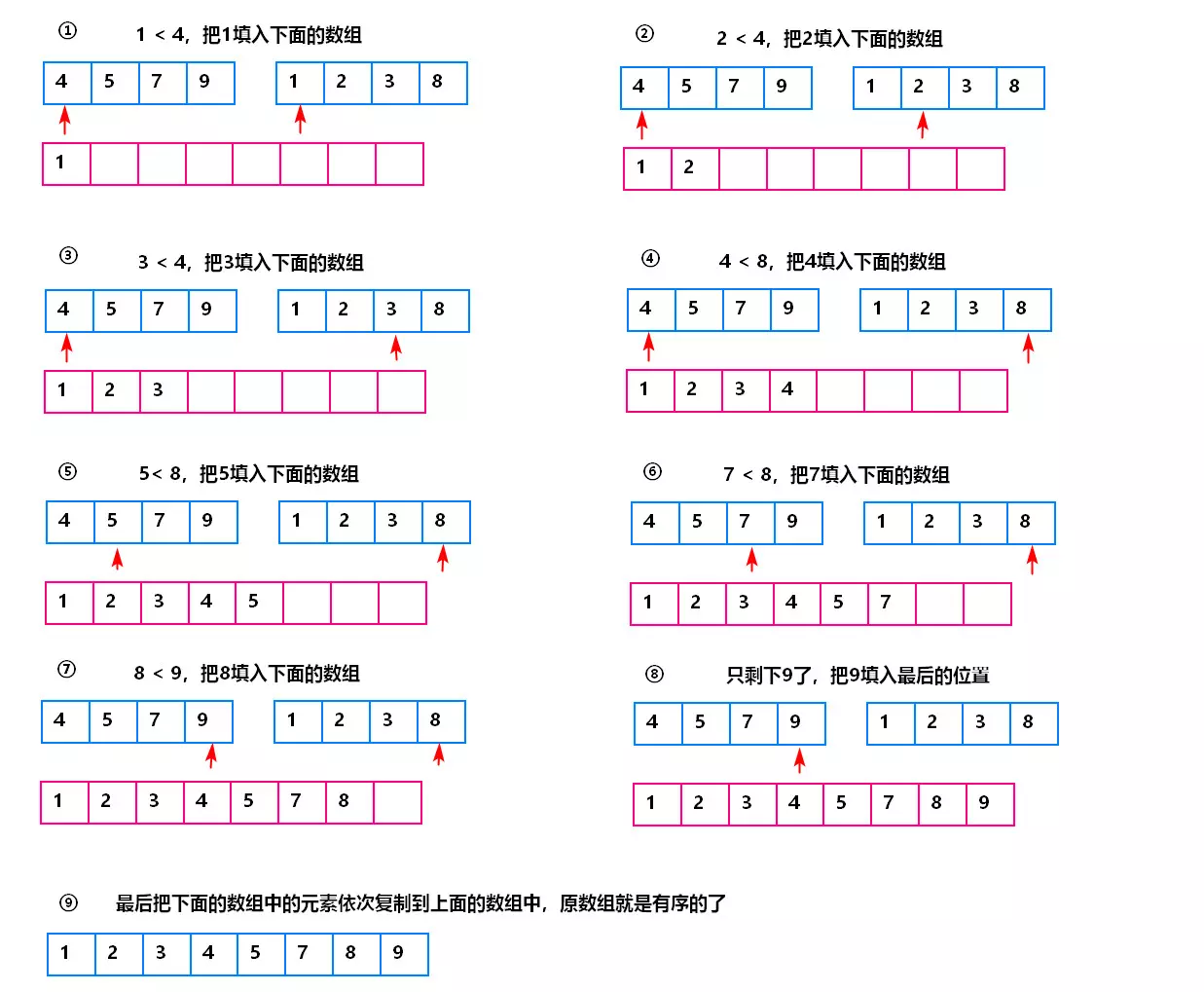
图解归并-动态
代码实现
Java程序是网上得到哪位大神提供的。
public static void main(String[] args) {
int[] data = {8, 4, 5, 7, 1, 3, 6, 2};
mergeSort(data);
System.out.println(Arrays.toString(data));
}
public static void mergeSort(int[] arr) {
sort(arr, 0, arr.length - 1);
}
public static void sort(int[] arr, int L, int R) {
if (L == R) {
return;
}
int mid = L + ((R - L) >> 1);
sort(arr, L, mid);
sort(arr, mid + 1, R);
merge(arr, L, mid, R);
}
public static void merge(int[] arr, int L, int mid, int R) {
int[] temp = new int[R - L + 1];
int i = 0;
int p1 = L;
int p2 = mid + 1;
// 比较左右两部分的元素,哪个小,把那个元素填入temp中
while (p1 <= mid && p2 <= R) {
temp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
// 上面的循环退出后,把剩余的元素依次填入到temp中
// 以下两个while只有一个会执行
while (p1 <= mid) {
temp[i++] = arr[p1++];
}
while (p2 <= R) {
temp[i++] = arr[p2++];
}
// 把最终的排序的结果复制给原数组
for (i = 0; i < temp.length; i++) {
arr[L + i] = temp[i];
}
}
def main(args: Array[String]): Unit = {
var left: List[Int] = List(
4, 5, 7, 8
)
var right: List[Int] = List(1, 2, 3, 6)
val ints: List[Int] = merge(left, right)
println(ints)
}
def merge(left: List[Int], right: List[Int]): List[Int] = (left, right) match {
case (Nil, _) => right
case (_, Nil) => left
case (x :: xTail, y :: yTail) =>
if (x <= y) x :: merge(xTail, right)
else y :: merge(left, yTail)
}
在归并之前,首先先要对两个数组做排序,要保证他们两个有序,然后在进行归并。之前的有序的过程可以使用快速排序算法。
在归并中,一般会使用 快排 + 归并 来完成一个数组的排序。
时间复杂度:O(nlogn)
空间复杂度:O(N),归并排序需要一个与原数组相同长度的数组做辅助来排序


 浙公网安备 33010602011771号
浙公网安备 33010602011771号