主成分分析 (Principal Component Analysis，PCA)

　　主成分分析 (Principal Component Analysis，PCA) 是一种常用的无监督学习方法，这一方法利用正交变换把由线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据，线性无关的变量称为主成分。

1 PCA 基本想法

　　主成分分析中，首先对给定数据进行中心化，使得数据每一变量的平均值为 0。之后对数据进行正交变换，原来由线性相关变量表示的数据，通过正交变换成若干个线性无关的新变量表示的数据。新变量是可能的正交变换中变量的方差和 (信息保存) 最大的，方差表示在新变量上信息的大小。

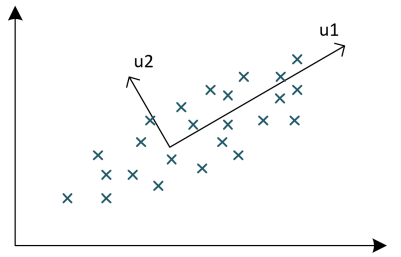
　　例如，图中的数据在 u₁ 方向上的投影明显比 u₂ 好，因为数据投影后的方差更大，保存的信息更多。我们可以再找一个与 u₁ 线性无关且投影后方差最大的向量，即 u₂ 。因为这里只是二维的，所以最多两个线性无关的新变量，这两个新变量依次称为第一主成分(u₁)、第二主成分(u₂)。

　　这就是 PCA 的基本思想。通过 PCA，可以利用主成分近似地表示原始数据，这可理解为发现数据的“基本结构”；也可以把数据由少量主成分表示，这可理解为对数据降维。

　　对于 PCA 降维的更直观的解释：将数据投影到新坐标系的坐标轴上，新坐标系的第一坐标轴、第二坐标轴等分别表示第一主成分、第二主成分等，数据在每一轴上的坐标值的平方表示相应变量的方差 (因为已经中心化过了)，并且，这个坐标系是在所有可能的新的坐标系中，坐标轴上的方差和最大的。

2 PCA 的推导

　　一般来说，PCA 有两种解释：第一种解释是样本点到这个直线的距离足够近，即基于最小投影距离；第二种解释是样本点在这个直线上的投影能尽可能的分开，即基于最大投影方差。两种解释的推导是等价的，下面主要介绍基于最大投影方差的推导。

　　假设 n 个 d 维数据 X = ( x₁，x₂ ，...，x_n )，都已进行了中心化。经过投影变换后得到的新坐标系为 { w₁，w₂，...，w_d }，其中 w 是标准正交基，即 ‖w‖₂ = 1，w_i^Tw_j = 0。如果我们将数据从 d 维降到 k 维 ( k < d )，那么我们仅保留前 k 个主成分 { w₁，w₂，...，w_k }。

　　对于任意一个样本 x_i，在新的坐标系中的投影为 W^Tx_i，在新坐标系中的投影方差为 x_i^TWW^Tx_i，要使所有的样本的投影方差和最大，也就是最大化 W^TXX^TW 的迹的和，即：

　　利用拉格朗日函数可以得到：

　　对 W 求导有 XX^TW + λW = 0，整理下即为：

　　可以看出， -λ 为 XX^T 的最大的 k 个特征值组成的矩阵，特征值在主对角线上，其余位置为 0，而 W 为 XX^T 的 k 个特征值对应的特征向量组成的矩阵。最后，对于原始数据集，我们只需要用 W^Tx_i 就可以把原始数据集降到 k 维数据集。

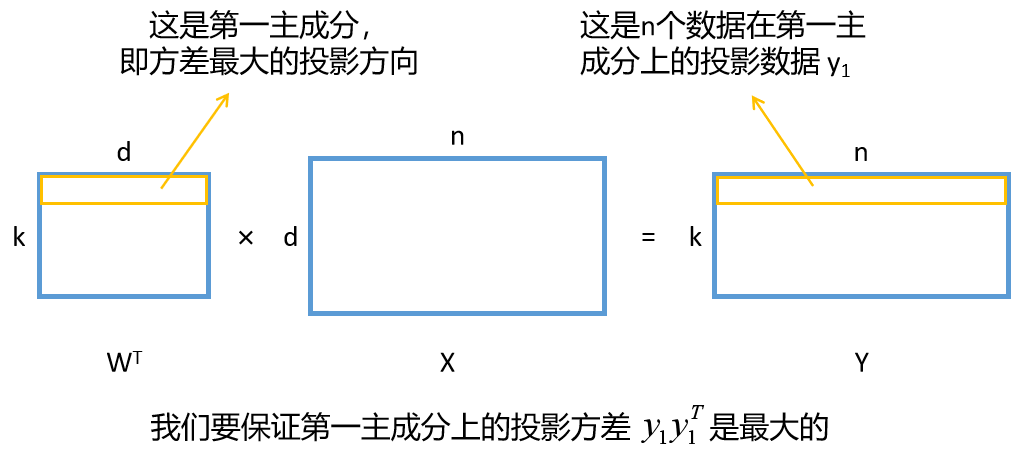
　　一般，y_i 是与 y₁，y₂，...，y_i-1 都不相关的 X 的所有线性变换中方差最大的，即第 i 主成分。

　　X 的第 i 主成分的方差是：

　　即协方差矩阵 XX^T 的第 k 个特征值。

3 PCA 算法流程

　　从上面两节我们可以看出，求样本 x_i 的 k 维的主成分其实就是求样本集的协方差矩阵 XX^T 的前 k 个特征值对应特征向量矩阵 W，然后对于每个样本 x_i 做如下变换 z_i =  W^Tx_i ，即达到降维 PCA 的目的。

　　具体的算法流程：

　　输入： n 个 d 维数据集 X = ( x₁，x₂ ，...，x_n )，要降到的维数 k 。

　　输出：降维后的样本集 Z

　　(1) 对所有样本进行中心化；

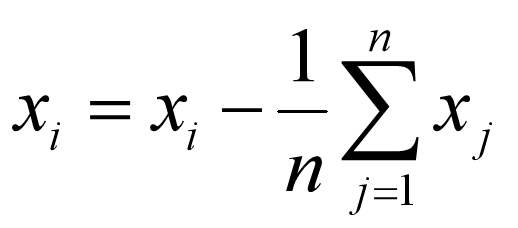
　　(2) 计算样本的协方差矩阵 XX^T ；

　　(3) 对矩阵 XX^T 进行特征值分解；

　　(4) 取出最大的 k 个特征值对应的特征向量 { w₁，w₂，...，w_k }，将所有的特征向量标准化后，组成特征向量矩阵 W ；

　　(5) 对样本集中的每一个样本 x_i ，转化为新的样本  z_i =  W^Tx_i ；

　　(6) 得到输出样本集 Z。

　　有时候，我们不指定降维后的 k 的值，而是换种方式，指定一个降维到的主成分比重阈值 t 。这个阈值 t 在 ( 0，1 ] 之间。假如我们的 n 个特征值为 λ₁ ≥ λ₂ ≥ ... ≥ λ_n，则 k 可以通过下式得到：

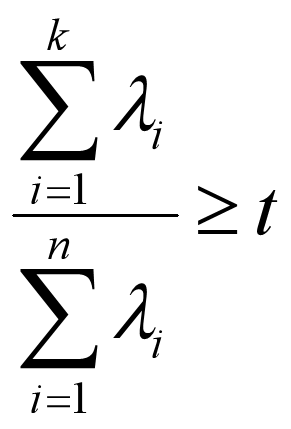
　　在一些实际应用中，第 (3) 步的特征值分解往往会用奇异值分解 (SVD) 代替，一些 SVD 的算法可以在不计算 XX^T 的情况下，直接计算 XX^T 的特征向量，降低了计算复杂度。

4 总结

　　这里对 PCA 算法做一个总结。作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服 PCA 的一些缺点，出现了很多 PCA 的变种，比如为解决非线性降维的 KPCA，还有解决内存限制的增量 PCA 方法 Incremental PCA，以及解决稀疏数据降维的 PCA 方法 Sparse PCA 等。

　　PCA 算法的主要优点有：

　　1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。　

　　2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

　　3）计算方法简单，主要运算是特征值分解，易于实现。

　　PCA 算法的主要缺点有：

　　1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

　　2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

 

 

主要参考：PCA 原理总结、李航《统计学习方法》