如何理解矩阵乘法
如果学过《线性代数》，那么你应该对矩阵乘法计算规则有所了解，但为什么要这样计算呢？矩阵乘法有什么用呢？下面以理解矩阵乘法为目的来介绍。
1 高斯消元法
首先，矩阵的本质其实就是线性方程组，而解线性方程组的通用方法就是高斯消元法。
1.1 高斯消元法的思路
给出一个简单的例子，需要求解以下线性方程组：
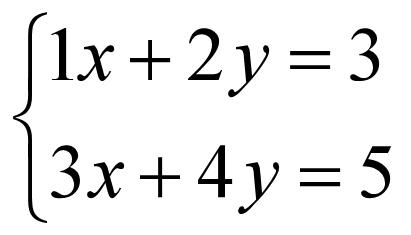
从几何上来讲，线性方程都是直线，求解方程组就是找到两个直线的交点：
最终的目标就是把方程组化成这个样子：
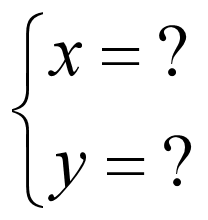
要达到这个目标，高斯消元法的思路是，先用第一行方程式消除后面方程式的某一未知数：
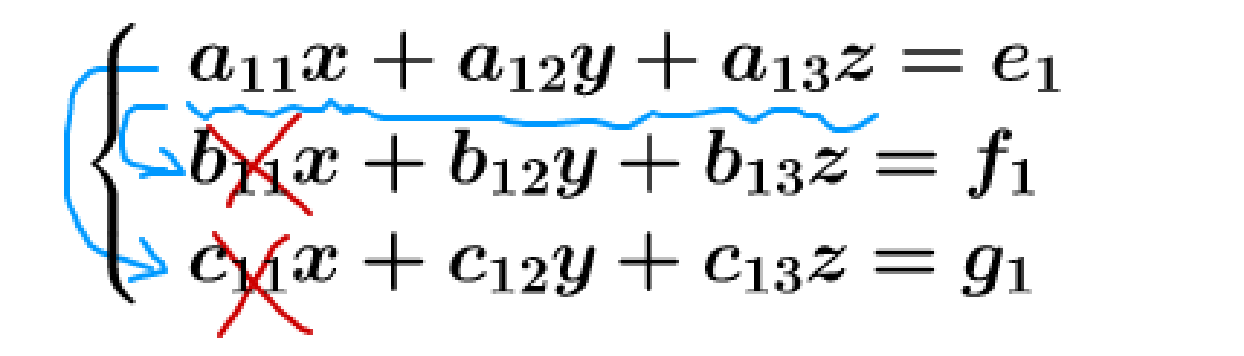
同样，用第二行把这些消了：
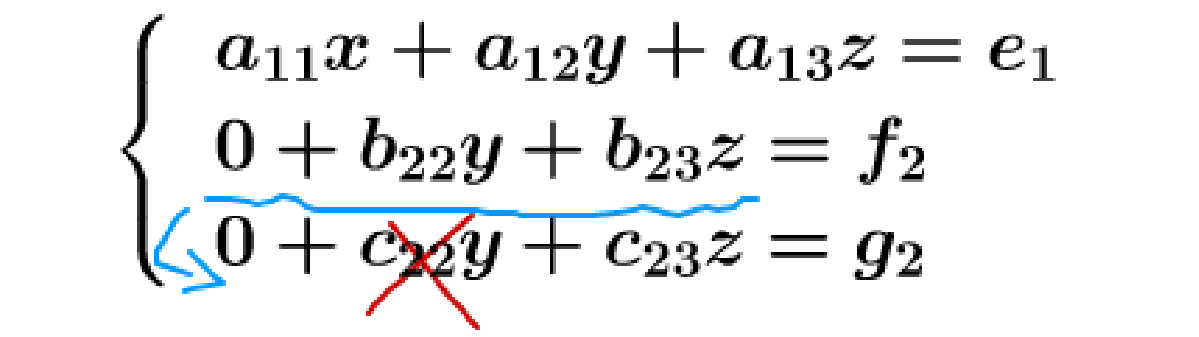
反过来，用第三行把这些给消了：
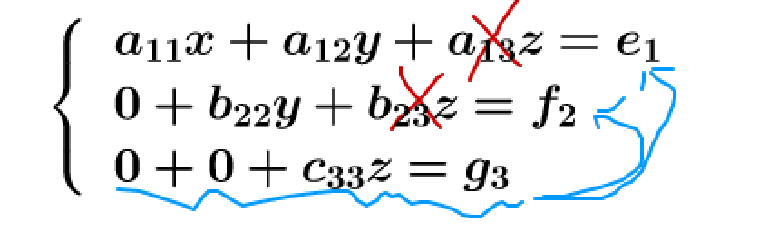
反过来，用第二行把这些给消了：
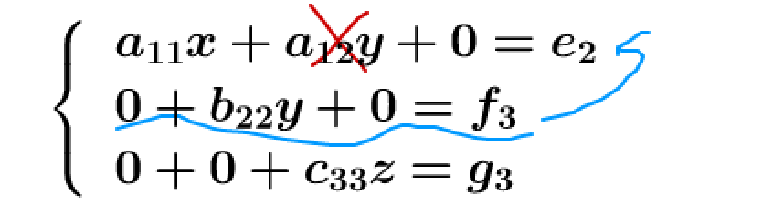
最后，达到目标：
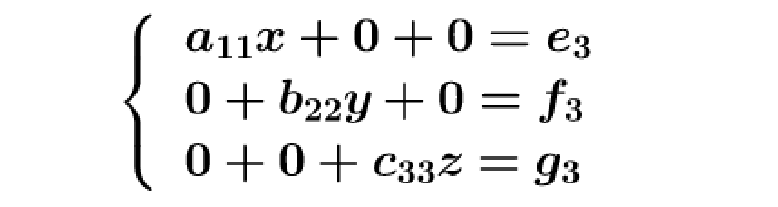
接下来让我们用该思路求解该方程组：
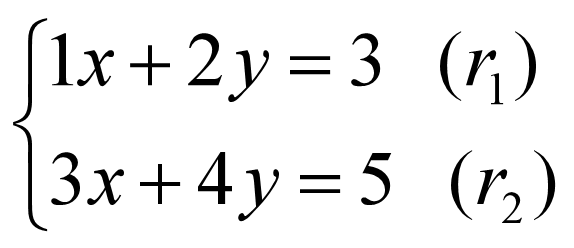
完整的解题过程如下：
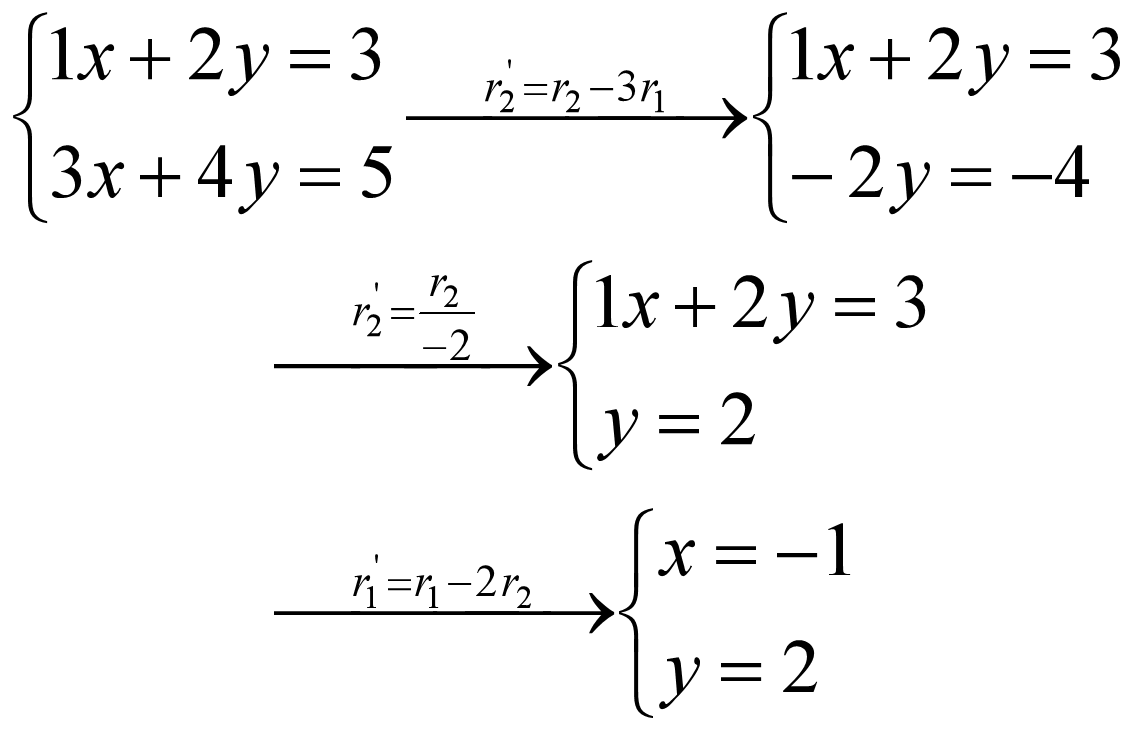
至此，解出答案：
1.2 凯莱的高斯消元法
英国数学家阿瑟·凯莱（1821－1895）对于看似简单的高斯消元法进行了研究，得出了惊人的结果。他当时研究矩阵的动机出于对线性方程组计算的简化。
对于一个这样的方程组：
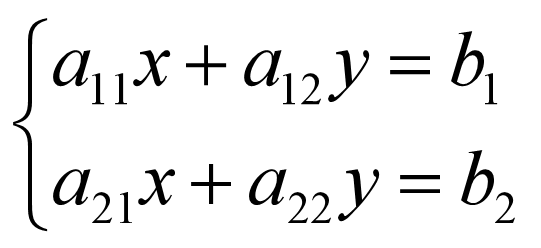
在固定未知数的顺序（x 出现在第一个位置，y 出现在第二个位置，常数在等号右边）后，且保证每个未知数都出现(不出现时，系数为0)，方程组就只需要系数来表示了。该方程组可以简写为如下数块：
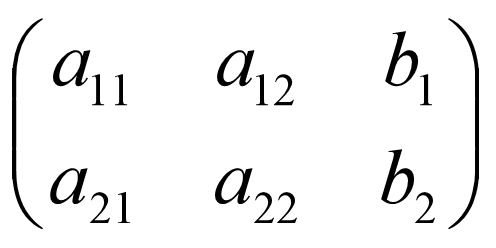
之前说过，高斯消元法的目标是：
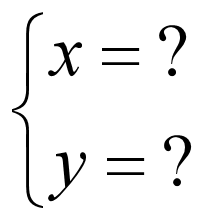
因此我们的目标就是要把数块变成下面这个样子：
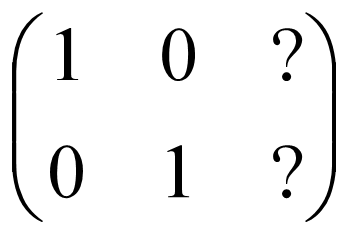
对应之前的高斯消元法：
得到结果：
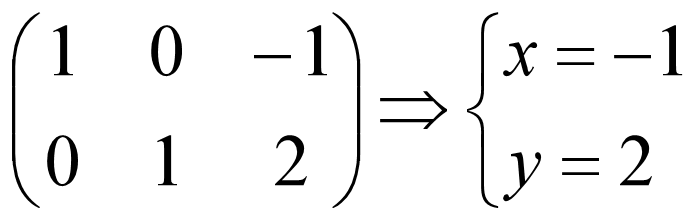
正如你看到的，解起来并不复杂，但是要将过程描述清楚却很繁琐，这很不数学。能不能更优雅的展现这个过程呢？
1.3 数块乘法
数学家发明了一种数块的乘法，简洁地进行高斯消元法。
1) 单行乘法
对于：
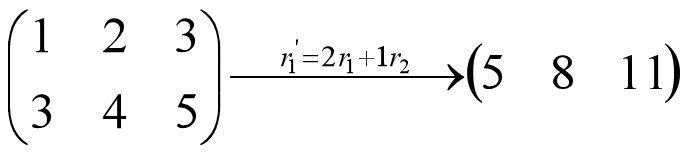
用数块乘法表示为：
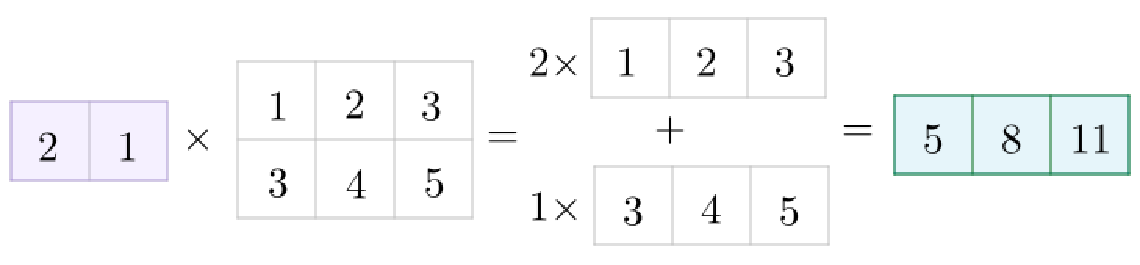
2) 多行乘法
对于：
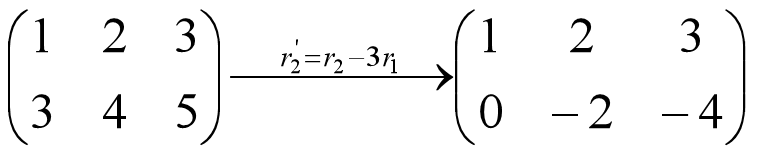
它表达了两个过程：
- 第一行不变：r1' = r1
- 第二行改变：r2' = r2 - 3r1
用数块乘法表示为：
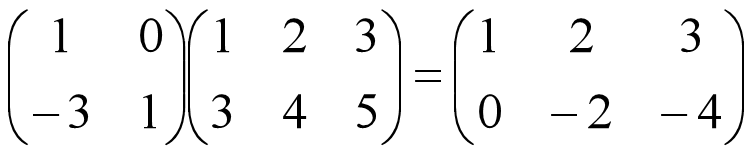
即按照单行乘法的规则，只是第一行运算的结果放在第一行，第二行运算的结果放在第二行：
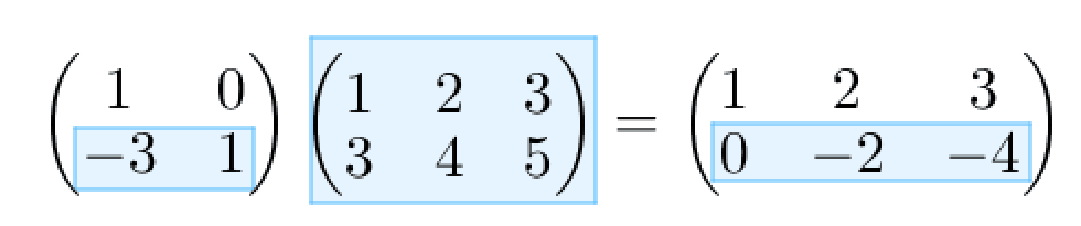
有了这个运算规则后，整个高斯消元法就可以表示如下:
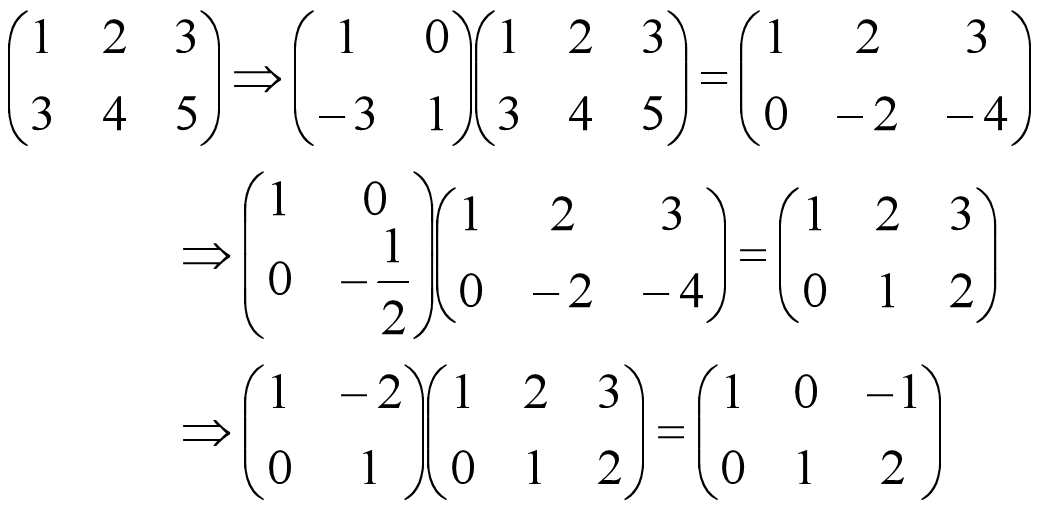
1.4 矩阵的定义
阿瑟·凯莱在1858年的《矩阵理论纪要》的论文中，给这个数块以合法的数学地位，取了一个名字：矩阵。
由 m × n 个数 aij ( i = 1,2,...,m ; j = 1,2,...,n ) 排成的 m 行 n 列的数表称为 m 行 n 列矩阵，简称 m × n 矩阵。为表示它是一个整体，总是加一个括弧，并用大写黑体字母表示它，记做：
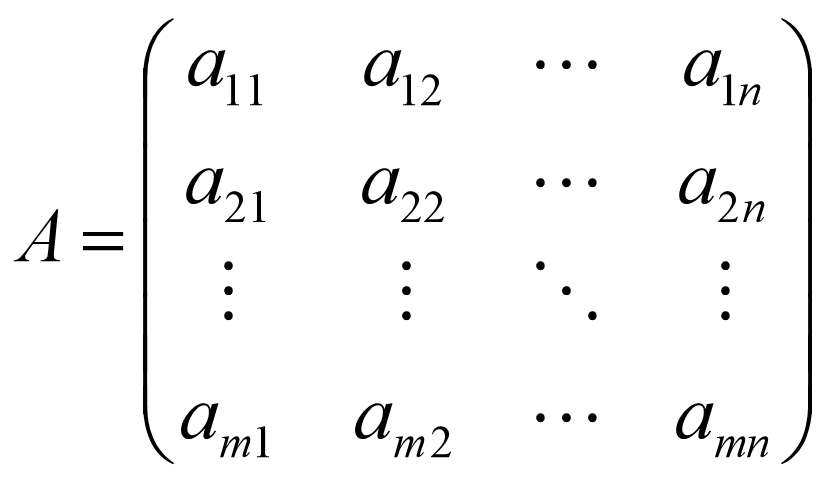
这 m × n 个数称为矩阵 A 的元素。
2 矩阵是一个映射函数
更好的理解方式是把矩阵看做函数，或者说是一种映射。例如：
矩阵 A 将一个 n 维向量 x 映射为 m 维的向量 y。
为了更好的理解这种映射，下面给出具体的例子。研究线性映射，最重要的是搞清楚当前处在哪个基下。我们先来看看：
x、y 的基默认为各自向量空间下的自然基，其自然基为（即 R2 下的自然基）：
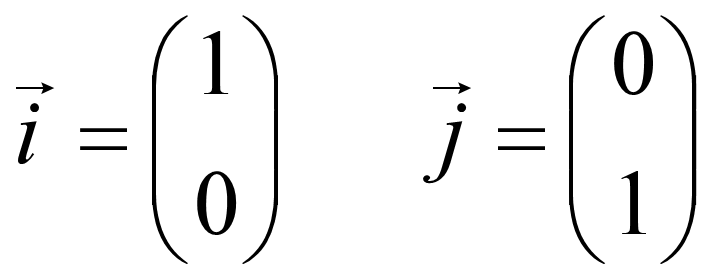
所以：
若：
其中 c1，c2 为 A 的列向量。
根据矩阵乘法规则有：
则 Ax 相当于在 A 空间中，以 c1，c2 为基，坐标为 ( x1，x2 ) 的向量。
假设：
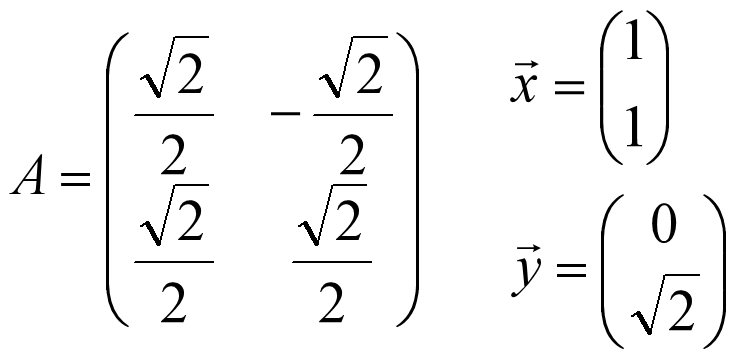
则有：
空间 V 通过 A 映射到 W。整体来说，就是基改变，导致向量的坐标发生变化。
可以把 A 比喻成穿越时空的传送门，只是这是一个比较死板的传送门，它的传送规则是，根据你进入传送门的时空坐标，把你送到另外一个时空对应的位置。
我的理解是，x 本来在以矩阵 A 的列向量为基底的空间中，现在 A 是用空间 W 中的自然基底表示的，x 通过左乘 A 转换到在当前空间 W 所在坐标 y。
下一节：特征值与特征向量
主要参考：从高斯消元法到矩阵乘法、如何理解矩阵乘法？
