特征值和特征向量

1 基本定义

　　设 A 为 n 阶方阵，若存在数 λ 和非零向量 x，使得：

　　则称 λ 是 A 的一个特征值，x 为 A 的对应于特征值 λ 的特征向量。

　　先有一个直观的印象：可以把矩阵看做是运动，特征值就是运动的速度，特征向量就是运动的方向。

　　注意，由于矩阵是数学概念，非常抽象，所以上面所谓的运动、运动的速度、运动的方向都是广义的，在现实不同的应用中有不同的指代。

2 几何意义

　　因为线性变换总是在各种基之间变来变去，所以下面都会把作图所用的基和原点给画出来。

　　在\vec{i_{}},\vec{j_{}}下面有个\vec{v_{}}：

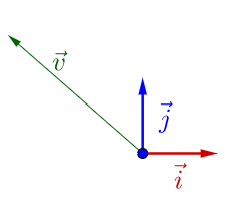
　　随便左乘一个矩阵 A，图像看上去没有什么特殊的：

　　调整下\vec{v_{}}的方向，图像看上去有点特殊了：

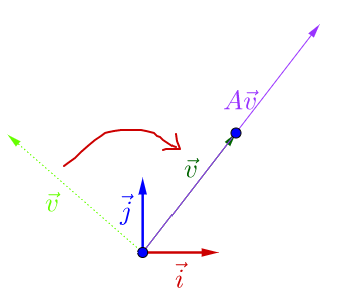
　　可以观察到，调整后的 \vec{v_{}} 和 A\vec{v_{}} 在同一根直线上，只是 A\vec{v_{}} 的长度相对 \vec{v_{}} 的长度变长了。

　　此时，我们就称 \vec{v_{}} 是 A 的特征向量，而 A\vec{v_{}} 的长度是\vec{v_{}}的长度的 \lambda 倍，\lambda 就是特征值。

　　从而，特征值与特征向量的定义式就是这样的：

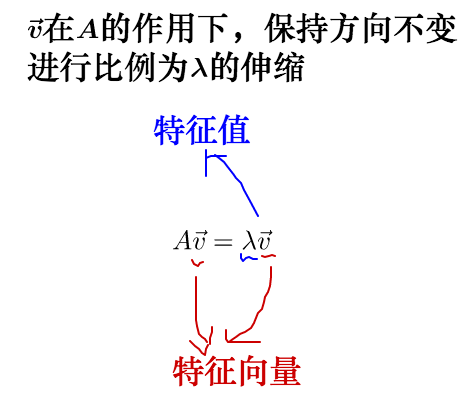
　　其实之前的 A 不止一个特征向量，还有一个特征向量：

　　容易从A\vec{v_{}}相对于\vec{v_{}}是变长了还是缩短看出，这两个特征向量对应的特征 \lambda 值，一个大于1，一个小于1。

　　从特征向量和特征值的定义式还可以看出，特征向量所在直线上的向量都是特征向量：

　　可以尝试改变 \vec{v_{}} 的位置，以及矩阵 A 的值 (特征空间会随着矩阵改变而改变) 。有些值构成的矩阵没有画出特征空间，可能是因为它的特征值、特征向量是复数，也可能是不存在。

　　运动需要附加到具体的事物上才能观察，要观察矩阵所代表的运动，需要把它附加到向量上，可以把二维向量可以看作平面上的一个点：

　　似乎还看不出什么。但是如果反复运用矩阵乘法的话：

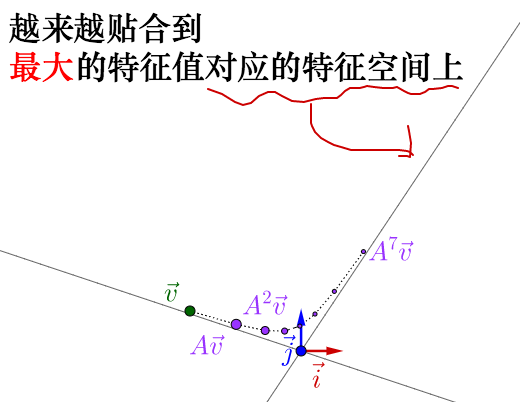
　　反复运用矩阵乘法，矩阵所代表的运动的最明显的特征，即速度最大的方向，就由最大特征值对应的特征向量展现了出来。顺便说下，对于复数的特征值、特征向量可以观察到反复运用矩阵乘法的结果是围绕着原点在旋转，这里就不展开来说了。

3 相似矩阵

　　相似矩阵的定义是：设 A，B 都是 n 阶矩阵，若有可逆矩阵 P，使 P-1AP = B ，则称 B 是 A 的相似矩阵，或说 A 和 B 相似。

　　这部分内容会涉及到矩阵乘法的知识，可以参考：如何理解矩阵乘法。可以了解到，矩阵是一种线性变换函数，这种线性变换是通过指定基下的矩阵 A 来表示的。

　　相似矩阵就是，同一个线性变换，不同基下的矩阵。

　　先上一张图，说明不同基下的矩阵的变换思路：

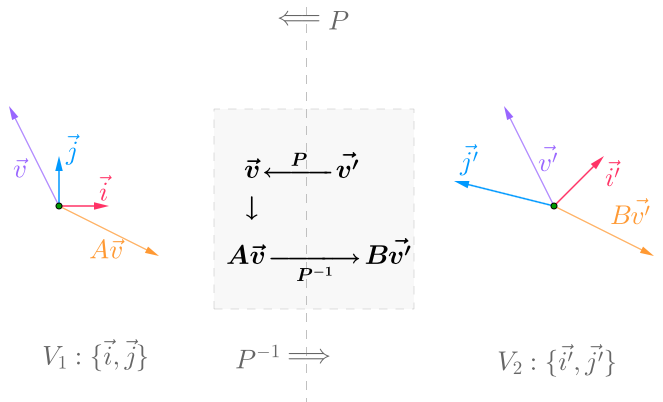
　　其中有两个基：V1 和 V2。V1 → V2，可以通过 P-1 转换；V2 → V1，可以通过 P 转换。

　　整个转换的核心，就是上图正中的文字：

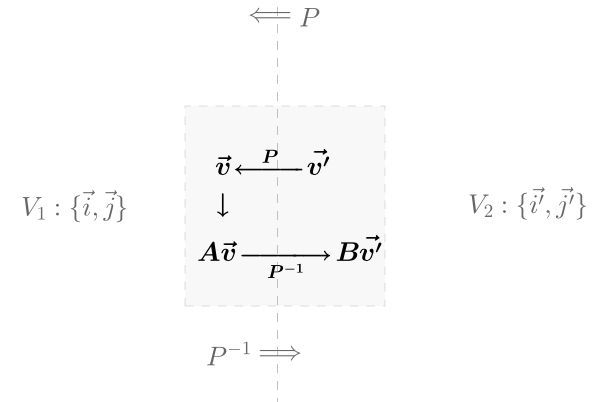
　　\vec{v'}是 V2 下的点，\vec{v'}通过 P 变为 V1 下的点，即 P\vec{v'}；在 V1 下，通过 A 矩阵完成线性变换，即AP\vec{v'}，通过 P-1 从变回  V2 下的点，即 P^{-1}AP\vec{v'}。

　　综上，我们有：

　　可以认为：

　　那么 B 和 A 互为相似矩阵。

　　为什么我们需要相似矩阵呢？比如这个 A 矩阵：

　　可以这样分解：

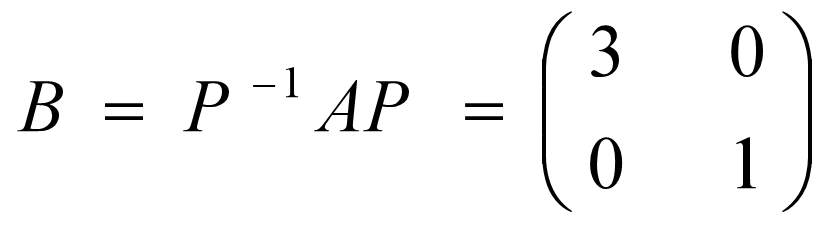
　　B 就是对角矩阵，看上去就很清爽，所以说相似变换就是坐标转换，转换到一个更方便计算的简单坐标系。

4 特征值分解

　　我们知道，对于矩阵 A 可以对角化的话，可以通过相似矩阵进行下面这样的特征值分解：

　　其中 Λ 为对角阵，P 的列向量是单位化的特征向量。(可以用定义推导出来)

　　拿个具体的例子来讲：

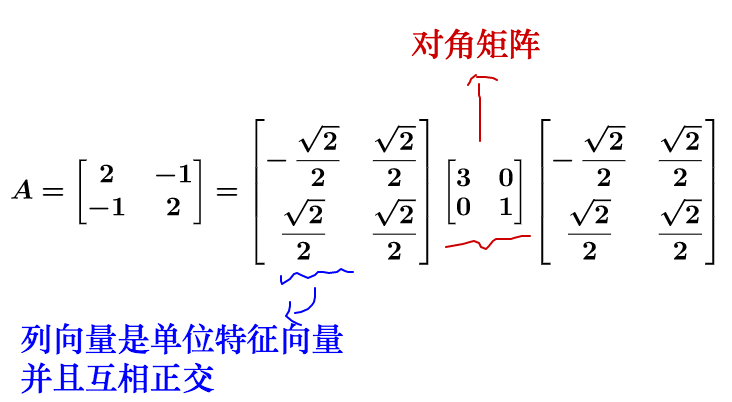
　　对于方阵而言，矩阵不会进行纬度的升降，所以矩阵代表的运动实际上只有两种：旋转和拉伸。最后的运动结果就是这两种的合成。

　　我们再回头看下刚才的特征值分解，实际上把运动给分解开了：

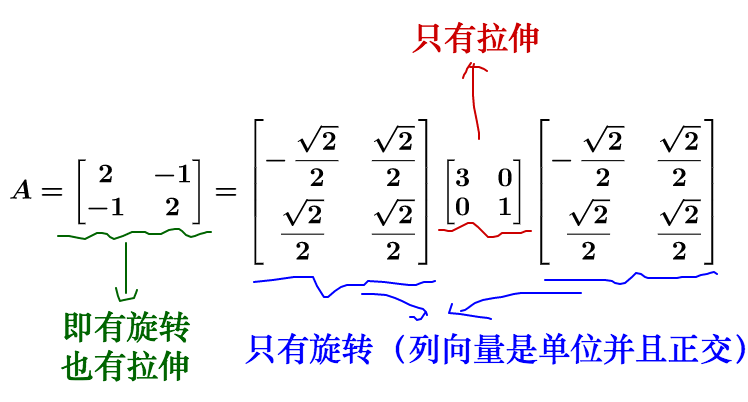
　　我们来看看在几何上的表现是什么，因此相似矩阵的讲解涉及到基的变换，所以大家注意观察基：

 　　左乘 P ：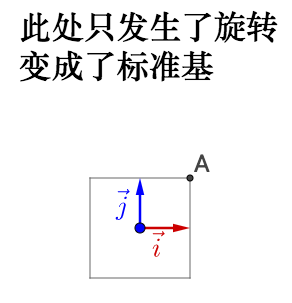

　　如果旋转前的基不正交，旋转之后变为了标准基，那么实际会产生伸缩，所以之前说的正交很重要。

　　继续左乘对角矩阵 Λ ：

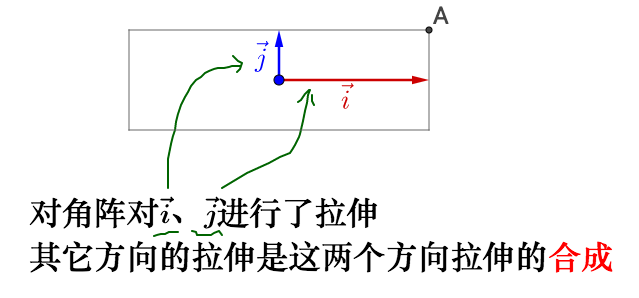
　　左乘 P-1 ：

　　相当于，之前的旋转指明了拉伸的方向，所以我们理解了：
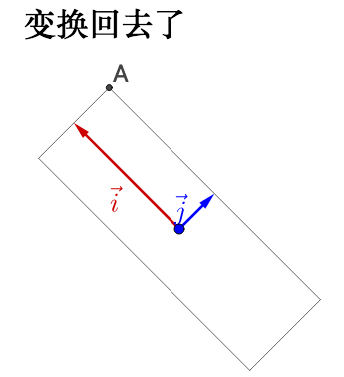
  • 特征值就是拉伸的大小
  • 特征向量指明了拉伸的方向

　　回到我们之前说的运动上去，特征值就是运动的速度，特征向量就是运动的方向，而其余方向的运动就由特征向量方向的运动合成。所以最大的特征值对应的特征向量指明了运动速度的最大方向。

　　但是，重申一下，上面的推论有一个重要的条件，特征向量正交，这样变换后才能保证变换最大的方向在基方向。如果特征向量不正交就有可能不是变化最大的方向。所以我们在实际应用中，都要去找正交基。但是特征向量很可能不是正交的，那么我们就需要奇异值分解了，这里就不展开了。

5 应用

 　　图片压缩：例如，有下面这么一副 512 × 512 的图片 (方阵才有特征值，所以找了张正方形的图) ：

　　这个图片可以放到一个矩阵里面去，就是把每个像素的颜色值填入到一个 512 × 512 的 A 矩阵中。

　　根据之前描述的有：

　　其中，Λ 是对角阵，对角线上是从大到小排列的特征值。

　　我们在 Λ 中只保留前面50个的特征值 (也就是最大的50个，其实也只占了所有特征值的百分之十) ，其它的都填0，重新计算矩阵后，恢复为下面这样的图像：

　　效果还可以，其实一两百个特征值之和可能就占了所有特征值和的百分之九十了，其他的特征值都可以丢弃了。

 

 

主要参考：如何理解相似矩阵？、如何理解矩阵特征值和特征向量？

posted @ 2020-08-21 18:17  sun-a  阅读(4205)  评论(0)  编辑  收藏  举报