向量和矩阵范数

向量的 1-范数、2-范数、无穷范数、p-范数；

矩阵的 1-范数、2-范数、无穷范数、L0范数、L1范数、L2范数、L21范数、核范数

1 向量范数

　　例：向量 X = [2，3，-5，-7 ]

1.1 向量的1-范数

　　向量各个元素的绝对值之和：

　　例：‖X‖₁ = 2+3+5+7 = 17

　　matlab代码：norm (X, 1)

1.2 向量的2-范数

　　向量各个元素的平方和再开方：

　　例：‖X‖₂ = (2×2+3×3+5×5+7×7)^1/2 = 9.3274

　　matlab代码：norm (X, 2)

1.3 向量的无穷范数

　　向量元素绝对值中的最大值：

　　例：‖X‖_+∞ = 7

　　matlab代码：norm (X, inf)

　　向量元素绝对值中的最小值：

　　例：‖X‖_-∞ = 2

　　matlab代码：norm (X, -inf)

1.4 向量的p-范数

　　其中 p ≥ 1，且存在：

2 矩阵范数

　　例：矩阵 A = [2，  3 ，-5，-7；

　　　　　　　　  4，  6 ， 8，-4；

　　　　　　　 　 6，-11，-3，16]

 2.1 矩阵的1-范数

　　矩阵每列元素绝对值之和中最大的值：

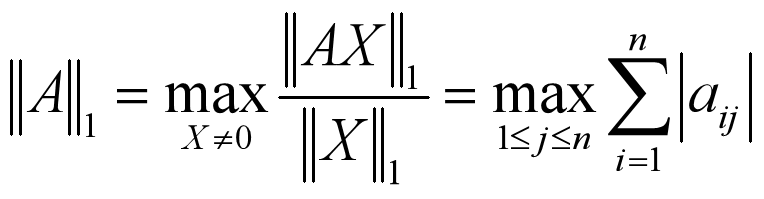
　　例：‖A‖₁ = 27

　　matlab代码：norm (A, 1)

 2.2 矩阵的2-范数

　　矩阵 A^TA 的最大特征值开方：

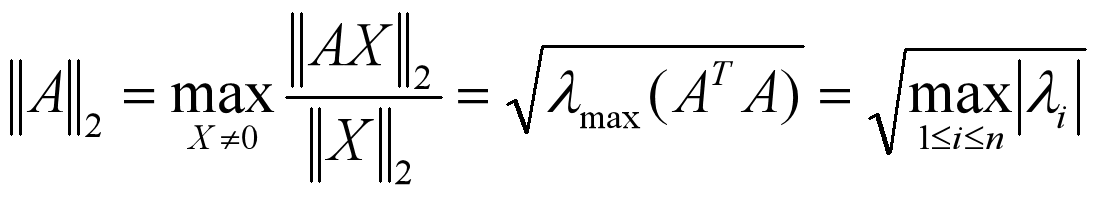
　　matlab代码：norm (A, 2)

 2.3 矩阵的无穷范数

　　矩阵每行元素绝对值之和中最大的值：

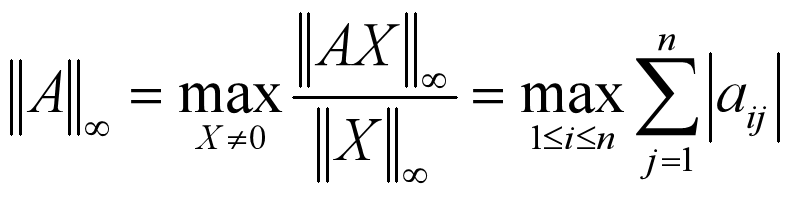
　　matlab代码：norm (X, inf)

//下面几个范数是机器学习中稀疏表示等地方常用到的，这些范数都是为了解决实际问题中的困难而提出的。

 2.4 矩阵的L0范数

　　矩阵的非0元素的个数，通常用它来表示稀疏，L0范数越小0元素越多，也就越稀疏。

 2.5 矩阵的L1范数

　　矩阵中的每个元素绝对值之和，它是L0范数的最优凸近似，因此它也可以近似表示稀疏，比L0更容易优化求解。

　　matlab代码：sum(sum(abs(A)))

 2.6 矩阵的L2范数

　　也叫做 F 范数，矩阵的各个元素平方之和再开平方根，它的优点在于它是一个凸函数，可以求导求解，易于计算。

　　matlab代码：norm(A,'fro');

 2.7 矩阵的L21范数

　　矩阵先以每一列为单位，求每一列的(向量)1-范数，然后再将得到的结果求(向量)2-范数，很容易看出它是介于L1和L2之间的一种范数。

　　matlab代码：norm(A(:,1),2) + norm(A(:,2),2) + norm(A(:,3),2)++ norm(A(:,4),2);

 2.8 矩阵的核范数

　　矩阵的奇异值之和，这个范数可以用来低秩表示（因为最小化核范数，相当于最小化矩阵的秩）。

　　matlab代码：sum(svd(A));