神经网络中的优化器 (tensorflow2.0)

在定义了损失函数之后，需要通过优化器来寻找最小损失，下面介绍一些常见的优化方法。

(BGD，SGD，MBGD，Momentum，NAG，Adagrad，Adadelta，RMSprop，Adam，Adamax，Nadam)

1 梯度下降法 (Gradient Descent，GD)

1.1 批量梯度下降法 (Batch Gradient Descent，BGD)

　　BGD 是梯度下降法最基础的形式，每次迭代更新中使用所有的训练样本，数学表达如下：

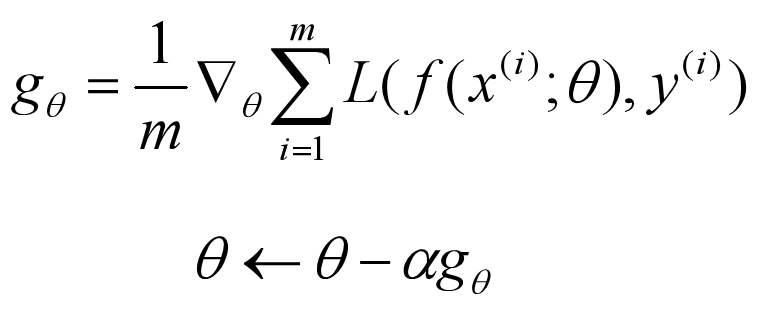
　　其中L为损失函数，m为训练样本个数，α为学习率。每次迭代，先对损失函数中的参数求导，再按照负梯度方向更新参数θ。

　　这样容易得到最优解。但每迭代一次，需要用到训练集中的所有数据，如果数据量很大，那么迭代速度就会非常慢。

1.2 随机梯度下降法 (Stochastic Gradient Descent，SGD)

　　SGD 每次迭代中使用的是单个训练样本，数学表达如下：

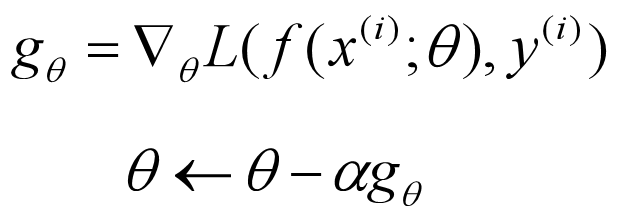
　　SGD 每次迭代只使用一个样本，如果训练集很大，可能只使用其中一部分就能把参数θ迭代到最优解了。但是，SGD容易受噪声影响，并不是每次迭代都向整体最优化方向进行。

　　训练速度快，迭代次数多，在解空间的搜索过程中看起来很盲目。

1.3 小批量梯度下降法 (Mini-Batch Gradient Descent，MBGD)

　　MBGD 中和了 BGD 和 SGD 方法，每次迭代使用 batch_size 个训练样本，数学表达如下：

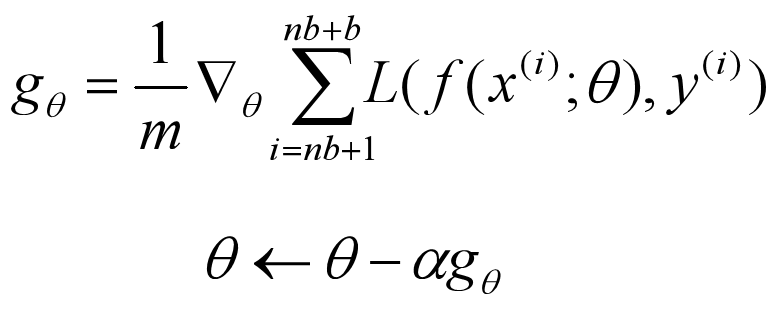
　　其中 n 表示第 n+1 次迭代，b 表示 batch_size (b=1，就是SGD；b=m，就是BGD)，batch_size 一般设置为2的次方数，如16、32、64、128等，可以根据自己的 GPU 或 CPU 大小来设置。

　　因为每次迭代使用多个样本，所以 MBGD 比 SGD 收敛更稳定，也能避免 BGD 在数据集过大时迭代速度慢的问题。如果训练集本来就不大，直接使用 BGD 就可以了。

1.4 梯度下降法存在的问题

　　（1）对于非凸函数可能会陷入局部极小值。此外，还可能会被困在鞍点 (所有维度的梯度在这附近都接近于0，损失函数变化慢)，如果是 BGD，可能会停止不动，如果是 MBGD 或者 SGD，因为每次找到的梯度不同，可能会发生震荡，来回跳动。

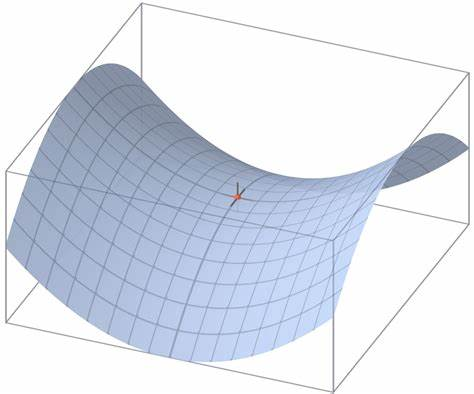
　　（2）SGD 很容易被困在沟壑 (ravine) 中，即一个维度上的曲线比另一个维度的曲线陡的多。在这种情况下，SGD 在沟壑的斜坡上震荡。

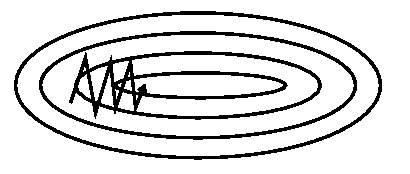
　　（3）学习率的选择问题。学习率太小，收敛速度慢；学习率太大，可能会在最优点附近震荡无法收敛。

　　（4）对所有参数使用了相同的学习率。对于一些稀疏的数据或者特征，我们希望能更新的更快些。

2 动量算法 (Momentum algorithm)

2.1 Momentum

　　momentum 改进自 SGD算法，让每一次参数更新方向不仅仅取决于当前位置的梯度，还受到上一次参数更新方向的影响，数学形式如下：

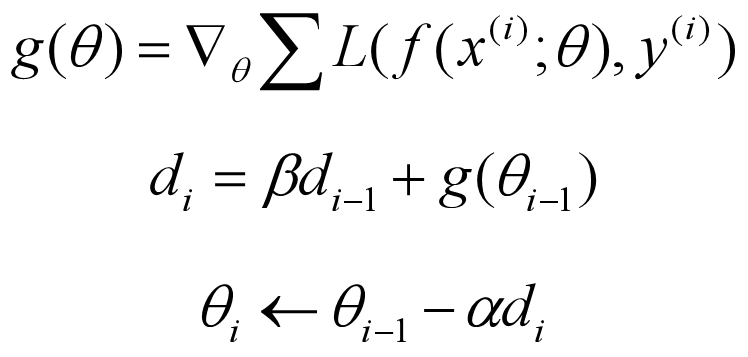
　　其中，d_i 和 d_i-1 分别是这一次和上一次的更新方向，β 是对上一次更新方向的衰减权重，一般在0~1之间。

　　momentum 想法很简单，就是通过之前迭代的更新量，来平滑这一次迭代的梯度方向。从物理的角度来看，就像是一个小球滚落时会受到自身历史动量的影响，因此就能更平稳、快速的冲向局部最小点。

2.2 Nesterov Accelerated Gradient (NAG)

　　NAG 是对传统 momentum 方法的一项改进，NAG 认为 “既然我已经知道这次要多走 αβd_i-1 的量 (注意 momentum 中的数学表达)，那我直接先走到 αβd_i-1 之后的地方，再根据那里的梯度前进不是更好吗？”，所以就有了下面的公式：

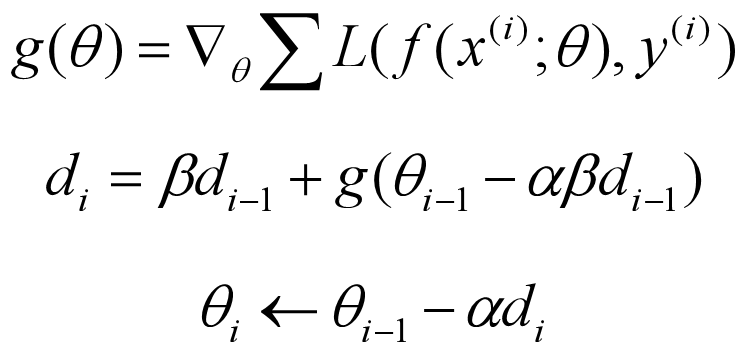
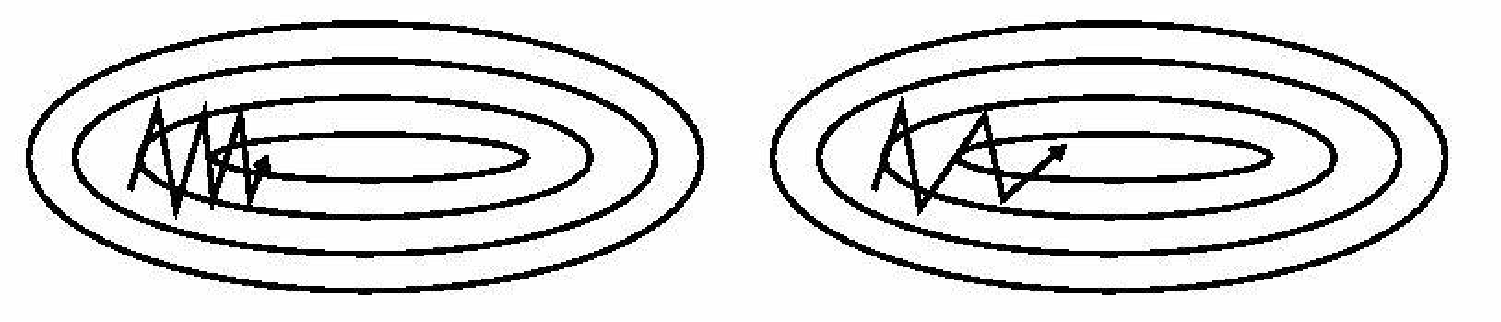
　　直观上看是这样的，momentum 首先计算一个梯度 (短的蓝色向量)，然后在加速更新梯度的方向进行一个大的跳跃 (长的蓝色向量)，nesterov项首先在之前加速的梯度方向进行一个大的跳跃 (棕色向量)，计算梯度然后进行校正 (绿色梯向量)。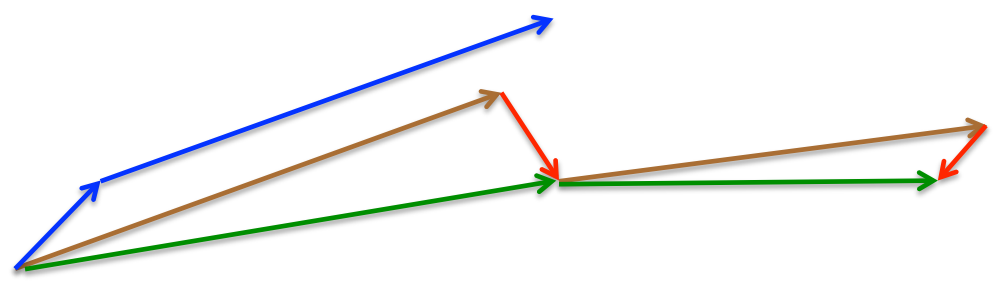

　　NAG 的收敛速度比 momentum 更快，许多文章解释为：能够让算法提前看到前方的地形梯度，如果前面的梯度比当前位置的梯度大，那我就可以把步子迈得比原来大一些，如果前面的梯度比现在的梯度小，那我就可以把步子迈得小一些。这个大一些、小一些，都是相对于原来不看前方梯度、只看当前位置梯度的情况来说的。有篇文章给出了另一种更具体的解释：NAG 本质上是多考虑了目标函数的二阶导信息，所谓“往前看”的说法，在牛顿法这样的二阶方法中也是经常提到的，比喻起来是说“往前看”，数学本质上则是利用了目标函数的二阶导信息。

2.3 动量算法的优点

　　（1）明显改善了梯度下降法中的问题(2)，即在沟壑的斜坡上震荡，使收敛更平滑。

　　（2）对于学习率也有一定的改善。在学习率较小的情况下，收敛速度慢，但更新方向基本不变，动量算法中的 d_i就会不断叠加、增大，从而加快收敛；学习率较大的时候，会在最优点附近震荡，更新方向在不断变化，d_i就会叠加减小，在一定程度上减轻了震荡。（当然，要更好地改善学习率的问题，更推荐后面的自适应学习率的优化方法）

3 自适应学习率算法

3.1 自适应梯度算法 (Adaptive gradient algorithm，Adagrad）

　　Adagrad 对低频的参数做较大更新，对高频的参数做较小的更新，因此，该算法对于稀疏数据的表现很好，极大的提高了 SGD 的健壮性。数学表达如下：

　　其中 ε 是一个避免零除的平滑项，如取值1e-8。

　　可以看出，随着迭代次数增加，S_i 逐渐变大，就会对学习率产生一个约束。改善了梯度下降法中的问题(3)，使得参数更新前期变化大，后期变化小。也改善了问题(4)，因为稀疏数据 S_i 积累较少，更新更快。

　　主要缺点也在于分母中平方梯度的积累，随着 S_i 不断增加，学习率收缩，最终变得无穷小，导致模型无法再训练，接下来的 Adadelta 算法就是解决这个问题的。

3.2 Adadelta

　　Adadelta 是对 Adagrad 的扩展，最初方案依然是对学习率进行自适应约束。Adadelta 不会累积过去所有的平方梯度，而是过去所有的平方梯度的衰减平均值。即：

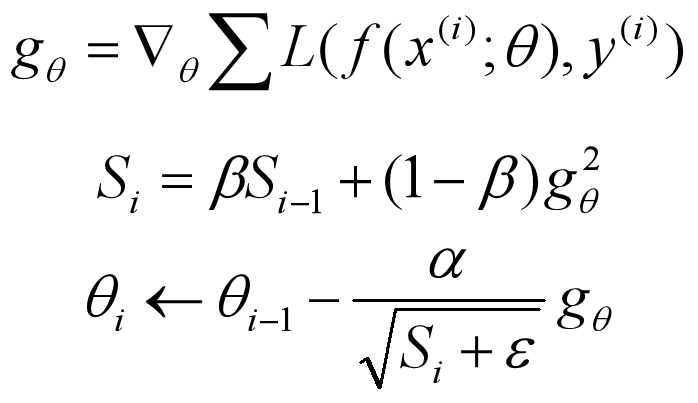
　　这里的 β 和 momentum 中的 β 没有关系，是另一个超参数。由于分母相当于梯度的均方根 (RMS)，所以可以用 RMS 简写上式如下：

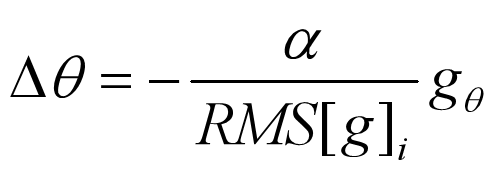
　　论文作者认为，更新应该具有与参数相同的假设单位，所以他们首次定义另一个指数衰减平均值，这次，不是平方梯度，而是平方参数更新，如下式：

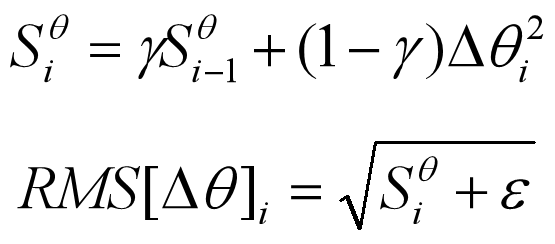
　　由于 RMS[Δθ]_i 是未知的，我们用上一时刻的参数更新的 RMS 近似它，所以我们用 RMS[Δθ]_i-1 来替换学习率,最终得到 Adadelta 更新规则如下：

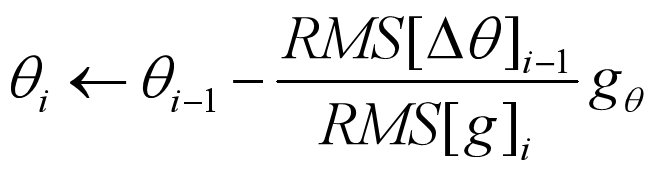
　　这里甚至不需要设置默认的学习率。

　　训练初中期，加速效果不错，很快；训练后期，反复在局部最小值附近抖动。

3.3 RMSprop

　　RMSprop 和 Adadelta 算法一样，都是为了解决 Adagrad 算法急剧下降的学习率的算法，RMSprop 与 Adadelta 的第一种形式相同，这两个算法是同一时间独立开发的，公式如下：

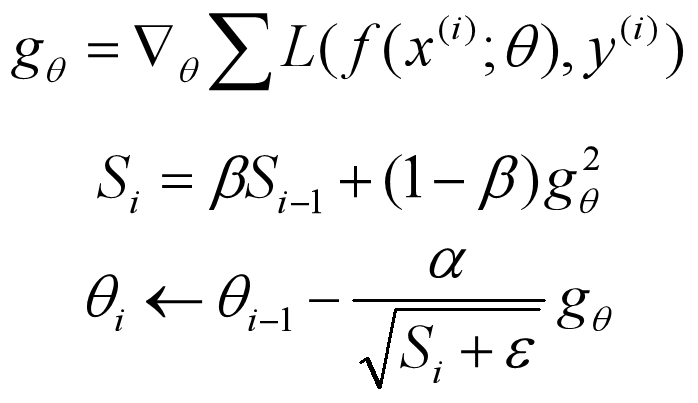
　　一般 β 设置为 0.9，学习率 α 设置为 0.001。

　　 RMSprop 依然依赖于全局学习率；属于 Adagrad 的一种发展，Adadelta 的变体，效果趋于二者之间；适合处理非平稳目标；对于RNN效果很好。

3.4 自适应矩估计 (Adaptive Moment Estimation，Adam)

　　Adam 是另一种参数自适应学习率的方法，相当于 RMSprop + Momentum，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。公式如下：

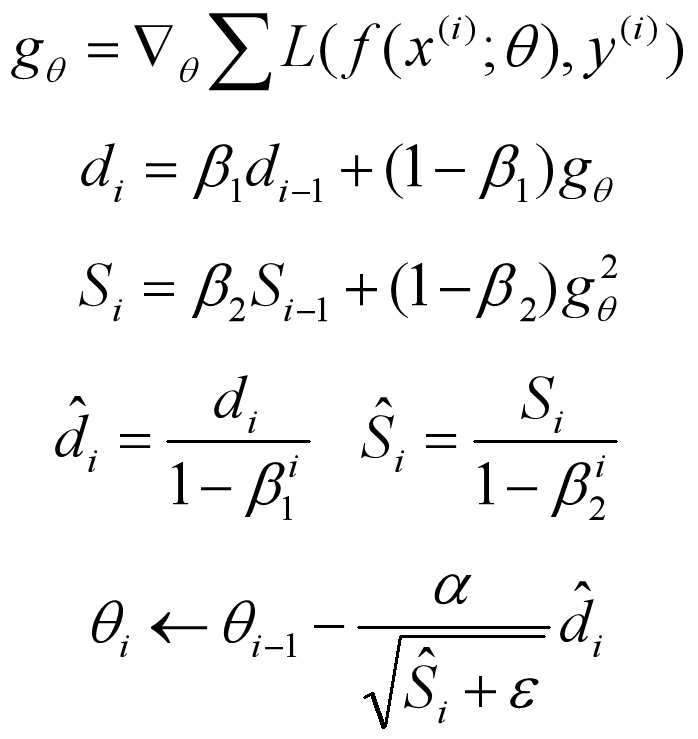
　　ˆd_i 和 ˆS_i 是对 d_i 和 S_i 的偏置校正(Bias Correction)，调整前期的误差，这样可以近似为对期望的无偏估计。一般情况下，β₁ 设置为0.9，β₂ 设置为0.999，ε 设置为1e-8。

　　Adam 适用于大多非凸优化，适用于大数据集和高维空间。

3.5 Adamax

　　Adamax 是 Adam 的一种变体，该方法对学习率的上限提供了一个更简单的范围。公式如下：

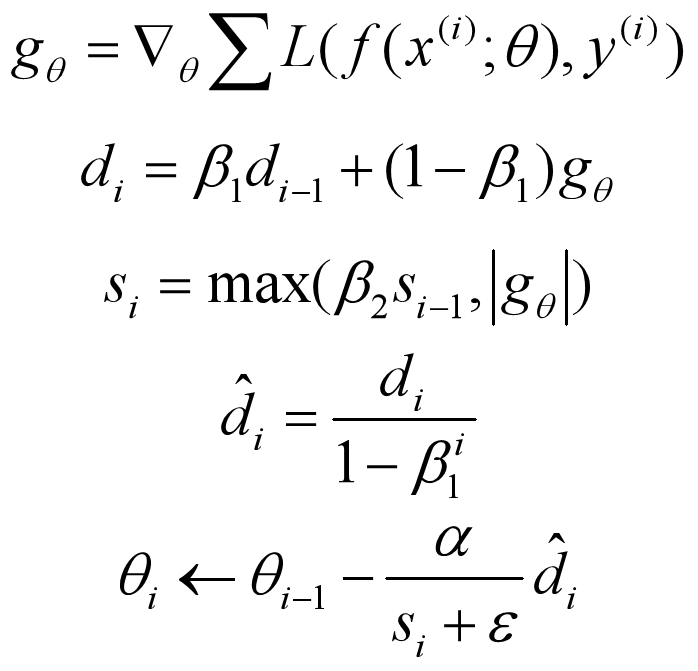
　　可以看出，Adamax 学习率的边界范围更简单。

3.6 Nadam

　　Nadam 类似于带有 Nesterov 动量项的 Adam。公式如下：

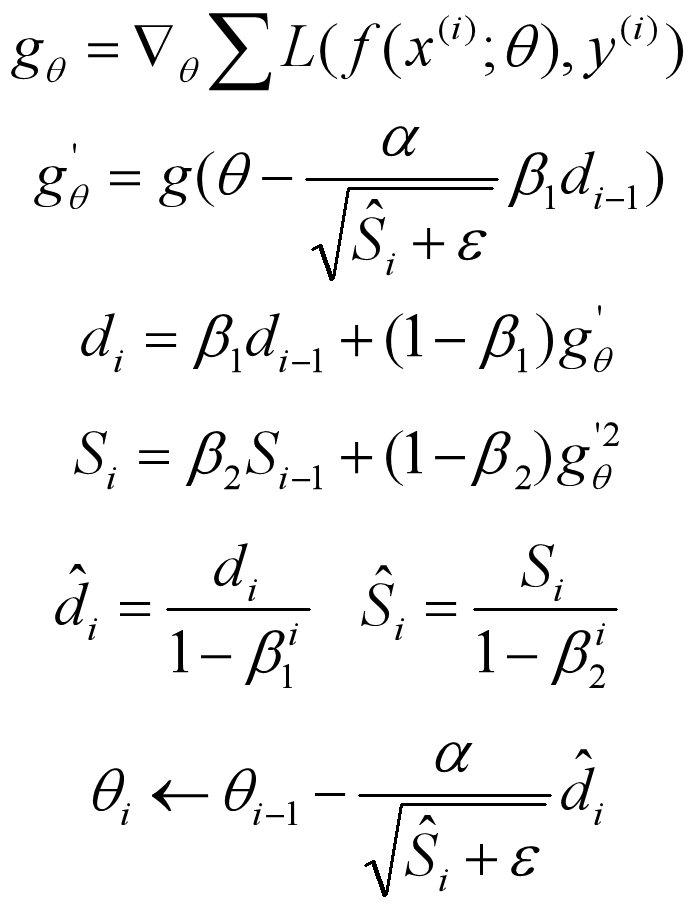
　　Nadam 对学习率有了更强的约束，同时对梯度的更新也有更直接的影响。一般而言，在想使用带动量的 RMSprop，或者 Adam 的地方，大多可以使用 Nadam 取得更好的效果。

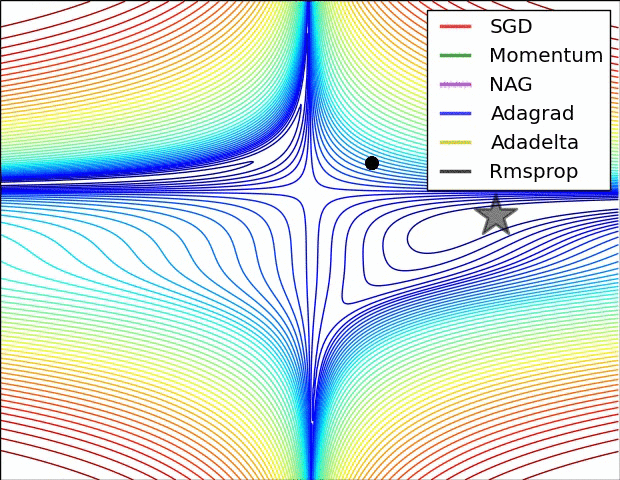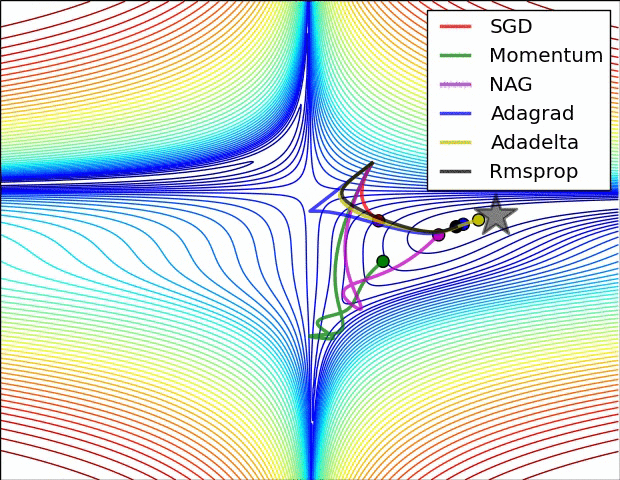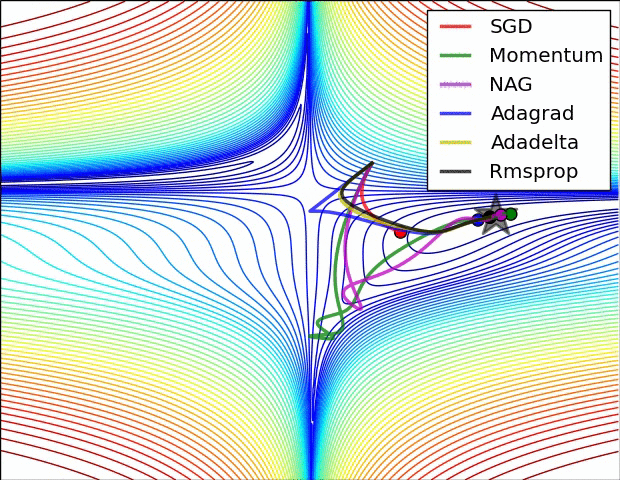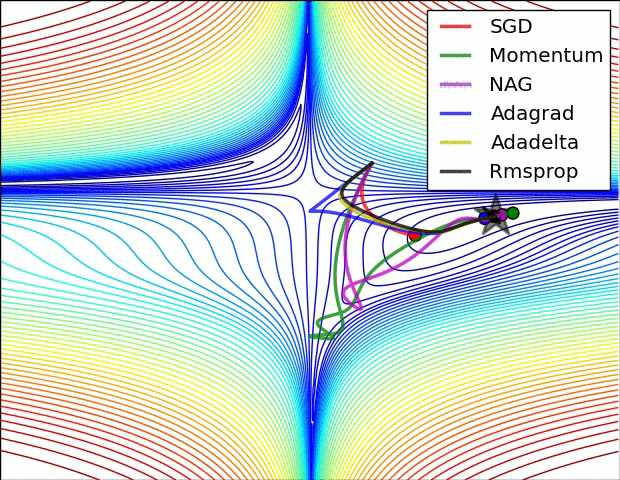
4 可视化

　　更多内容可参考该链接。

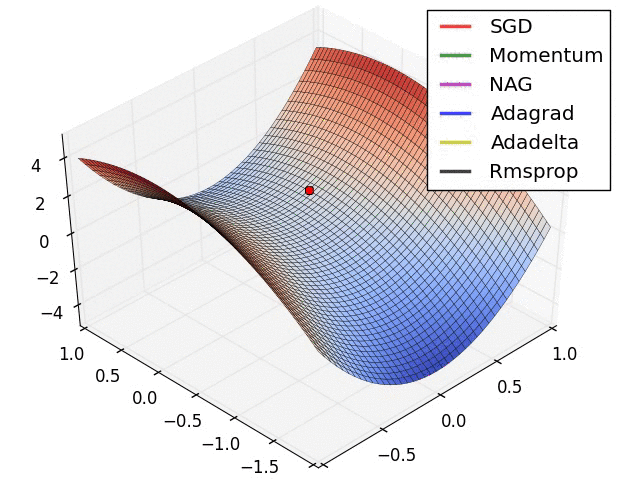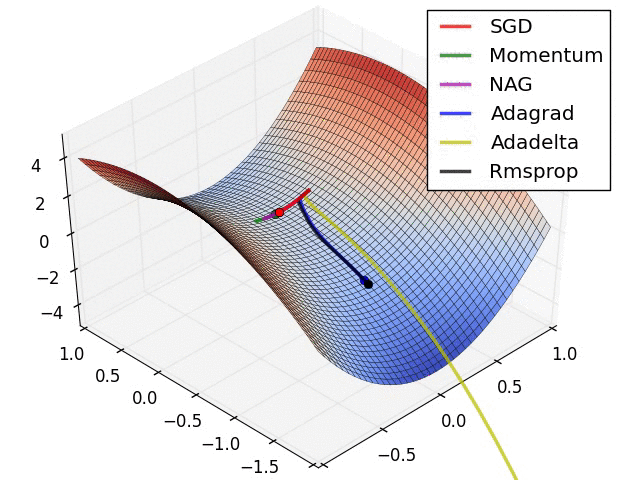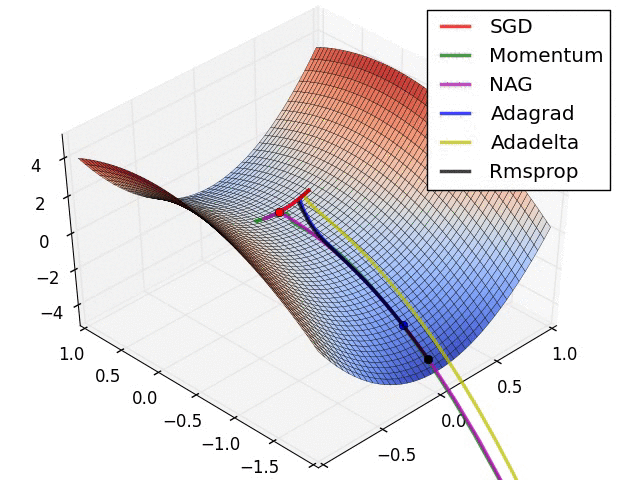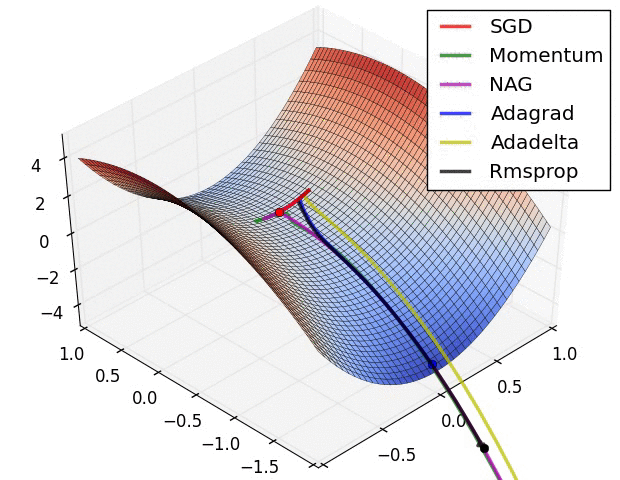
5 tensorflow2.0 提供的优化器

　　tensorflow2.0 官方文档中提供了下面几类优化器：

tf.keras.optimizers.SGD(
    learning_rate=0.01, momentum=0.0, nesterov=False, name='SGD', **kwargs
)

该函数实现的是 MBGD，在训练神经网络时，可以设置 batch_size 的大小，batch_size=1，就是SGD；batch_size=m，就是BGD。

参数 momentum 决定动量项，当 momentum == 0 时，就是简单的梯度下降法。

参数 nesterov 决定是否使用 nesterov 动量项。

tf.keras.optimizers.Adagrad(
    learning_rate=0.001, initial_accumulator_value=0.1, epsilon=1e-07,
    name='Adagrad', **kwargs
)

initial_accumulator_value 是 S_i 的初始值，必须是非负的。

tf.keras.optimizers.Adadelta(
    learning_rate=0.001, rho=0.95, epsilon=1e-07, name='Adadelta', **kwargs
)

tf.keras.optimizers.RMSprop(
    learning_rate=0.001, rho=0.9, momentum=0.0, epsilon=1e-07, centered=False,
    name='RMSprop', **kwargs
)

tf.keras.optimizers.Adam(
    learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=False,
    name='Adam', **kwargs
)

tf.keras.optimizers.Adamax(
    learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, name='Adamax',
    **kwargs
)

tf.keras.optimizers.Nadam(
    learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, name='Nadam',
    **kwargs
)

$\hat{n_{t}}$

posted @ 2020-07-29 17:42 sun-a 阅读(6636) 评论(0) 编辑收藏举报

刷新页面返回顶部

sun-a