优化深层神经网络
超参数调试、正则化等
1. 数据集的分配
Train / Dev / Test sets 训练集、验证集、测试集
要确保训练集和测试集的数据符合同分布
eg:
小数量样本：60% / 20% / 20%
大数据：99.5% / 0.4% / 0.1%
2. 偏差(bias)、方差(variance)
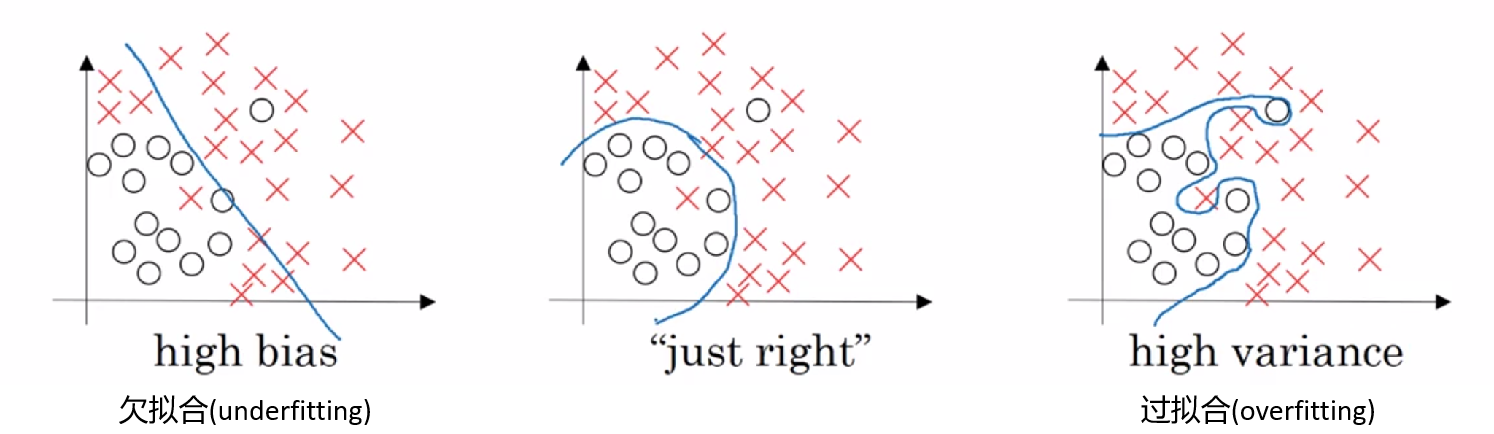
可能的情况
我们希望得到一个低偏差、低方差的结果。
3. 正则化(Regularization)
正则化可以解决高方差，即过拟合的问题。“权重衰减”
L2正则化：
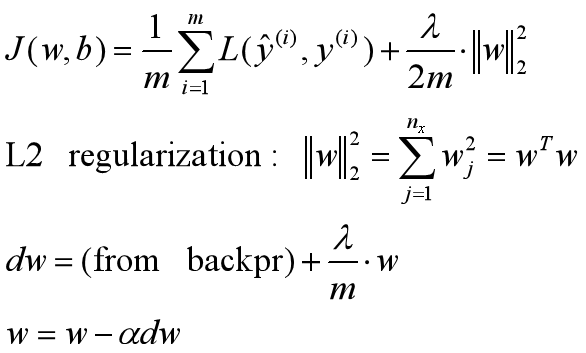
Dropout正则化：每个节点都有被保留和消除的概率，对于每个训练样本，都会采用一个精简后的神经网络来训练
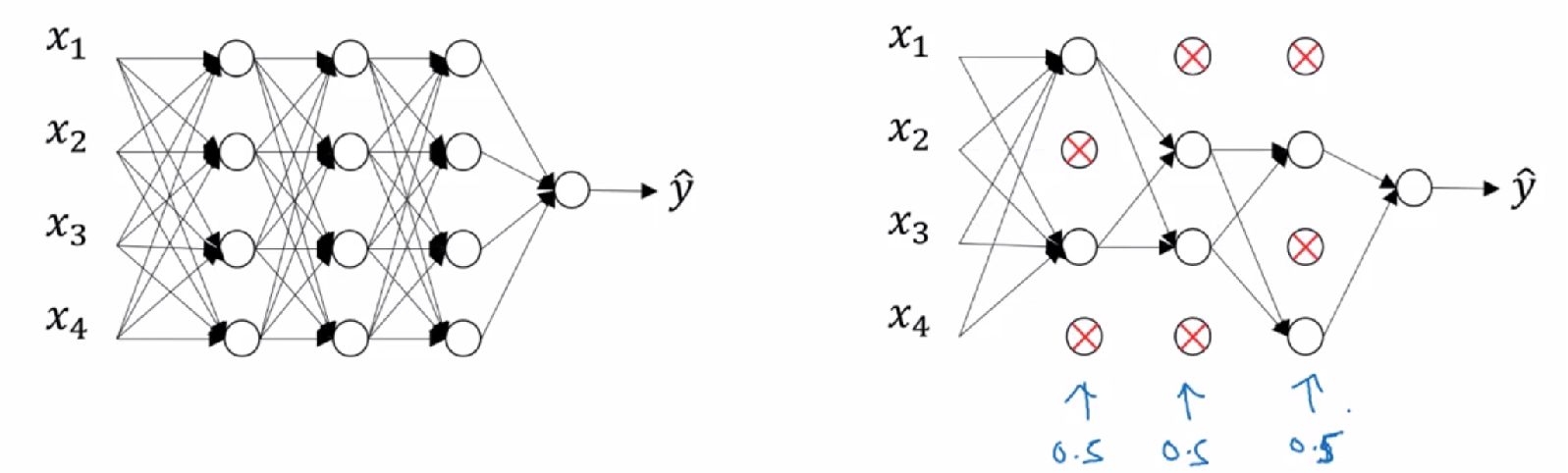
反向随机失活(Inverted dropout)：
#伪代码示例
keep_prob = 0.8
d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep_prob
a3 = np.multply(a3,d3)
a3 = a3 / keepz_prob
- 这样的方式会使网络不能依赖任何某一个特征，因为特征有可能被随机清除，所以需要通过这个方式积极的传播开，drop-out 也将产生说所权重得平方范数得效果
- 如果担心某些层比其他层更容易发生过拟合，可以把该层的 keep-prod 值设置的更低，缺点是有更多的超参数
其他防止过拟合的方法：增加数据量，提前结束迭代等
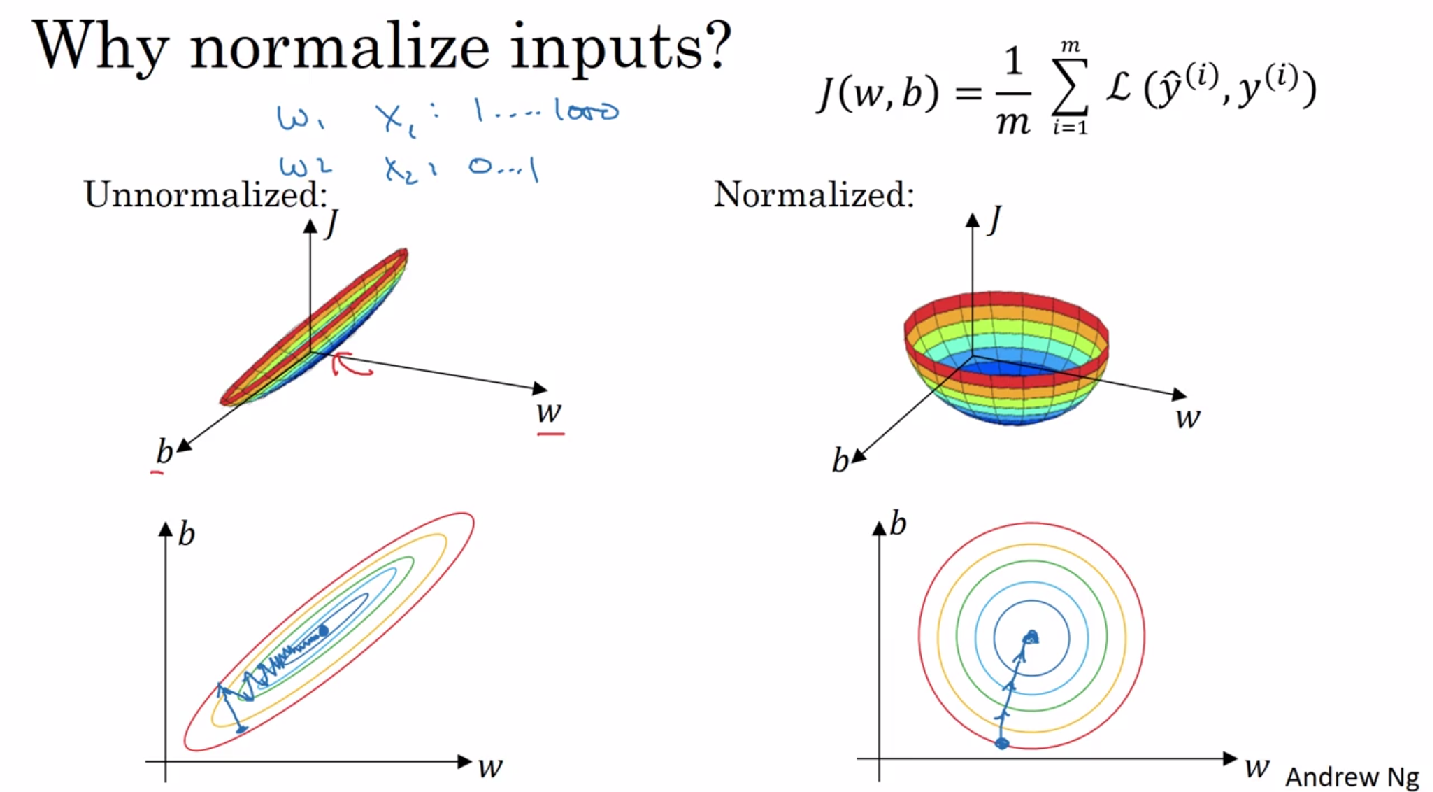
4. 归一化输入
为了使特征在相似范围里，更容易优化损失函数
第一步，零均值化；第二步，归一化方差
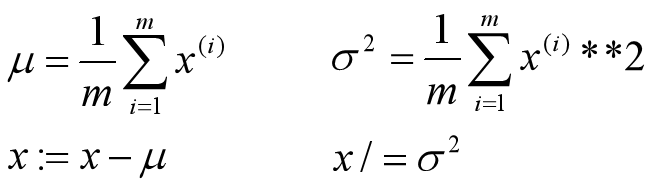
5. 梯度消失或梯度爆炸(Vanishing / exploding gradients)
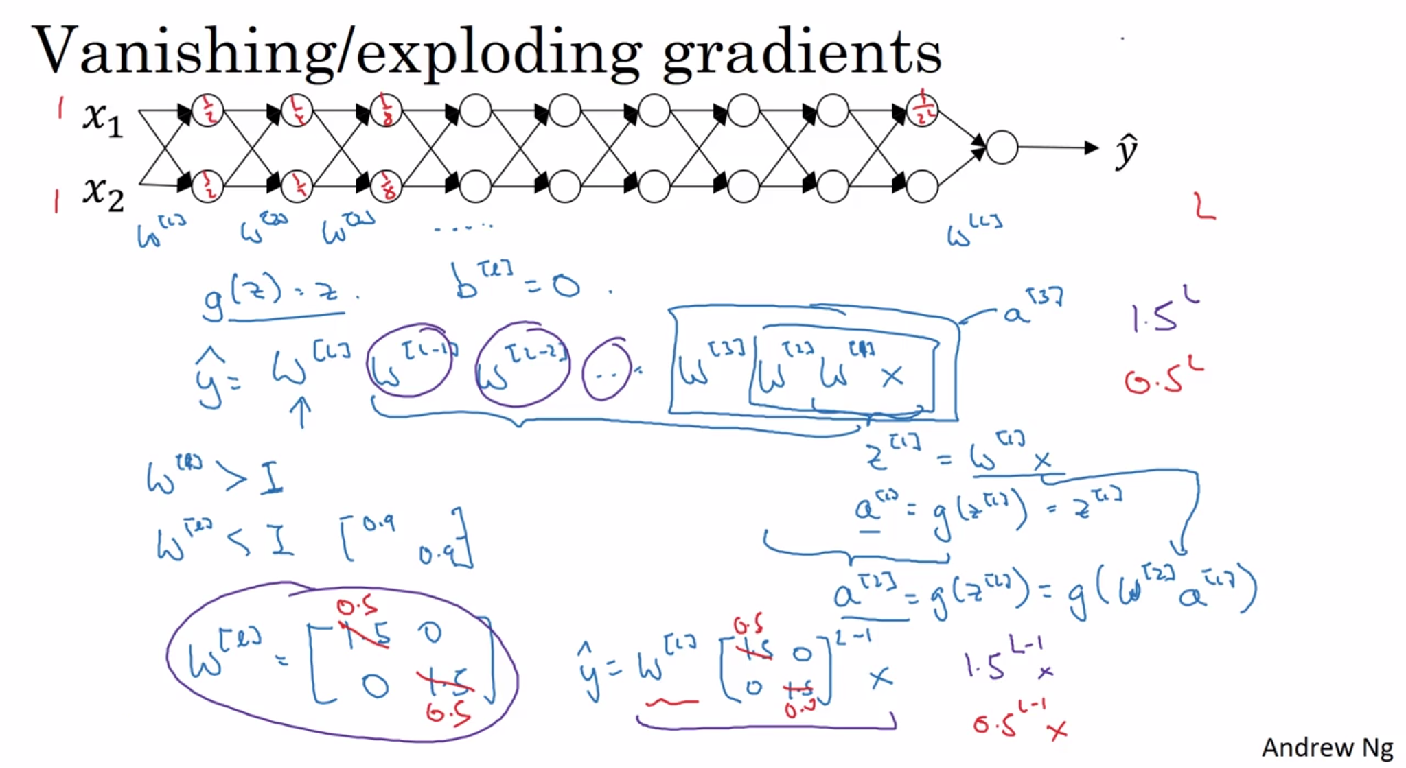
假设激活函数g(Z)=Z，b=0，如果权重 W比“1”大一点，例如“1.5”，激活函数就会出现指数级增长；比“1”小一点，例如“0.5”，激活函数就会出现指数级下降，相对应L层的其他超参数也会出现指数级的变化。假设有150层，而梯度下降的步长会特别小，那么训练周期会特别长。
解决梯度消失或爆炸：权重初始化
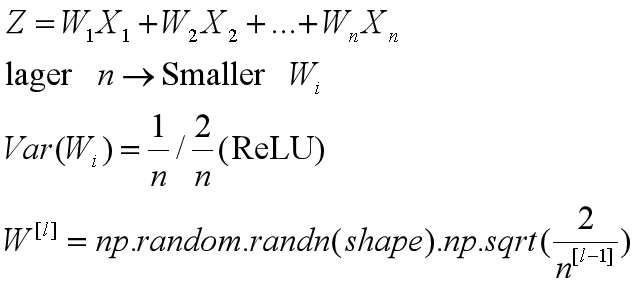
6. 梯度检验(gradient checking)
确保反向传播正确实施。梯度的数值逼近：
梯度检验：
- 不要在训练中使用梯度检验，只用于调试
- 如果算法的梯度检验失败，要检查所在项
- 如果有正则化，要注意正则项
- 不能和 dropout 同时使用
7. Mini-batch 梯度下降法
数据集过大时每次迭代需要消耗大量时间，Mini-batch 将数据集分为多个小组（例如：500百万个数据分为5000组一组一千个），对每个组进行迭代。
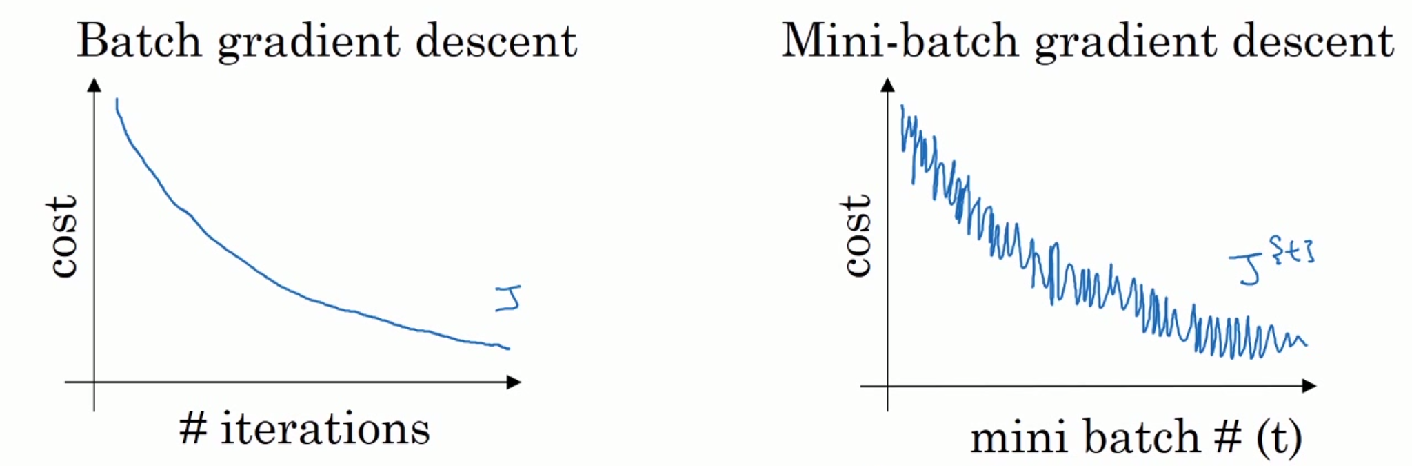
训练迭代图：
mini-batch 的大小：mini-batch大小等于样本总数“m”时，相当于只有一组；mini-batch大小等于“1”的 时候，相当于有m组。选取的值应该在1~m之间，常见的大小有26、27、28、29，最好在CPU、GPU的存储范围内。
当样本集较小时，没必要使用mini-batch。
8. 指数加权平均 (exponentially weighted averages)
以London一年的温度分布为例：
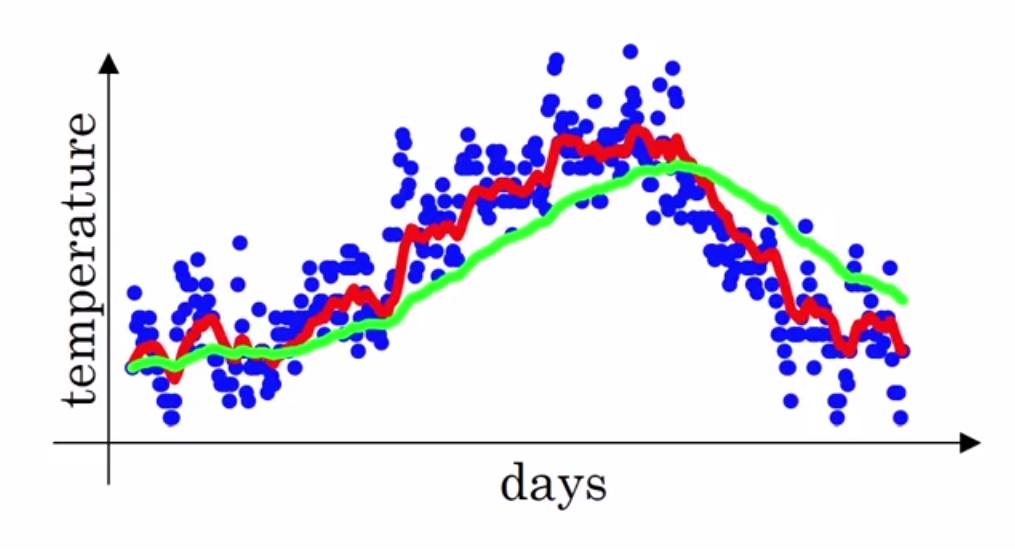
线条是按照加权平均来计算的温度值：
其中β的值在实际中一般取0.98，就是绿线，此时就是V0的值为实际记录值。
偏差修正(Bias Correction)：
实际上，在用公式推导的时候V0=0，需要利用偏差修正调整前期的误差，使其达到更吻合的绿线。计算如下：
在实际应用中，大多不在乎初期的误差，会拿偏差的估测继续计算下去，因为后面的拟合度也不差。
9. 其他加速梯度下降的方法
动量梯度：
在纵向上，需要尽可能的缩小摆动，横向上，尽可能加快速度，公式如下：
在实际中β的值多为0.9，一般也不用修正偏差，因为迭代增加到10后，影响就不大了，有些参考资料中会删去1−β，然后修改学习率的值来调节，Andrew Ng更偏向于不删，效果差不多。
RMSProp(均方根)：
假设在纵轴是b,横轴是W(这样假设的理由是，只要b减小，上下的摆动就会减小，而只要W增大，梯度下降的速度也就增快了)
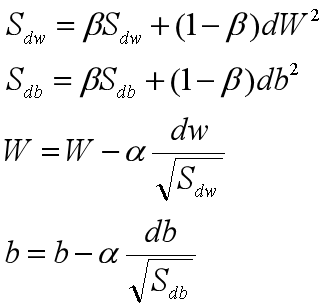
其中dw变小，相应最后W变大，而db相反，这样就减小了摆动。而在实际操作中为了防止分母趋于0，会加上一个很小的数：
Adam优化算法：
相当于结合了Momentun和RMSProp
Hyperparameters choice：α(needs to be tune)、β1(0.9 、dw）、β2(0.999 、dw2）、ϵ(1e-8)
10. 学习衰减率 (Learning rate decay)
在训练的过程中，大的“步伐”会在最优值附近大幅度的“徘徊”，在训练的后期，小的学习率有利于减小这一幅度，如图（绿线运用了学习衰减率）：
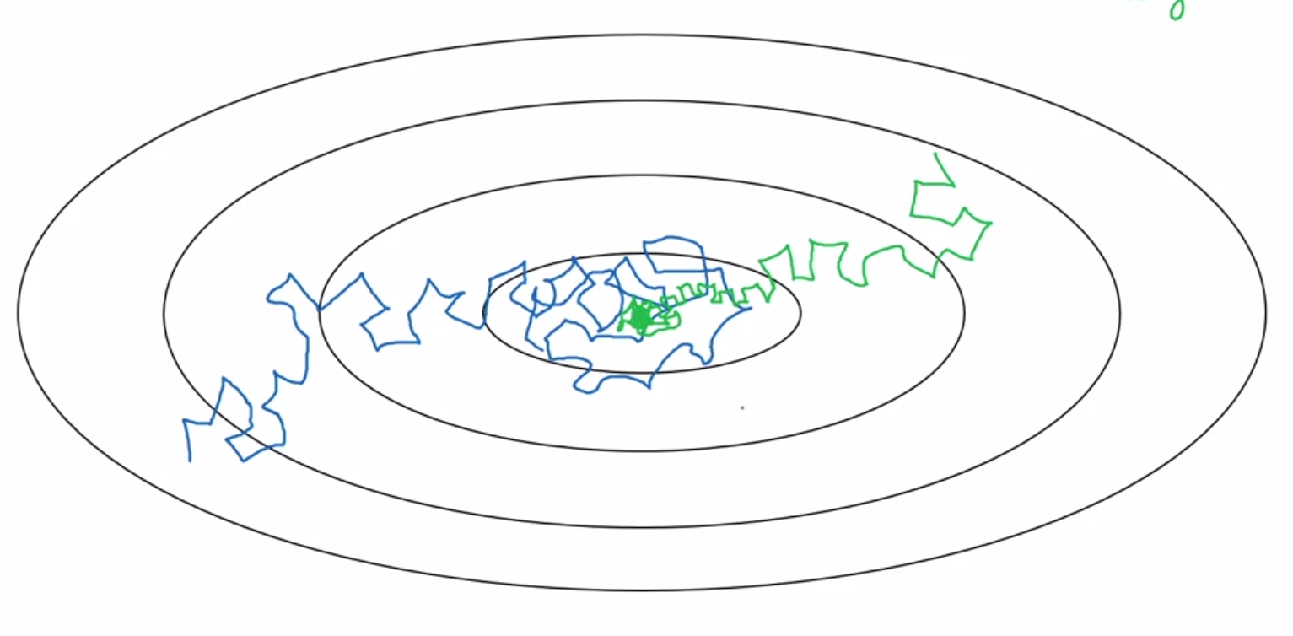
实现方法：
还有其他的更多的方法来实现，效果也不同
11. 超参数调试
- 随机选择点，因为参数多，很难提前知道哪个超参数最重要
- 从粗糙到精确，在最好的区域更密集地取值
选择合适的标尺：
- 在对数轴均匀取值，而不是标准轴。例如：0.0001-0.1（0.0001、0.001、0.01、1）
- 在某些情况用其他形式。例如：β（0.9-0.999），计算1-β（0.1-0.001）
如何搜索合适的参数：
- 直接调整一个模型
- 并行训练多个模型(计算资源足够)
12. Batch Norm
normalize 每层的输入z (归一化、标准化)，加速学习。根据需求，参数 γ，β 可用于缩放
神经网络中使用：
13. Softmax 回归
可以将用于二分类的逻辑回归用于多分类
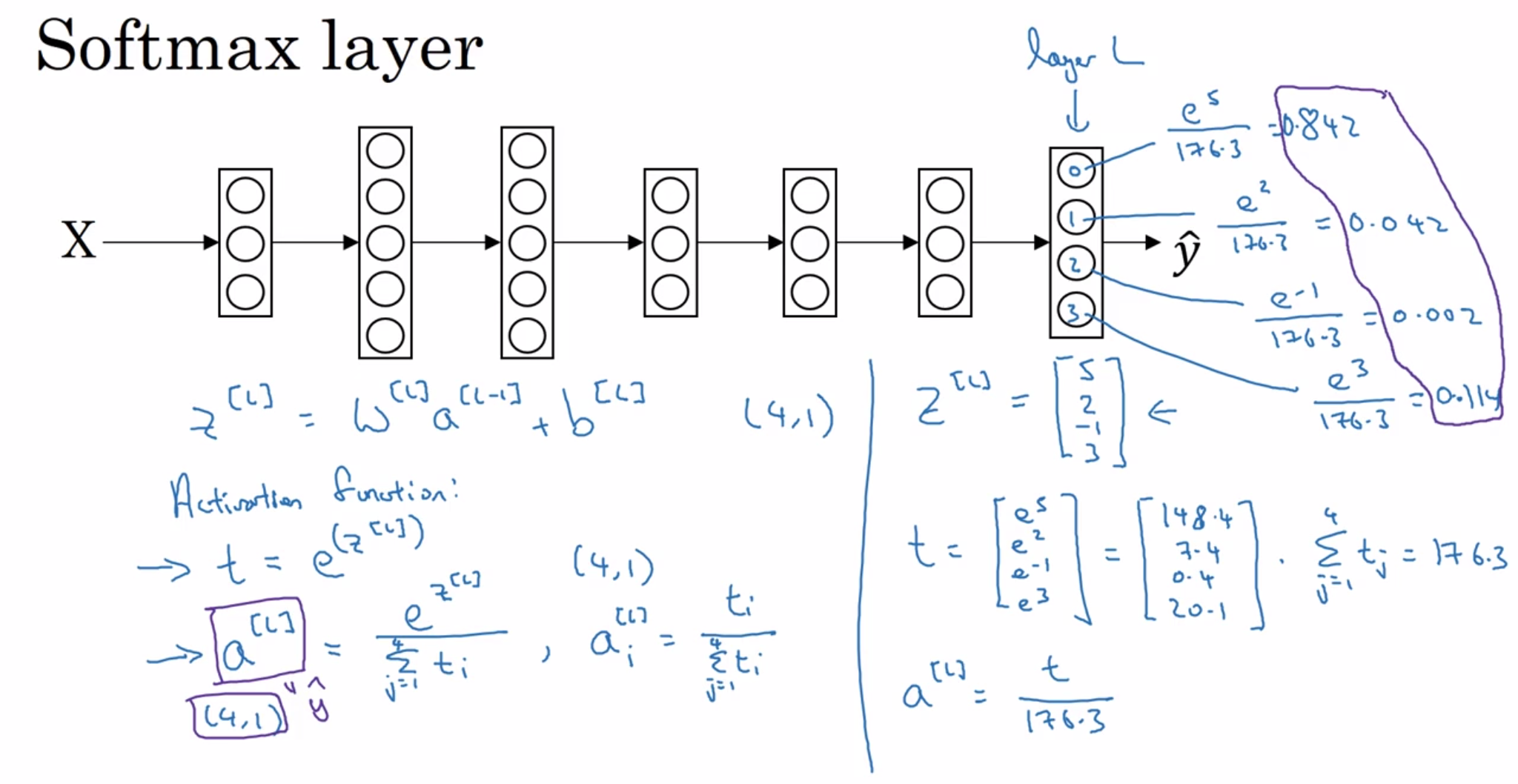
以上内容主要是对吴恩达《深度学习》课程第二课的总结
