《神经网络的梯度推导与代码验证》之LSTM的前向传播和反向梯度推导

前言

在本篇章，我们将专门针对LSTM这种网络结构进行前向传播介绍和反向梯度推导。

关于LSTM的梯度推导，这一块确实挺不好掌握，原因有：

一些经典的deep learning 教程，例如花书缺乏相关的内容
一些经典的论文不太好看懂，例如On the difficulty of training Recurrent Neural Networks上有LSTM的梯度推导但看得我还是一头雾水（可能是我能力有限。。）
网上关于LSTM的梯度推导虽多，但缺少保证其正确性的验证实验

考虑到上述问题，本篇章将以最低限度的知识依赖进行LSTM的反向梯度推导，所有推导基础均基于《神经网络的梯度推导与代码验证》之数学基础篇：矩阵微分与求导。为保证所得无误，后续将通过tensorflow的自动微分工具验证LSTM梯度推导结论的准确性。另外，为节约体能，推导过程相对没那么详细，因为这实际上只是反复应用矩阵微分与求导的原理而已，手把手教学级的内容请参考数学基础篇：矩阵微分与求导。

更多相关内容请见《神经网络的梯度推导与代码验证》系列介绍。

后续会反复出现$\boldsymbol{\delta}^{l}$这个（类）符号，它的定义为$\boldsymbol{\delta}^{l} = \frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l}}}$，即loss $l$对$\boldsymbol{z}^{\boldsymbol{l}}$的导数
其中$\boldsymbol{z}^{\boldsymbol{l}}$表示第$l$层（DNN，CNN，RNN或其他例如max pooling层等）未经过激活函数的输出。
$\boldsymbol{a}^{\boldsymbol{l}}$则表示$\boldsymbol{z}^{\boldsymbol{l}}$经过激活函数后的输出。

这些符号会贯穿整个系列，还请留意。

5.1 LSTM的前向传播

在RNN模型里，我们讲到了RNN具有如下的结构，每个序列索引位置$t$都有一个隐藏状态$\boldsymbol{h}^{(t)}$。

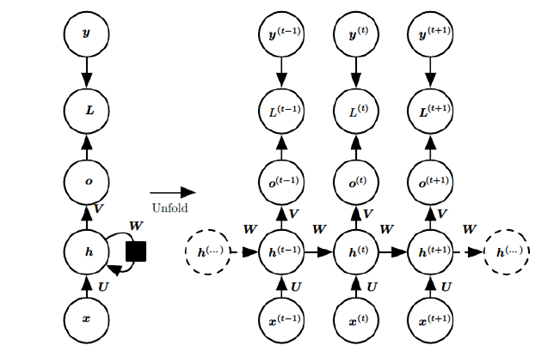
如果我们只关注RNN的核心循环部分而不看$\boldsymbol{o}^{(t)}$，$\boldsymbol{L}^{(t)}$和$\boldsymbol{y}^{(t)}$，则RNN的模型可以简化成如下图的形式：

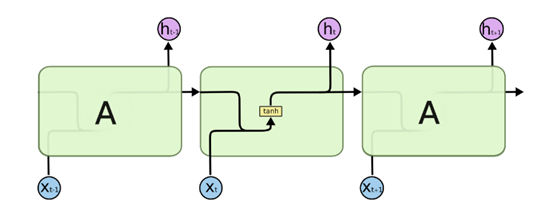
图中可以很清晰看出在隐藏状态$\boldsymbol{h}^{(t)}$由$\boldsymbol{x}^{(t)}$和$\boldsymbol{h}^{(t-1)}$共同得到。得到的$\boldsymbol{h}^{(t)}$方面用于当前层的模型损失计算，另一方面用于计算下一层的$\boldsymbol{h}^{(t+1)}$。

由于RNN梯度消失的问题，大牛们对于序列索引位置t的隐藏结构做了改进，可以说通过一些技巧让隐藏结构复杂了起来，来避免梯度消失的问题，这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种，这里我们以最常见的LSTM为例讲述。LSTM的结构如下图：

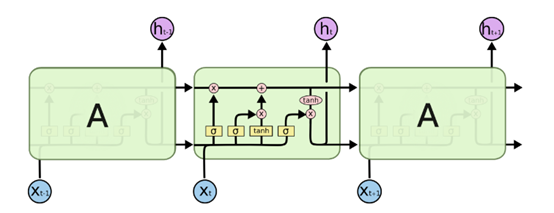
5.1.1 LSTM之细胞状态

上面我们给出了LSTM的模型结构，下面我们就一点点的剖析LSTM模型在每个序列索引位置$t$时刻的内部结构。

从上图中可以看出，在每个序列索引位置$t$时刻向前传播的除了和RNN一样的隐藏状态$\boldsymbol{h}^{(t+1)}$，还多了另一个隐藏状态，如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State)，记为$\boldsymbol{C}^{(t)}$。如下图所示：

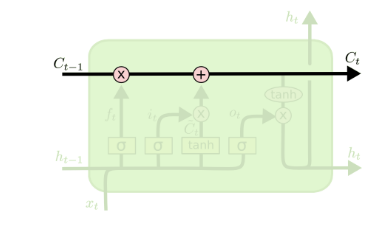
我们可以看到从$\boldsymbol{C}^{(t - 1)}$到$\boldsymbol{C}^{(t)}$，似乎经过了若干乘法和加法操作。

除了细胞状态，LSTM图中还有了很多奇怪的结构，这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门，输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门，输入门和输出门以及细胞状态。

5.1.2 LSTM之遗忘门

遗忘门（forget gate）顾名思义，是控制是否遗忘的，在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示：

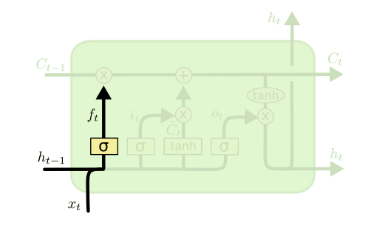
图中输入的有上一序列的隐藏状态$\boldsymbol{h}^{(t - 1)}$和$t$时刻的输入$\boldsymbol{x}^{(t)}$，通过一个激活函数（一般是sigmoid），得到遗忘门的输出$\boldsymbol{f}^{(t)}$：

$\boldsymbol{f}^{(t)} = \sigma\left( {\boldsymbol{W}_{f}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{f}\boldsymbol{x}^{(t)} + \boldsymbol{b}_{f}} \right)$

由于sigmoid的值域介于0~1之间，所以这里的$\boldsymbol{f}^{(t)}$表示保留上一个时间步$\boldsymbol{h}^{(t - 1)}$的多大的成分。虽然“保留”跟“遗忘门”这两个词是概念上相反的，但大家似乎已经习惯用遗忘门来称呼这个$\boldsymbol{f}^{(t)}$了。

5.1.3 LSTM之输入门

输入门（input gate）负责管理当前序列位置的输入，它的子结构如下图：

输入门$\boldsymbol{i}^{(t)}$的数学表达式为：

$\boldsymbol{i}^{(t)} = \sigma\left( {\boldsymbol{W}_{i}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{i}\boldsymbol{x}^{(t)} + \boldsymbol{b}_{i}} \right)$

对比遗忘门的表达式，除了矩阵的下标发生了点改变以外，其他都一样。

而遗忘门的控制对象则是$\boldsymbol{h}^{(t - 1)}$和$\boldsymbol{x}^{(t)}$组合的产物，它的表达式如下：

$\boldsymbol{a}^{(t)} = \sigma\left( {\boldsymbol{W}_{a}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{a}\boldsymbol{x}^{(t)} + \boldsymbol{b}_{a}} \right)$

5.1.4 LSTM之细胞状态更新

在研究LSTM输出门之前，我们要先看看LSTM的细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态$\boldsymbol{C}^{(t)}$。我们来看看$\boldsymbol{C}^{(t - 1)}$是如何得到$\boldsymbol{C}^{(t)}$的：

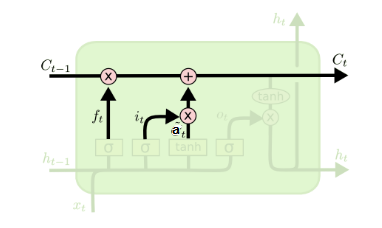
细胞状态$\boldsymbol{C}^{(t)}$由两部分组成，第一部分是$\boldsymbol{C}^{(t - 1)}$和遗忘门$\boldsymbol{f}^{(t)}$的Hadamard积（逐元素相乘），第二部分是$\boldsymbol{a}^{(t)}$和输入门$\boldsymbol{i}^{(t)}$的Hadamard积：

$\boldsymbol{C}^{(t)} = \boldsymbol{C}^{(t)}\bigodot\boldsymbol{f}^{(t)} + \boldsymbol{a}^{(t)}\bigodot\boldsymbol{i}^{(t)}$

5.1.5 LSTM之输出门

有了新的隐藏细胞状态$\boldsymbol{C}^{(t)}$，现在来到输出门：

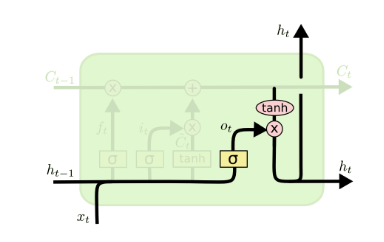
输出门$\boldsymbol{o}^{(t)}$的数学表达式为：

$\boldsymbol{o}^{(t)} = \sigma\left( {\boldsymbol{W}_{o}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{o}\boldsymbol{x}^{(t - 1)} + \boldsymbol{b}_{o}} \right)$

而输出门所控制的对象，则是$tanh\left( \boldsymbol{C}^{(t)} \right)$，两者共同形成$t$时间步下的隐藏状态$\boldsymbol{h}^{(t)}$：

$\boldsymbol{h}^{(t)} = \boldsymbol{o}^{(t)}\bigodot tanh\left( \boldsymbol{C}^{(t)} \right)$

5.1.6 LSTM前向传播总结

现在我们来总结下LSTM前向传播算法。LSTM模型有两个隐藏状态$\boldsymbol{h}^{(t)}$，$\boldsymbol{C}^{(t)}$，模型参数恰好是RNN的4倍整。

前向传播过程在每个时间步$t$上发生的顺序为：

1）更新遗忘门输出：

$\boldsymbol{f}^{(t)} = \sigma\left( {\boldsymbol{W}_{f}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{f}\boldsymbol{x}^{(t)} + \boldsymbol{b}_{f}} \right)$

2）更新输入门和其控制对象：

$\boldsymbol{i}^{(t)} = \sigma\left( {\boldsymbol{W}_{i}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{i}\boldsymbol{x}^{(t)} + \boldsymbol{b}_{i}} \right)$

$\boldsymbol{a}^{(t)} = tanh\left( {\boldsymbol{W}_{a}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{a}\boldsymbol{x}^{(t)} + \boldsymbol{b}_{a}} \right)$

3）更新细胞状态，从而$\left. \boldsymbol{C}^{(t - 1)}\longrightarrow\boldsymbol{C}^{(t)} \right.$：

$\boldsymbol{C}^{(t)} = \boldsymbol{C}^{(t - 1)}\bigodot\boldsymbol{f}^{(t)} + \boldsymbol{a}^{(t)}\bigodot\boldsymbol{i}^{(t)}$

4）更新输出门和其控制对象，从而$\left. \boldsymbol{h}^{(t - 1)}\longrightarrow\boldsymbol{h}^{(t)} \right.$：

$\boldsymbol{o}^{(t)} = \sigma\left( {\boldsymbol{W}_{o}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{o}\boldsymbol{x}^{(t - 1)} + \boldsymbol{b}_{o}} \right)$

$\boldsymbol{h}^{(t)} = \boldsymbol{o}^{(t)}\bigodot tanh\left( \boldsymbol{C}^{(t)} \right)$

5）得到当前时间步$t$的预测输出：

${\hat{\boldsymbol{y}}}^{(t)} = \sigma\left( {\boldsymbol{V}\boldsymbol{h}^{(t)} + \boldsymbol{c}} \right)$

5.2 LSTM的反向梯度推导

在RNN中，为了计算反向传播误差，我们通过隐藏状态$\boldsymbol{h}^{(t)}$的梯度$\boldsymbol{\delta}^{(t)}$一步一步向前传播。在LSTM中也类似，只不过我们这里由两种隐藏状态$\boldsymbol{h}^{(t)}$和$\boldsymbol{C}^{(t)}$，这里我们定义两种$\boldsymbol{\delta}$：

$\boldsymbol{\delta}_{h}^{(t)} = \frac{\partial L}{\partial\boldsymbol{h}^{(t)}}$

$\boldsymbol{\delta}_{C}^{(t)} = \frac{\partial L}{\partial\boldsymbol{C}^{(t)}}$

为了方便找到梯度的递推模式，下面是根据前向传播公式给出数据在LSTM中数据的前向流动示意图：

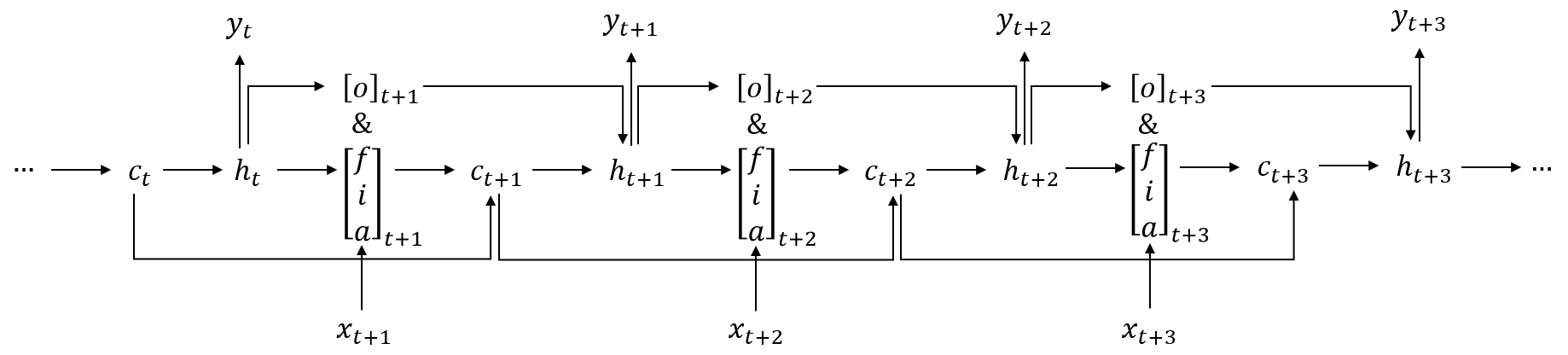
对于$t = T$，即时间序列截止的那个时间步，我们可以得到：

$\boldsymbol{\delta}_{h}^{(T)} = \boldsymbol{V}^{T}\left( {{\hat{\boldsymbol{y}}}^{(T)} - \boldsymbol{y}^{(T)}} \right)$

$\boldsymbol{\delta}_{C}^{(T)} = \left( \frac{\partial\boldsymbol{h}^{(T)}}{\partial\boldsymbol{C}^{(T)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(T)}} = \boldsymbol{\delta}_{h}^{(T)}\bigodot\boldsymbol{o}^{(T)}\bigodot{tanh}^{'}\left( \boldsymbol{C}^{(T)} \right)$

第一个式子的证明见vanilla RNN的前向传播和反向梯度推导的4.2节；第二个式子根据等式$\boldsymbol{h}^{(t)} = \boldsymbol{o}^{(t)}\bigodot tanh\left( \boldsymbol{C}^{(t)} \right)$结合数学基础篇：矩阵微分与求导的理论即可秒证出来。

对于$t < T$时，我们要利用$\boldsymbol{\delta}_{h}^{(t + 1)}$和$\boldsymbol{\delta}_{C}^{(t + 1)}$递推得到$\boldsymbol{\delta}_{h}^{(t)}$和$\boldsymbol{\delta}_{C}^{(t)}$。

先来推导$\boldsymbol{\delta}_{h}^{(t)}$的递推公式：

根据上图我们知道，$\boldsymbol{\delta}_{h}^{(t)}$的误差来源如下：

1）$\left. l\left( t \right)\longrightarrow\boldsymbol{h}^{(t)} \right.$

2）$\left. \boldsymbol{h}^{(t + 1)}\longrightarrow\boldsymbol{o}^{(t + 1)}\longrightarrow\boldsymbol{h}^{(t)} \right.$

3）$\left. \boldsymbol{C}^{(t + 1)}\longrightarrow\boldsymbol{i}^{(t + 1)}\longrightarrow\boldsymbol{h}^{(t)} \right.$

4）$\left. \boldsymbol{C}^{(t + 1)}\longrightarrow\boldsymbol{a}^{(t + 1)}\longrightarrow\boldsymbol{h}^{(t)} \right.$

5）$\left. \boldsymbol{C}^{(t + 1)}\longrightarrow\boldsymbol{f}^{(t + 1)}\longrightarrow\boldsymbol{h}^{(t)} \right.$

根据链式法则和全微分方程，有：

$\boldsymbol{\delta}_{h}^{(t)} = \frac{\partial L\left( t \right)}{\partial\boldsymbol{h}^{(t)}} = \frac{\partial l\left( t \right)}{\partial\boldsymbol{h}^{(t)}} + \left( \frac{\partial\boldsymbol{C}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} \right)^{T}\boldsymbol{\delta}_{C}^{(t + 1)} + \left( {\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{o}^{(t + 1)}}\frac{\partial\boldsymbol{o}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}} \right)^{T}\boldsymbol{\delta}_{h}^{(t + 1)}$

注意：上式中特地用了$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{o}^{(t + 1)}}\frac{\partial\boldsymbol{o}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$而不是$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$。因为在$\boldsymbol{h}^{(t + 1)}$与$\boldsymbol{h}^{(t)}$之间存在多条传播路径的情况下，$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{o}^{(t + 1)}}\frac{\partial\boldsymbol{o}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} \neq \frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$。我们用$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{o}^{(t + 1)}}\frac{\partial\boldsymbol{o}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$规定了从$\boldsymbol{h}^{(t + 1)}$到$\boldsymbol{h}^{(t)}$的误差传播路径必须是$\left. \boldsymbol{h}^{(t + 1)}\longrightarrow\boldsymbol{o}^{(t + 1)}\longrightarrow\boldsymbol{h}^{(t)} \right.$而不是其他的路径。如果是用$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$这个符号，则是默认要考虑所有从$\boldsymbol{h}^{(t + 1)}$到$\boldsymbol{h}^{(t)}$的误差传播路径。

上面这个递推公式需要解决三个问题，$\frac{\partial l\left( t \right)}{\partial\boldsymbol{h}^{(t)}}$，$\left( \frac{\partial\boldsymbol{C}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} \right)^{T}$和$\left( {\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{o}^{(t + 1)}}\frac{\partial\boldsymbol{o}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}} \right)^{T}$的求解。

对于$\frac{\partial l\left( t \right)}{\partial\boldsymbol{h}^{(t)}}$，根据vanilla RNN的前向传播和反向梯度推导的4.2节，它满足：

$\frac{\partial l\left( t \right)}{\partial\boldsymbol{h}^{(t)}} = \boldsymbol{V}^{T}\left( {{\hat{\boldsymbol{y}}}^{(t)} - \boldsymbol{y}^{(t)}} \right)$

我们接下来求$\frac{\partial\boldsymbol{C}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$：

注意：因为下面的公式实在太长了，所以为节省空间，我们用“~”表示这个位置原本的数学表达式与上一行相同位置的数学表达式一样。

基于$\boldsymbol{C}^{(t)} = \boldsymbol{C}^{(t - 1)}\bigodot\boldsymbol{f}^{(t)} + \boldsymbol{a}^{(t)}\bigodot\boldsymbol{i}^{(t)}$逐层展开，我们得到：

$d\boldsymbol{C}^{(t + 1)} = \boldsymbol{C}^{(t)}\bigodot d\boldsymbol{f}^{({t + 1})} + \boldsymbol{i}^{({t + 1})}\bigodot d\boldsymbol{a}^{({t + 1})} + \boldsymbol{a}^{({t + 1})}\bigodot d\boldsymbol{i}^{({t + 1})}$

$= diag\left( \boldsymbol{C}^{(t)} \right)d\boldsymbol{f}^{({t + 1})} + diag\left( \boldsymbol{i}^{({t + 1})} \right)d\boldsymbol{a}^{({t + 1})} + diag\left( \boldsymbol{a}^{({t + 1})} \right)d\boldsymbol{i}^{({t + 1})}$

$= diag\left( \boldsymbol{C}^{(t)} \right)d\boldsymbol{f}^{({t + 1})} + diag\left( \boldsymbol{a}^{({t + 1})} \right)d\boldsymbol{i}^{({t + 1})} + diag\left( \boldsymbol{i}^{({t + 1})} \right)d\boldsymbol{a}^{({t + 1})}$

$\left. = diag\left( {\boldsymbol{C}^{(t)}\bigodot\boldsymbol{f}^{({t + 1})}\bigodot\left( {1 - \boldsymbol{f}^{({t + 1})}} \right)} \right)\boldsymbol{W}_{f}d\boldsymbol{h}^{(t)} + \right.\sim\left. + \right.\sim$

$\left. = \right.\sim\left. + diag\left( {\boldsymbol{a}^{({t + 1})}\bigodot\boldsymbol{i}^{({t + 1})}\bigodot\left( {1 - \boldsymbol{i}^{({t + 1})}} \right)} \right)\boldsymbol{W}_{i}d\boldsymbol{h}^{(t)} + \right.\sim$

因为${tanh}^{'}\left( x \right) = \left( {1 - {tanh\left( x \right)}^{2}} \right)$，所以：

$\left. d\boldsymbol{C}^{(t + 1)} = \right.\sim\left. + \right.\sim + diag\left( {\boldsymbol{i}^{({t + 1})}\bigodot\left( {1 - {\boldsymbol{a}^{({t + 1})}}^{2}} \right)} \right)\boldsymbol{W}_{a}d\boldsymbol{h}^{(t)}$

整理上式我们得到：

$\frac{\partial\boldsymbol{C}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} = diag\left( {\boldsymbol{C}^{(t)}\bigodot\boldsymbol{f}^{({t + 1})}\bigodot\left( {1 - \boldsymbol{f}^{({t + 1})}} \right)} \right)\boldsymbol{W}_{f} + diag\left( {\boldsymbol{a}^{({t + 1})}\bigodot\boldsymbol{i}^{({t + 1})}\bigodot\left( {1 - \boldsymbol{i}^{({t + 1})}} \right)} \right)\boldsymbol{W}_{i} + diag\left( {\boldsymbol{i}^{({t + 1})}\bigodot\left( {1 - {\boldsymbol{a}^{({t + 1})}}^{2}} \right)} \right)\boldsymbol{W}_{a}$

接下来是$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{o}^{(t + 1)}}\frac{\partial\boldsymbol{o}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$的推导过程：

$d\boldsymbol{h}^{({t + 1})} = tanh\left( \boldsymbol{C}^{({t + 1})} \right)\bigodot d\boldsymbol{o}^{({t + 1})} = diag\left( {tanh\left( \boldsymbol{C}^{({t + 1})} \right)} \right)diag\left( {\boldsymbol{o}^{({t + 1})}\bigodot\left( {1 - \boldsymbol{o}^{({t + 1})}} \right)} \right)d\left( {\boldsymbol{W}_{o}\boldsymbol{h}^{(t)}} \right) = diag\left( {tanh\left( \boldsymbol{C}^{({t + 1})} \right)\bigodot\boldsymbol{o}^{({t + 1})}\bigodot\left( {1 - \boldsymbol{o}^{({t + 1})}} \right)} \right)\boldsymbol{W}_{o}d\boldsymbol{h}^{(t)}$

所以$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{o}^{(t + 1)}}\frac{\partial\boldsymbol{o}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} = diag\left( {tanh\left( \boldsymbol{C}^{({t + 1})} \right)\bigodot\boldsymbol{o}^{({t + 1})}\bigodot\left( {1 - \boldsymbol{o}^{({t + 1})}} \right)} \right)$

于是我们现在得到了从$\boldsymbol{\delta}_{C}^{(t + 1)}$和$\boldsymbol{\delta}_{h}^{(t + 1)}$推得$\boldsymbol{\delta}_{h}^{(t)}$的递推公式。

接下来我们利用$\boldsymbol{\delta}_{h}^{(t)}$和$\boldsymbol{\delta}_{C}^{(t + 1)}$来推得$\boldsymbol{\delta}_{C}^{(t)}$：

根据LSTM的前向示意图，我们有：

容易求得$\frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{c}^{(t)}} = \left( \frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{C}^{(t)}} \right)^{T}\frac{\partial L\left( t \right)}{\partial\boldsymbol{h}^{(t)}} = \boldsymbol{o}^{(t)} \odot \left( {1 - {tanh}^{2}\left( \boldsymbol{C}^{(t)} \right)} \right)^{2}$

同样也容易求得$\frac{\partial\boldsymbol{c}^{(t + 1)}}{\partial\boldsymbol{c}^{(t)}} = diag\left( \boldsymbol{f}^{({t + 1})} \right)$

所以得到：

$\boldsymbol{\delta}_{C}^{(t)} = \left( \frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{c}^{(t)}} \right)^{T}\boldsymbol{\delta}_{h}^{(t)} + {\left( \frac{\partial\boldsymbol{c}^{(t + 1)}}{\partial\boldsymbol{c}^{(t)}} \right)^{T}\boldsymbol{\delta}}_{C}^{(t + 1)} = \boldsymbol{o}^{(t)} \odot \left( {1 - {tanh}^{2}\left( \boldsymbol{C}^{(t)} \right)} \right)^{2}{\odot \boldsymbol{\delta}}_{h}^{(t)} + \boldsymbol{f}^{({t + 1})} \odot \boldsymbol{\delta}_{C}^{(t + 1)}$

现在，我们能计算$\boldsymbol{\delta}_{h}^{(t)}$和$\boldsymbol{\delta}_{C}^{(t)}$了，有了它们，计算变量的梯度就比较容易了，这里只以计算$\boldsymbol{W}_{f}$的梯度计算为例：

我们令${\boldsymbol{z}^{(t)} = \boldsymbol{W}}_{f}\boldsymbol{h}^{(t - 1)} + \boldsymbol{U}_{f}\boldsymbol{x}^{(t)} + \boldsymbol{b}_{f}$，则：

$\frac{\partial L}{\partial\boldsymbol{W}_{f}} = {\sum\limits_{t = 1}^{T}\left( \frac{\partial\boldsymbol{C}_{t}}{\partial\boldsymbol{z}^{(t)}} \right)^{T}}\frac{\partial L}{\partial\boldsymbol{C}_{t}}\left( \boldsymbol{h}^{(t - 1)} \right)^{T}$

$d\boldsymbol{C}^{(t)} = \boldsymbol{C}^{(t - 1)} \odot d\boldsymbol{f}^{(t)} = diag\left( \boldsymbol{C}^{({t - 1})} \right)\left( {\left( {\boldsymbol{f}^{(t)} \odot \left( {1 - \boldsymbol{f}^{(t)}} \right)} \right) \odot d\boldsymbol{z}^{(t)}} \right) = diag\left( \boldsymbol{C}^{({t - 1})} \right)\left( {diag\left( {\boldsymbol{f}^{(t)} \odot \left( {1 - \boldsymbol{f}^{(t)}} \right)} \right)d\boldsymbol{z}^{(t)}} \right) = diag\left( {\boldsymbol{f}^{(t)} \odot \left( {1 - \boldsymbol{f}^{(t)}} \right) \odot \boldsymbol{C}^{({t - 1})}} \right)d\boldsymbol{z}^{(t)}$

所以$\frac{\partial\boldsymbol{C}_{t}}{\partial\boldsymbol{z}^{(t)}} = diag\left( {\boldsymbol{f}^{(t)} \odot \left( {1 - \boldsymbol{f}^{(t)}} \right) \odot \boldsymbol{C}^{({t - 1})}} \right)$

所以得到：

$\frac{\partial L}{\partial\boldsymbol{W}_{f}} = {\sum\limits_{t = 1}^{T}\left\lbrack {\boldsymbol{\delta}_{C}^{(t)} \odot \boldsymbol{C}^{(t - 1)} \odot \boldsymbol{f}^{(t)} \odot \left\lbrack {1 - \boldsymbol{f}^{(t)}} \right\rbrack} \right\rbrack}\left( \boldsymbol{h}^{(t - 1)} \right)^{T}$

其他变量的梯度按照上述类似的方式可依次求得，在这里不做过多叙述。

5.3 LSTM 能改善梯度消失的原因

首先需要明确的是，RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。MLP/CNN 中不同的层有不同的参数，各是各的梯度；而 RNN 中同样的权重在各个时间步共享，最终的梯度$~g$= 各个时间步的梯度$g^{(t)}$之和。

因此，RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。

LSTM 中梯度的传播有很多条路径，但$\boldsymbol{C}^{(t)} = \boldsymbol{C}^{(t - 1)}\bigodot\boldsymbol{f}^{(t)} + \boldsymbol{a}^{(t)}\bigodot\boldsymbol{i}^{(t)}$这条路径上只有逐元素相乘和相加的操作，梯度流最稳定；但是其他路径上梯度流与普通 RNN 类似，照样会发生相同的权重矩阵反复连乘。

由于总的远距离梯度 = 各条路径的远距离梯度之和，即便其他远距离路径梯度消失了，只要保证有一条远距离路径（就是上面说的那条高速公路）梯度不消失，总的远距离梯度就不会消失（正常梯度 + 消失梯度 = 正常梯度）。因此 LSTM 通过改善一条路径上的梯度问题拯救了总体的远距离梯度。

如果本文对您有所帮助的话，不妨点下“推荐”让它能帮到更多的人，谢谢。

参考资料

（欢迎转载，转载请注明出处。欢迎留言或沟通交流： lxwalyw@gmail.com）

posted @ 2020-09-07 09:23 SumwaiLiu 阅读(1714) 评论(5) 编辑收藏举报

刷新页面返回顶部

一唯绛