《神经网络的梯度推导与代码验证》之FNN(DNN)的前向传播和反向梯度推导
在《神经网络的梯度推导与代码验证》之数学基础篇:矩阵微分与求导中,我们总结了一些用于推导神经网络反向梯度求导的重要的数学技巧。此外,通过一个简单的demo,我们初步了解了使用矩阵求导来批量求神经网络参数的做法。在本篇章,我们将专门针对DNN/FNN这种网络结构进行前向传播介绍和反向梯度推导。更多相关内容请见《神经网络的梯度推导与代码验证》系列介绍。
注意:
- 本系列的关注点主要在反向梯度推导以及代码上的验证,涉及到的前向传播相对而言不会做太详细的介绍。
- 反向梯度求导涉及到矩阵微分和求导的相关知识,请见《神经网络的梯度推导与代码验证》之数学基础篇:矩阵微分与求导,内含手把手教学级的内容。
目录
- 2.1 FNN(DNN)的前向传播
- 2.2 FNN(DNN)的反向传播
- 2.3 总结
- 参考资料
提醒:
- 后续会反复出现$\boldsymbol{\delta}^{l}$这个(类)符号,它的定义为$\boldsymbol{\delta}^{l} = \frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l}}}$,即loss $l$对$\boldsymbol{z}^{\boldsymbol{l}}$的导数
- 其中$\boldsymbol{z}^{\boldsymbol{l}}$表示第$l$层(DNN,CNN,RNN或其他例如max pooling层等)未经过激活函数的输出。
- $\boldsymbol{a}^{\boldsymbol{l}}$则表示$\boldsymbol{z}^{\boldsymbol{l}}$经过激活函数后的输出。
这些符号会贯穿整个系列,还请留意。
2.1 FNN(DNN)的前向传播
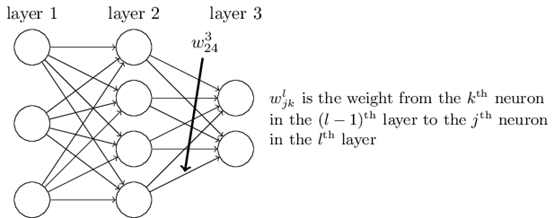
下面是两张DNN的示意图:
我们用$w_{24}^{3}$来表示第2层的第4个神经元与第三层第2个神经元之间的参数。
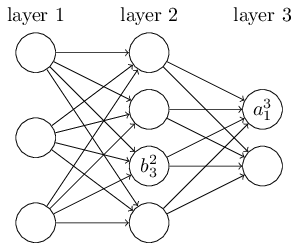
我们用$b_{3}^{2}$表示第2层的第3个神经元的偏置。用$a_{1}^{3}$表示第3层的第1个神经元的输出(注意是经过激活函数后的)。
上图的从第一层到第二层的参数计算公式如下:
$a_{1}^{2} = \sigma\left( {w_{11}^{2}x_{1} + w_{12}^{2}x_{2} + w_{13}^{2}x_{3} + b_{1}^{2}} \right)$
$a_{2}^{2} = \sigma\left( {w_{21}^{2}x_{1} + w_{22}^{2}x_{2} + w_{23}^{2}x_{3} + b_{2}^{2}} \right)$
$a_{3}^{2} = \sigma\left( {w_{31}^{2}x_{1} + w_{32}^{2}x_{2} + w_{33}^{2}x_{3} + b_{3}^{2}} \right)$
$a_{4}^{2} = \sigma\left( {w_{41}^{2}x_{1} + w_{42}^{2}x_{2} + w_{43}^{2}x_{3} + b_{4}^{2}} \right)$
其中$\sigma\left( ~ \right)$表示激活函数。
将上图写成矩阵的编排方式就是下面这样:
$\left\lbrack \begin{array}{l} \begin{array}{l} a_{1}^{2} \\ a_{2}^{2} \\ \end{array} \\ a_{3}^{2} \\ a_{4}^{2} \\ \end{array} \right\rbrack = \sigma\left( {\left\lbrack \begin{array}{lll} \begin{array}{l} w_{11}^{2} \\ w_{21}^{2} \\ \end{array} & \begin{array}{l} w_{12}^{2} \\ w_{22}^{2} \\ \end{array} & \begin{array}{l} w_{13}^{2} \\ w_{23}^{2} \\ \end{array} \\ w_{31}^{2} & w_{32}^{2} & w_{33}^{2} \\ w_{41}^{2} & w_{42}^{2} & w_{43}^{2} \\ \end{array} \right\rbrack\left\lbrack \begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \\ \end{array} \right\rbrack + \left\lbrack \begin{array}{l} \begin{array}{l} b_{1}^{2} \\ b_{2}^{2} \\ \end{array} \\ b_{3}^{2} \\ b_{4}^{2} \\ \end{array} \right\rbrack} \right)$
即
$\boldsymbol{a}^{2} = \sigma\left( {\boldsymbol{W}^{2}\boldsymbol{x} + \boldsymbol{b}^{2}} \right)$
同理得到第二层到第三层的计算公式:
$\boldsymbol{a}^{3} = \sigma\left( {\boldsymbol{W}^{3}\boldsymbol{a}^{2} + \boldsymbol{b}^{3}} \right)$
于是总结下来,DNN的层间关系如下:
$\boldsymbol{a}^{\boldsymbol{l}} = \sigma\left( {\boldsymbol{W}^{l}\boldsymbol{a}^{l - 1} + \boldsymbol{b}^{l}} \right)$
所以DNN的前向传播逻辑如下:
输入:总层数L,所有隐藏层和输出层对应的参数矩阵$\boldsymbol{W}$,偏置向量$\boldsymbol{b}$和输入向量$\boldsymbol{x}$
输出:$\boldsymbol{a}^{L}$
1) 初始化$\boldsymbol{a}^{1} = \boldsymbol{x}$
2) for $l = 2$ to L,计算:$\boldsymbol{a}^{l} = \sigma\left( {\boldsymbol{W}^{l}\boldsymbol{a}^{l - 1} + \boldsymbol{b}^{l}} \right)$
最后的结果即为输出$\boldsymbol{a}^{L}$
2.2 FNN(DNN)的反向梯度求导
在进行DNN反向传播算法前,我们需要选择一个损失函数,来度量训练样本计算出的输出和真实的训练样本输出之间的损失。这里用mse作为损失函数,则每一条样本的loss计算公式如下:
$l = \frac{1}{2}\left\| {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right\|_{2}^{2} = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)$
其中,$\boldsymbol{y}$就是样本标签$\boldsymbol{y}\_\boldsymbol{t}\boldsymbol{u}\boldsymbol{r}\boldsymbol{e}$,而$\boldsymbol{a}^{\boldsymbol{L}}$就是预测值$\boldsymbol{y}\_\boldsymbol{p}\boldsymbol{r}\boldsymbol{e}\boldsymbol{d}\boldsymbol{i}\boldsymbol{c}\boldsymbol{t}$。
预测值$\boldsymbol{a}^{\boldsymbol{L}}$和输入$\boldsymbol{x}$满足$\boldsymbol{a}^{\boldsymbol{L}} = \boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left( {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right)$,这就是2.1中提到的DNN的前向传播过程,这么看来,所谓前向传播,不过是一个复杂的函数罢了。
于是写得再全一点,某条样本$\boldsymbol{a}^{\boldsymbol{L}} = \boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left( {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right)$根据mse计算出来的loss就是下面这样:
$l\left( {\boldsymbol{x},\boldsymbol{y},\boldsymbol{W},\boldsymbol{b}} \right) = \frac{1}{2}\left\| {\boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left\| {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right\| - \boldsymbol{y}} \right\|_{2}^{2} = \frac{1}{2}\left( {\boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left( {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right) - \boldsymbol{y}} \right)^{T}\left( {\boldsymbol{D}\boldsymbol{N}\boldsymbol{N}\left( {\boldsymbol{x};\boldsymbol{W},\boldsymbol{b}} \right) - \boldsymbol{y}} \right)$
铺垫了这么多接下来正式开始求梯度。
我们先求$\frac{\partial l}{\partial\boldsymbol{a}^{\boldsymbol{L}}}$,
$dl = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T}d\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) + \frac{1}{2}d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T}d\boldsymbol{a}^{\boldsymbol{L}} + \frac{1}{2}d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)$
对$\frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)$使用迹技巧,有:
$\frac{1}{2}d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) = \frac{1}{2}tr\left( {d\left( \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)} \right) = \frac{1}{2}tr\left( {\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)} \right) = \frac{1}{2}tr\left( {\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\boldsymbol{a}^{\boldsymbol{L}}} \right) = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\boldsymbol{a}^{\boldsymbol{L}}$
所以有:
$dl = \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{T}d\boldsymbol{a}^{\boldsymbol{L}} + \frac{1}{2}\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\boldsymbol{a}^{\boldsymbol{L}} = \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right)^{\boldsymbol{T}}d\boldsymbol{a}^{\boldsymbol{L}}$
$\frac{\partial l}{\partial\boldsymbol{a}^{\boldsymbol{L}}} = \boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}$
我们令$\boldsymbol{z}^{L} = \boldsymbol{W}^{\boldsymbol{L}}\boldsymbol{a}^{\boldsymbol{L} - 1} + \boldsymbol{b}^{\boldsymbol{L}}$
可求得$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}} = \left( \frac{\partial\boldsymbol{a}^{\boldsymbol{L}}}{\partial\boldsymbol{a}^{\boldsymbol{L}}} \right)^{T}\frac{\partial l}{\partial\boldsymbol{a}^{\boldsymbol{L}}}$
因为$d\boldsymbol{a}^{\boldsymbol{L}} = d\sigma\left( \boldsymbol{z}^{L} \right) = \sigma^{'}\left( \boldsymbol{z}^{L} \right) \odot d\boldsymbol{z}^{L} = diag\left( {\sigma^{'}\left( \boldsymbol{z}^{L} \right)} \right)d\boldsymbol{z}^{L}$
所以$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}} = diag\left( {\sigma^{'}\left( \boldsymbol{z}^{L} \right)} \right)\left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) = \left( {\boldsymbol{a}^{\boldsymbol{L}} - \boldsymbol{y}} \right) \odot \sigma^{'}\left( \boldsymbol{z}^{L} \right)$
有了$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}}$,那么求L层的$\boldsymbol{W}^{\boldsymbol{L}}$和$\boldsymbol{b}^{\boldsymbol{L}}$的梯度就非常容易了,根据标量对线性变换的求导结论,直接得到:
$\frac{\partial l}{\partial\boldsymbol{W}^{\boldsymbol{L}}} = \frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}}\left( \boldsymbol{a}^{\boldsymbol{L} - 1} \right)^{T}$
$\frac{\partial l}{\partial\boldsymbol{b}^{\boldsymbol{L}}} = \frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{L}}}$
这样第L层的所有参数的梯度就得到了。
为了方便起见,今后用$\delta^{l}$表示$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l}}}$。
有上面求L层参数的梯度的思路,可以发现,如果我们想求出第$l$层的参数的梯度,我们可以先求出$\delta^{l}$然后直接套用标量对线性变换的求导结论就可以快速求得结果了。因此,这里我们用数学归纳法,第L层的$\delta^{L}$我们已经求出来了,假设第$l+1$层的$\delta^{l + 1}$已求出来,那我们如何求$\delta^{l}$呢?
根据链式法则,有$\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l}}} = \left( \frac{\partial\boldsymbol{z}^{\boldsymbol{l} + 1}}{\partial\boldsymbol{z}^{\boldsymbol{l}}} \right)^{T}\frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l} + 1}}$
现在问题转到求$\frac{\partial\boldsymbol{z}^{\boldsymbol{l} + 1}}{\partial\boldsymbol{z}^{\boldsymbol{l}}}$上。
我们注意到有$\boldsymbol{z}^{l + 1} = \boldsymbol{W}^{l + 1}\sigma\left( \boldsymbol{z}^{\boldsymbol{l}} \right) + \boldsymbol{b}^{l + 1}$成立,
所以$d\boldsymbol{z}^{l + 1} = \boldsymbol{W}^{l + 1}d\sigma\left( \boldsymbol{z}^{\boldsymbol{l}} \right) = \boldsymbol{W}^{l + 1}\left( {\sigma^{'}\left( \boldsymbol{z}^{l} \right) \odot d\boldsymbol{z}^{l}} \right) = \boldsymbol{W}^{l + 1}diag\left( {\sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)} \right)d\boldsymbol{z}^{\boldsymbol{l}}$
所以$\frac{\partial\boldsymbol{z}^{l + 1}}{\partial\boldsymbol{z}^{l}} = \boldsymbol{W}^{l + 1}diag\left( {\sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)} \right)$
于是通过$\delta^{l + 1}$,我们可以求得:
$\delta^{l} = diag\left( {\sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)} \right)\left( \boldsymbol{W}^{l + 1} \right)^{T}\delta^{l + 1} = \left( \boldsymbol{W}^{l + 1} \right)^{T}\delta^{l + 1} \odot \sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)$
同理,根据$\delta^{l + 1}$可以秒求出$\boldsymbol{W}^{l} = \delta^{l}\left( \boldsymbol{a}^{\boldsymbol{l} - 1} \right)^{T}$,$\boldsymbol{b}^{\boldsymbol{l}} = \delta^{l}$
2.3 总结
在求神经网络某一层的参数的梯度时,先求出$\delta^{l}$是一种比较合理的策略,因为借助标量对线性变换的求导结论可以快速通过$\delta^{l}$求得参数的梯度;通过推导出$\delta^{l}$与$\delta^{l+1}$的关系,可以将这种求参数梯度的模式推广到其他层上。
同时我们也可以发现,对参数梯度造成影响的因素主要有以下几个:
- 损失函数的选取,它决定了最初的$\frac{\partial l}{\partial\boldsymbol{a}^{\boldsymbol{L}}}$
- 激活函数的选取,它决定了层间$\delta^{l} = \boldsymbol{W}^{\boldsymbol{l} + 1}diag\left( {\sigma^{'}\left( \boldsymbol{z}^{\boldsymbol{l}} \right)} \right)\delta^{l + 1}$的递推计算
- 神经网络的参数,例如每一层的神经元个数影响了$\boldsymbol{W}$的尺寸;而整体深度则影响了神经网络隐藏层(尤其是靠前的隐藏层)的梯度稳定性(靠前的隐藏层可能会发生梯度消失或梯度爆炸)。
- 神经网络的结构,因为显然它会直接影响反向梯度的推导方式(在LSTM的反向梯度推导中大家会有更深的体会)。
如果本文对您有所帮助的话,不妨点下“推荐”让它能帮到更多的人,谢谢。
参考资料
- https://www.cnblogs.com/pinard/p/6418668.html
- https://www.cnblogs.com/pinard/p/6422831.html
(欢迎转载,转载请注明出处。欢迎留言或沟通交流: lxwalyw@gmail.com)