HDU 2084 数塔 简单动态规划

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2084

题目大意：
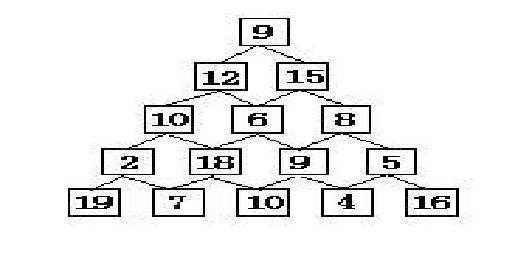
有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

题目分析：
首先我们可以给数塔中的每一个点制定一个坐标。
最上面的9的坐标是(1,1)，第二行的12的坐标是(2,1)，15的坐标是(2,2)，以此类推，第i行的第j个数的坐标就是(i,j)。
我们假设一共有n行，并且设a[i][j]为坐标为(i,j)对应的数，f[i][j]为从(i,j)点走到最底层所经过的节点的数字之和的最大值。
可以得出状态转移方程如下：
对于第N行的节点(n,j)来说，f[n][j] = a[n][j]
对于其他行的节点(i,j)来说，f[i][j] = max(f[i+1][j], f[i+1][j+1]) + a[i][j]
C++代码如下：

#include <cstdio>
#include <iostream>
using namespace std;
int T, n, a[110][110], f[110][110];
int main()
{
    scanf("%d", &T);
    while (T--)
    {
        scanf("%d", &n);
        for (int i = 1; i <= n; i ++)
            for (int j = 1; j <= i; j ++)
                scanf("%d", &a[i][j]);
        for (int i = 1; i <= n; i ++)
            f[n][i] = a[n][i];
        for (int i = n-1; i >= 1; i--)
            for (int j = 1; j <= i; j ++)
                f[i][j] = max(f[i+1][j], f[i+1][j+1]) + a[i][j];
        printf("%d\n", f[1][1]);
    }
    return 0;
}