线性回归、逻辑回归

线性回归

（1）目标

　　预测函数：

　　　　

　　即 

　　学得w和b后，模型就可以确定。

（2）一维情形

　　先假设输入特征只有一维。

　　，

　　使用均方差当做损失函数，最小化均方差，也就是最小二乘法。

　　　　　

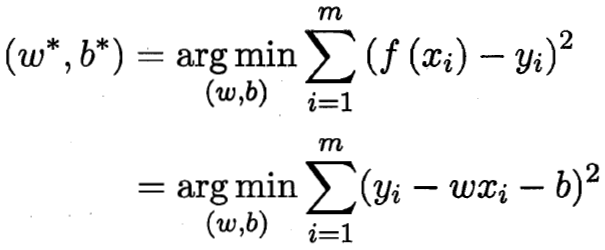
 　  求最小化均方差时的w和b，分别对上式w和b求导，使导数为0，即得到所求w*和b*。

　　　　

　　　　

　　

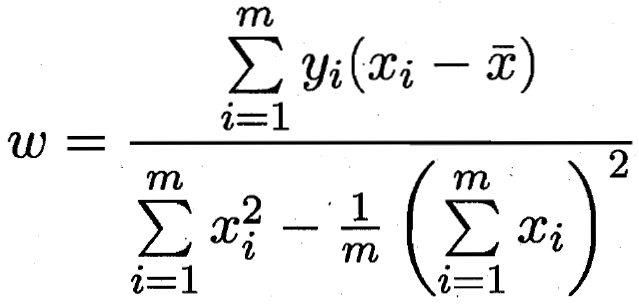
（3）推广到多维

　　现在考虑多维特征。

　　　　

　　把数据集D表示为一个矩阵X：

　　　　

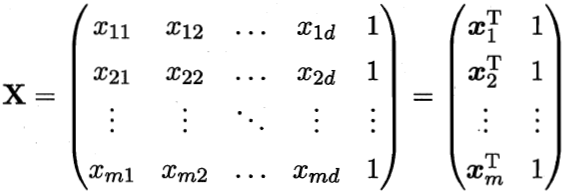
 　　此时，使用最小二乘法：

　　　　

　　令导数为0，解得：

　　实际计算中求以上矩阵计算量很大，因此常使用梯度下降法。二维情况下，函数变换最快的方向是斜率方向，多维情况下偏导就成为梯度，每次往负梯度方向走一步。

　　　　

 

逻辑回归

　　逻辑回归用于分类，在线性回归的基础上使用一个函数使得预测值与标记值联系起来。该函数需要连续可微，一般使用sigmoid函数。

　　　　

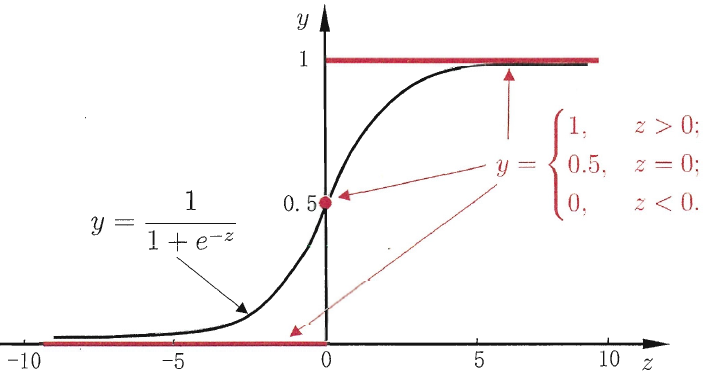
　　损失函数方面，线性回归的损失函数为平方损失函数，如果将其用于逻辑回归的损失函数，后续讨论的优化问题会变成非凸的，难以用梯度下降法求最优。因此逻辑回归使用负对数似然函数（交叉熵），它表示两个概率模型之间的相似度。

 　　　　

　　这个损失函数使用极大似然法得到。似然函数是在参数θ条件下，出现数据X的概率。极大似然法最大化这个概率，也就是最大化似然函数：L=P(X=x|θ)。

　　对于逻辑回归中参数w，似然函数：

　　　　

　　其中，f(x)最后加上了sigmoid，所以就是代表概率，因此：

　　　　        

　　所以 

　　代入 L(w) 得：

　　　　

　　对 L(w) 取对数得到对数似然函数（是因为(0,1)的小数连乘容易下溢导致结果为0）：

 　　　　

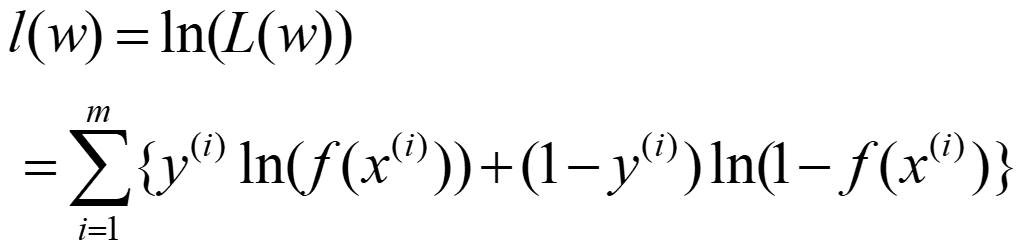
　　我们要最大化 l(w)，相当于最小化负 l(w)，即它的损失函数。

　　这个损失函数是高阶可导连续的凸函数，根据凸优化理论可以通过梯度下降法、牛顿法等方法求得最优解。