KNN邻近分类算法

K邻近（k-Nearest Neighbor，KNN）分类算法是最简单的机器学习算法了。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单：计算一个点A与其他所有点之间的距离，取出与该点最近的k个点，然后统计这k个点里面所属分类比例最大的，则点A属于该分类。

下面用一个例子来说明一下：

 

电影名称	打斗次数	接吻次数	电影类型
California Man	3	104	Romance
He’s Not Really into Dudes	2	100	Romance
Beautiful Woman	1	81	Romance
Kevin Longblade	101	10	Action
Robo Slayer 3000	99	5	Action
Amped II	98	2	Action

简单说一下这个数据的意思：这里用打斗次数和接吻次数来界定电影类型，如上，接吻多的是Romance类型的，而打斗多的是动作电影。还有一部名字未知（这里名字未知是为了防止能从名字中猜出电影类型），打斗次数为18次，接吻次数为90次的电影，它到底属于哪种类型的电影呢？

KNN算法要做的，就是先用打斗次数和接吻次数作为电影的坐标，然后计算其他六部电影与未知电影之间的距离，取得前K个距离最近的电影，然后统计这k个距离最近的电影里，属于哪种类型的电影最多，比如Action最多，则说明未知的这部电影属于动作片类型。

在实际使用中，有几个问题是值得注意的：K值的选取，选多大合适呢？计算两者间距离，用哪种距离会更好呢？计算量太大怎么办？假设样本中，类型分布非常不均，比如Action的电影有200部，但是Romance的电影只有20部，这样计算起来，即使不是Action的电影，也会因为Action的样本太多，导致k个最近邻居里有不少Action的电影，这样该怎么办呢？

没有万能的算法，只有在一定使用环境中最优的算法。

1.1 算法指导思想

kNN算法的指导思想是“近朱者赤，近墨者黑”，由你的邻居来推断出你的类别。

先计算待分类样本与已知类别的训练样本之间的距离，找到距离与待分类样本数据最近的k个邻居；再根据这些邻居所属的类别来判断待分类样本数据的类别。

 

1.2相似性度量

用空间内两个点的距离来度量。距离越大，表示两个点越不相似。距离的选择有很多^[13]，通常用比较简单的欧式距离。

欧式距离：

 

马氏距离：马氏距离能够缓解由于属性的线性组合带来的距离失真，是数据的协方差矩阵。

 

曼哈顿距离：

 

切比雪夫距离：

 

闵氏距离：r取值为2时：曼哈顿距离；r取值为1时：欧式距离。

 

 

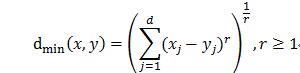
平均距离：

 

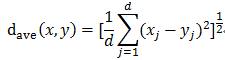
弦距离：

 

测地距离：

 

 

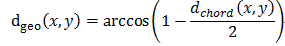
1.2 类别的判定

投票决定：少数服从多数，近邻中哪个类别的点最多就分为该类。

加权投票法：根据距离的远近，对近邻的投票进行加权，距离越近则权重越大（权重为距离平方的倒数）

 优缺点

1.2.1              优点

1. 简单，易于理解，易于实现，无需估计参数，无需训练；
2. 适合对稀有事件进行分类；
3. 特别适合于多分类问题(multi-modal,对象具有多个类别标签)， kNN比SVM的表现要好。
4. 懒惰算法，对测试样本分类时的计算量大，内存开销大，评分慢；
5. 当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数；
6. 可解释性较差，无法给出决策树那样的规则。

1.2.2              缺点

1.3 常见问题

1.3.1              k值的设定

k值选择过小，得到的近邻数过少，会降低分类精度，同时也会放大噪声数据的干扰；而如果k值选择过大，并且待分类样本属于训练集中包含数据数较少的类，那么在选择k个近邻的时候，实际上并不相似的数据亦被包含进来，造成噪声增加而导致分类效果的降低。

如何选取恰当的K值也成为KNN的研究热点。k值通常是采用交叉检验来确定（以k=1为基准）。

经验规则：k一般低于训练样本数的平方根。

1.3.2              类别的判定方式

投票法没有考虑近邻的距离的远近，距离更近的近邻也许更应该决定最终的分类，所以加权投票法更恰当一些。

1.3.3              距离度量方式的选择

高维度对距离衡量的影响：众所周知当变量数越多，欧式距离的区分能力就越差。

变量值域对距离的影响：值域越大的变量常常会在距离计算中占据主导作用，因此应先对变量进行标准化。

1.3.4              训练样本的参考原则

学者们对于训练样本的选择进行研究，以达到减少计算的目的，这些算法大致可分为两类。第一类,减少训练集的大小。KNN算法存储的样本数据,这些样本数据包含了大量冗余数据,这些冗余的数据增了存储的开销和计算代价。缩小训练样本的方法有:在原有的样本中删掉一部分与分类相关不大的样本样本,将剩下的样本作为新的训练样本;或在原来的训练样本集中选取一些代表样本作为新的训练样本；或通过聚类,将聚类所产生的中心点作为新的训练样本。

在训练集中，有些样本可能是更值得依赖的。可以给不同的样本施加不同的权重，加强依赖样本的权重，降低不可信赖样本的影响。

1.3.5              性能问题

kNN是一种懒惰算法，而懒惰的后果：构造模型很简单，但在对测试样本分类地的系统开销大，因为要扫描全部训练样本并计算距离。

已经有一些方法提高计算的效率，例如压缩训练样本量等。

1.4 算法流程

1. 准备数据，对数据进行预处理
2. 选用合适的数据结构存储训练数据和测试元组
3. 设定参数，如k
4. 维护一个大小为k的的按距离由大到小的优先级队列，用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组，分别计算测试元组到这k个元组的距离，将训练元组标号和距离存入优先级队列
5. 遍历训练元组集，计算当前训练元组与测试元组的距离，将所得距离L 与优先级队列中的最大距离Lmax
6. 进行比较。若L>=Lmax，则舍弃该元组，遍历下一个元组。若L < Lmax，删除优先级队列中最大距离的元
7. 组，将当前训练元组存入优先级队列。
8. 遍历完毕，计算优先级队列中k 个元组的多数类，并将其作为测试元组的类别。

      9.测试元组集测试完毕后计算误差率，继续设定不同的k 值重新进行训练，最后取误差率最小的k 值。

Java代码实现

public class KNN {
    /**
     * 设置优先级队列的比较函数，距离越大，优先级越高
     */
    private Comparator<KNNNode> comparator =new Comparator<KNNNode>(){
        public int compare(KNNNode o1, KNNNode o2) {
            if (o1.getDistance() >= o2.getDistance())
                return -1;
            else
                return 1;
        }
    };
    /**
     * 获取K个不同的随机数
     * @param k 随机数的个数
     * @param max 随机数最大的范围
     * @return 生成的随机数数组
     */
    public List<Integer> getRandKNum(int k, int max) {
        List<Integer> rand = new ArrayList<Integer>(k);
        for (int i = 0; i < k; i++) {
            int temp = (int) (Math.random() * max);
            if (!rand.contains(temp))
                rand.add(temp);
            else
                i--;
        }
        return rand;
    }

 /* 计算测试元组与训练元组之前的距离
     * @param d1 测试元组
     * @param d2 训练元组
     * @return 距离值
     */
    public double calDistance(List<Double> d1, List<Double> d2) {
        double distance = 0.00;
        for (int i = 0; i < d1.size(); i++)
            distance += (d1.get(i) - d2.get(i)) *(d1.get(i)-d2.get(i));
        return distance;
    }
    
    /**
     * 执行KNN算法，获取测试元组的类别
     * @param datas 训练数据集
     * @param testData 测试元组
     * @param k 设定的K值
     * @return 测试元组的类别
     */
    public String knn(List<List<Double>> datas, List<Double> testData,             int k) {
        PriorityQueue<KNNNode> pq = new PriorityQueue<KNNNode>                                                     (k,comparator);
        List<Integer> randNum = getRandKNum(k, datas.size());
        for (int i = 0; i < k; i++) {
            int index = randNum.get(i);
            List<Double> currData = datas.get(index);
            String c = currData.get(currData.size() - 1).toString();
            KNNNode node = new KNNNode(index, calDistance(testData,                                         currData), c);
            pq.add(node);
        }
        for (int i = 0; i < datas.size(); i++) {
            List<Double> t = datas.get(i);
            double distance = calDistance(testData, t);
            KNNNode top = pq.peek();
            if (top.getDistance() > distance) {
                pq.remove();
                pq.add(new KNNNode(i, distance, t.get(t.size() - 1).                                     toString()));
            }
        }
        return getMostClass(pq);
}

 

/**
     * 获取所得到的k个最近邻元组的多数类
     * @param pq 存储k个最近近邻元组的优先级队列
     * @return 多数类的名称
     */
    private String getMostClass(PriorityQueue<KNNNode> pq) {
        Map<String, Integer> classCount=new HashMap<String,Integer>();
        int pqsize = pq.size();
        for (int i = 0; i < pqsize; i++) {
            KNNNode node = pq.remove();
            String c = node.getC();
            if (classCount.containsKey(c))
                classCount.put(c, classCount.get(c) + 1);
            else
                classCount.put(c, 1);
        }
        int maxIndex = -1;
        int maxCount = 0;
        Object[] classes = classCount.keySet().toArray(); 
        for (int i = 0; i < classes.length; i++) { 
            if (classCount.get(classes[i]) > maxCount)
                maxIndex = i; maxCount = classCount.get(classes[i]);
        } 
        return classes[maxIndex].toString();
    }
}